
3058
.pdfМинистерство образования и науки Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Воронежская государственная лесотехническая академия»
МАТЕМАТИКА
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ
Методические указания к выполнению лабораторных работ для студентов специальностей
080109 – Бухгалтерский учет, анализ и аудит,
080102 – Мировая экономика
Воронеж 2010
2
УДК 519.87+65в631
Раецкая, Е. В. Математика. Экономико-математические методы и модели [Текст] : методические указания к выполнению лабораторных работ для студентов специальностей 080109 – Бухгалтерский учет, анализ и аудит, 080102
– Мировая экономика / Е. В. Раецкая ; М-во образования и науки РФ, ГОУ ВПО
«ВГЛТА». – Воронеж, 2010. – 28 с.
Печатается по решению учебно-методического совета ГОУ ВПО «ВГЛТА» (протокол № 2 от 9 октября 2009 г.)
Рецензент канд. физ.-мат. наук, доц. кафедры математики ВАИУ Т.В. Перловская

3
Под экономико-математической моделью понимается система математических соотношений, используемых для воспроизведения и исследования свойств объектов, явлений и процессов, встречающихся в экономике.
Прогресс в области прикладной математики в XX веке (теория игр, математическая статистика, математическое программирование) обусловил развитие микро- и макроэкономики и прикладных экономических дисциплин.
Основы математического моделирования были заложены Ф. Кене (1758 г., «Экономические таблицы»), А. Смитом (классическая макроэкономическая модель), Д. Рикардо (модель международной торговли). В XIX веке закладывались основы математического подхода к исследованию рыночной экономики (Л. Вальрас, О. Курно, В. Парето, Ф. Эджворт).
В XX веке математическое моделирование экономических процессов
получило широкое |
развитие благодаря |
трудам В. |
Леонтьева, Д. Хикса, |
Р. Солоу, П. Cамуэльсона, Е.Е. Слуцкого, В.С. Новожилова, Л.В. Канторовича. |
|||
Производственные функции |
|
|
|
Определение 1. |
Производственная |
функция |
(ПФ) – это функция, |
независимая переменная которой имеет смысл объёма используемого в данном производстве ресурса, а значение функции – объем выпускаемой продукции. Независимую переменную еще называют фактором.
Производственная функция y = f(x) , где х ≥0, у≥0, является функцией одной переменной (фактора) и называется однофакторной.
Производственная функция y = f (x1,..., xn ) , xi ≥ 0 , y ≥ 0 (i =1, n) является функцией нескольких переменных (факторов) и называется многофакторной. В дальнейшем ограничимся случаем двухфакторных ПФ.
Производственные функции предназначены для моделирования процесса производства отдельной фирмы, отрасли, или даже экономики государства. Единицами измерения затрачиваемых ресурсов и значений могут служить и натуральные и стоимостные показатели.
Производственная функция называется статической, если сама функция и её параметры не зависят от времени и динамической, если параметры функции зависят от времени или время входит в функцию в качестве независимой переменной y = f (x1,..., xn ,t) .
4
Основными видами производственных функций являются:
1. Линейная производственная функция y = a0 +a1x1 +a2 x2 .
2. Мультипликативная ПФ |
y = a xα1 xα2 . |
||
|
0 |
1 |
2 |
Можно перейти от мультипликативной к линейной ПФ при помощи логарифмирования ln y = ln a0 +a1 ln x1 +a2 ln x2 .
Обозначая ln y = z , ln x1 = u , ln x2 = v2 , ln a0 = b , получаем линейную ПФ z = b + a1u + a2 v .
Типичным примером мультипликативной ПФ является функция КоббаДугласа, которая была представлена Ч. Коббом и П. Дугласом в 1928 г. на основе данных по обрабатывающей промышленности США за период 1899 –
1922 гг. в виде y = a Kα1 |
Lα2 |
, |
0 |
|
|
где a0 - расчетный индекс производства;
К – индекс основного капитала (объем используемого капитала); L – индекс занятости (затраты труда).
ПФ Кобба-Дугласа получила широкое распространение в экономических приложениях благодаря структурной простоте. Её можно представить в общем
виде y = a xα1 xα2 |
, где |
a - коэффициент, учитывающий влияние факторов, |
||
0 |
1 |
2 |
|
0 |
которые определяются на основе статистических данных с помощью корреляционных методов.
Производственная функция Кобба-Дугласа устанавливает зависимость между величиной суммарного общественного продукта от совокупных затрат живого
труда |
x1 и суммарного объёма применяемых производственных фондов x2 . |
|||||||||||
Наблюдаются |
следующие |
закономерности, |
согласно |
результатам |
||||||||
статистических данных: |
0 <α1 <1 , 0 <α2 <1, |
α1 <α2 . |
|
|
||||||||
Обозначим α1 +α2 = P . |
|
Увеличение ресурсов в |
k |
раз даёт |
новое значение |
|||||||
объёма производства y =α |
0 |
(kx )α1 |
(kx )α2 =α |
kα1 +α2 x α1 xα2 . |
|
|
||||||
|
|
|
|
1 |
2 |
0 |
|
1 |
2 |
|
|
|
Если |
М = 1, то увеличение ресурсов в |
|
k |
раз приводит к увеличению объёма |
||||||||
производства |
также в |
k |
раз. |
То есть, чтобы удвоить объем выпускаемой |
||||||||
отраслью продукции в 2 раза, |
необходимо удвоить число предприятий этой |
|||||||||||
отрасли. |
|
|
|
|
|
|
|
|
|
|
|
|
Если |
P <1, |
то имеется |
отрицательный |
эффект |
расширения производства |
|||||||
(увеличение ресурсов опережает увеличение выпуска).
5
Если P >1, то имеется положительный эффект расширения производства (увеличение выпуска опережает увеличение ресурсов).
Основные свойства производственных функций
1.При отсутствии хотя бы одного производственного ресурса производство невозможно, то есть y = f (0; x2 ) = f (x1 ;0) = 0 .
2.С увеличением объема использования любого ресурса объём выпуска растет:
при x11 < x12 верно f (x11 ; x2 ) < f (x12 ; x2 ) ;
при x12 < x22 верно f (x1 ; x12 ) < f (x1 ; x22 ) .
3.Рост использования ресурсов приводит к росту результата производства: при
x > 0 |
(i =1, 2) выполнено |
∂f |
> 0 . С ростом потребления одного из ресурсов, |
|
|||
i |
|
∂xi |
|
|
|
||
при неизменном объёме другого ресурса, объём выпуска возрастает.
4. Закон убывающей эффективности или закон «всё меньшей отдачи» с
ростом производства: при |
x > 0 |
(i =1, 2) верно |
∂2 f |
> 0 . |
|
i |
|
∂x 2 |
|
|
|
|
i |
|
С ростом объёма затрат одного из ресурсов, при неизменном объёме использования другого ресурса, величина прироста выпуска на каждую дополнительную единицу i-го ресурса не увеличивается.
То есть, начиная с некоторого объёма затрат ресурсов, их дальнейшее увеличение становится нерентабельным.
Каждый из ресурсов x1 и x2 характеризуется средней и предельной величиной. (Далее эти величины будем рассчитывать на примере ПФ КоббаДугласа).
1. Средней производительностью i-го ресурса или средним выпуском по i-
му ресурсу, называется величина |
A = |
f (x1 ; x2 ) |
, i =1, 2 . |
|
||||
|
|
|||||||
|
|
x |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Средняя производительность труда A = |
y |
=α |
|
xα1 −1 xα2 |
||||
|
0 |
|||||||
|
|
1 |
x1 |
1 |
2 |
|||
|
|
|
|
|
|
|||
показывает, сколько единиц выпускаемой продукции приходится на единицу затрачиваемого труда.
Для ПФ Кобба-Дугласа A =α |
0 |
xα1 −1 xα2 . |
|
1 |
1 |
2 |
|
6
С увеличением затрат труда средняя производительность снижается, так как показатель степени α1 −1 является отрицательной величиной.
Средняя фондоотдача A2 |
= |
f (x1 ; x2 ) |
характеризует объём продукции в расчете |
|||
|
||||||
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
на единицу используемых производственных фондов. |
||||||
Для ПФ Кобба-Дугласа A |
=α |
0 |
xα1 |
xα2 −1 . |
||
2 |
|
|
1 |
2 |
|
|
2.Предельной (маржинальной) производительностью i-го ресурса или
предельным выпуском по i-му ресурсу, называется первая частная
производная M |
i |
= |
|
∂f |
|
, i =1, 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разностный аналог этой формулы имеет вид Mi ≈ |
|
f , |
i =1, 2 . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
Предельная |
|
производительность |
|
труда |
|
|
|
показывает, |
сколько |
|||||||||||||
дополнительных единиц продукции приносит дополнительная единица |
||||||||||||||||||||||
труда Mi = lim |
|
f |
= |
|
∂y |
. Для ПФ Кобба-Дугласа |
|
M1 |
=α0α1 x1α1 −1 x2α2 . |
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
x→0 |
|
x1 |
∂x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдём вторую частную производную |
∂2 f |
= a α |
(α |
|
|
α −2 |
x |
α |
2 , которая, в силу |
|||||||||||||
∂x 2 |
1 |
−1)x 1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 1 |
|
|
|
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
α1 −1 < 0 , |
является |
отрицательной |
величиной. |
|
Следовательно, |
предельная |
||||||||||||||||
производительность с ростом |
x1 уменьшается. |
|
|
|
|
|
|
|
|
|
||||||||||||
Сравнивая выражения для |
M1 |
и A1 , |
получаем M1 =α1 A1 , то есть для ПФ Кобба- |
|||||||||||||||||||
Дугласа |
предельная |
производительность |
|
|
|
всегда |
|
|
ниже |
средней |
||||||||||||
производительности, в силу того, что |
0 <α1 |
<1 . |
|
|
|
|
|
|
|
|
|
|||||||||||
Предельная фондоотдача определяется как частная производная выпуска
продукции по объёму фондов |
M |
|
= |
∂y |
. |
||
2 |
|
||||||
|
|
|
|
|
∂x |
||
|
|
|
|
|
|
2 |
|
Для ПФ Кобба-Дугласа |
M 2 = a0α2 x1α1 x2α2 −1 . |
||||||
Сравнивая выражения |
для |
M1 |
|
и |
A1 , получаем M2 =α2 A2 , то есть для ПФ |
||
Кобба-Дугласа |
предельная фондоотдача всегда ниже средней фондоотдачи, в |
||||||
силу того, что |
0 <α2 <1. |
|
|
|
|
|
|

7
3. Эластичностью выпуска по i-му ресурсу (частной эластичностью выпуска) называется отношение предельной производительности i-го ресурса
к его средней производительности |
Ei |
= |
Mi |
= |
xi |
|
∂f |
, |
i =1, 2 . |
A |
f (x ; x ) ∂x |
||||||||
|
|
|
i |
|
1 2 |
|
i |
|
|
(В математике эластичность - это отношение относительного прироста функции (зависимой переменной) к относительному приросту аргумента (независимой переменной).)
Эластичность выпуска по i-му ресурсу показывает на сколько процентов изменится объём выпускаемой продукции, при изменении затрат этого ресурса на 1 процент.
Часто используется разностный аналог этой формулы Ei ≈ |
f |
x1 . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Эластичность выпуска продукции по затратам труда для |
ПФ Кобба-Дугласа |
|||||||||||||
имеет вид |
E1 =α1 , а эластичность выпуска по фондам имеет вид E2 =α2 . |
|
||||||||||||
Таким образом, показатели степеней |
|
α1 |
и |
α2 |
в ПФ Кобба-Дугласа |
имеют |
||||||||
смысл частных эластичностей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина |
E = E1 + E2 называется эластичностью производства или полной |
|||||||||||||
эластичностью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Технологической или предельной нормой замены |
|
i-го ресурса j-м |
||||||||||||
ресурсом называется величина |
R = |
∂f |
|
/ |
∂f |
|
или |
R |
= |
Ei xj |
|
( i =1, 2 ), |
которая |
|
∂x |
|
∂x |
|
E x |
|
|||||||||
|
|
ij |
|
|
j |
|
ij |
|
|
|
|
|||
|
|
|
i |
|
|
|
|
j i |
|
|
|
|||
показывает как изменится объём выпуска, если единицу одного ресурса заменить единицей другого ресурса.
Для ПФ Кобба-Дугласа |
R12 |
= |
α1 x2 |
и R21 |
= |
|
α2 x1 |
. |
|||
α |
|
x |
|
||||||||
|
|
|
2 |
|
|
α x |
|||||
|
|
|
|
1 |
|
|
1 |
2 |
|
||
Для линейной функции средние, предельные значения, эластичности и нормы замены имеют вид
A |
= |
|
f (x) |
= |
a0 |
|
+ a |
+ |
a2 x2 |
, |
A = |
|
|
f (x) |
|
= |
a0 |
+ a |
+ |
a1 x1 |
, M |
|
= |
|
∂f |
= a , |
M |
|
= |
∂f |
|
= a |
, |
||||||||||
|
x |
|
x |
x |
|
|
|
x2 |
x |
|
x |
|
|
∂x |
|
∂x |
|||||||||||||||||||||||||||
1 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
1 |
|
|
2 |
|
|
|
2 |
||||||||||||||
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|||||||
E |
= |
M1 |
= |
a |
|
|
|
|
|
|
, E |
|
|
= |
M |
2 |
= |
a |
|
|
|
|
|
|
|
, |
R = |
a1 |
, |
R = |
a2 |
. |
|||||||||||
|
|
|
1 |
|
a0 |
|
|
|
a2 x2 |
|
|
|
|
|
2 |
a0 |
|
|
|
a1 x1 |
|
|
|
|
|||||||||||||||||||
|
A |
|
|
|
|
|
|
A |
|
|
|
|
a |
a |
|||||||||||||||||||||||||||||
1 |
|
|
|
( |
+ a1 + |
) |
2 |
|
|
|
|
( |
|
+ a2 + |
) |
12 |
|
|
21 |
|
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
x1 |
|
|
|
|
x1 |
|
|
|
|
|
|
|
x2 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||

8
Функции полезности
Рассмотрим индивида-потребителя, который потребляет некоторые блага. В качестве благ могут рассматриваться:
-продукты питания;
-платные услуги;
-товары первой необходимости;
-предметы роскоши и т.д.
Пусть имеется два вида благ и количество потребления каждого блага равно xi (i =1, 2) , то есть рассматривается набор благ x = (x1 ; x2 ) . Полагают, что каждый потребитель принимает решение о потреблении, покупках и т.д., самостоятельно, то есть он сам решает какой из наборов x , y или z для него более желателен. На множестве потребительских наборов определена функция u(x) = u(x1; x2 ) , которая называется функцией полезности потребителя или
целевой функцией потребительского предпочтения.
Если функция полезности дифференцируема, то она имеет следующие свойства:
1. |
∂u |
= u ′ > 0 (i =1, 2) . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
∂xi |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если x1 |
> x2 |
, то u(x1 ; x ) > u(x2 |
; x |
2 |
) , при x |
= const ; |
|||||
1 |
1 |
|
1 |
2 |
1 |
|
|
2 |
|
||
если x1 |
> x2 |
, то u(x ; x1 ) < u(x ; x |
2 ) , при |
x |
= const , |
||||||
2 |
2 |
|
1 |
2 |
1 |
2 |
|
1 |
|
||
то есть возрастание потребления одного продукта, при неизменном потреблении другого, приводит к росту потребительской оценки.
Первые частные производные функции полезности называются
предельными полезностями продуктов.
Закон Госсена |
∂2u |
= u ′′ < 0 |
(i =1, 2) , |
|
∂x2 |
ii |
|
|
i |
|
|
то есть предельная производительность любого товара уменьшается с ростом
его потребления. |
|
|
||
2. |
∂2u |
= u ′′ |
> 0 , |
(i ≠ j;i, j =1, 2) . Это свойство означает, что предельная |
|
||||
|
|
ij |
|
|
|
∂xi ∂xj |
|
|
|
полезность каждого продукта увеличивается с ростом другого продукта.
9
Можно привести несколько видов функций полезности, удовлетворяющих
всем указанным выше свойствам: |
|
|
||||||||
1. |
Неоклассическая |
u(x ; x ) = xα xβ , |
α, β > 0 , |
α + β <1 . |
||||||
|
|
1 |
2 |
1 |
2 |
|
|
|||
|
|
|
|
|
|
2 |
|
2 |
2 |
|
2. |
Квадратическая u( |
|
|
= ∑ai xi |
+∑∑bij xi xj . |
|
||||
x) |
|
|||||||||
|
|
|
|
|
|
i=1 |
|
i=1 j=1 |
|
|
3. |
Логарифмическая |
u( |
|
= ∑2 |
ai |
log(xi −bi ) , ai > 0 , |
xi >bi ≥ 0 . |
|||
x) |
||||||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
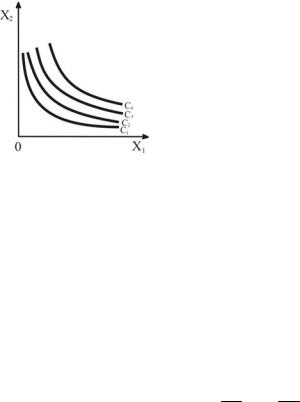
Кривые безразличия Кривая безразличия – это кривая, соединяющая потребительские наборы с
одним и тем же уровнем потребления потребностей. |
Кривые безразличия |
|
представляют собой линии уровня функции полезности |
u =u(x1; x2 ) . |
|
Уравнение кривой безразличия |
u(x1; x2 ) =C . Множество кривых безразличия |
|
изображается на плоскости X1OX2 |
в виде семейства кривых. |
|
Их характерный вид приведен на рис. 1.
Рис. 1
Основные свойства кривых безразличия:
1.Кривые безразличия, соответствующие разным уровням удовлетворения потребностей не пересекаются и не касаются.
2.Кривые безразличия убывают.
Представим уравнение |
для кривой безразличия в виде x2 =ϕ(x1 ) , то есть |
выразим x2 из выражения |
u =u(x1; x2 ) . Дифференциал функции вдоль линии |
уровня равен нулю du = ∂u dx1 + ∂u dx2 = 0 ,
∂x1 ∂x2
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
dx |
u ′ |
|
|
|
|
|
|
|||
откуда |
следует, что |
2 |
= − |
1 |
, |
то |
есть первая |
производная функции |
|||||
|
|
|
|||||||||||
|
|
|
dx1 |
u2′ |
|
|
|
|
|
|
|||
x2 =ϕ(x1 ) , отрицательна (в силу свойства 1 функции полезности). |
|||||||||||||
3. Кривые безразличия выпуклы вниз. |
|
|
|
||||||||||
|
|
|
|
|
|
dx |
|
u ′ |
x |
u ′ |
|||
Разностный аналог формулы |
|
2 |
= − |
1 |
имеет вид |
2 ≈ − |
1 |
. |
|||||
|
|
|
|
|
|
dx1 |
|
u2′ |
x1 |
u2′ |
|||
Величина |
− x2 |
называется нормой замены первого продукта вторым, она |
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
показывает, на сколько нужно увеличить (уменьшить) потребление второго продукта, при уменьшении (увеличении) потребления первого продукта, чтобы
уровень потребления остался прежним. |
Величина |
dx2 |
называется |
|
dx |
||||
|
|
|
||
|
|
1 |
|
предельной нормой замены первого продукта вторым.
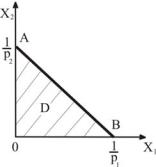
Задача потребительского выбора
Если обозначить цену на каждое благо через P = ( p1; p2 ) , а совокупный доход потребителя через J , то можно получить бюджетное ограничение p1x1 + p2 x2 ≤ J .
Множество наборов товаров (x1; x2 ) стоимостью J называется бюджетным множеством и на плоскости X1OX2 представляется в виде множества D точек плоскости, ограниченного треугольником ОАВ (см. рис. 2).
Рис. 2
