Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2099.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

3.05 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

2. РАСЧЁТ ОДНОФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

2.1. Основные понятия, параметры и зависимости

С
2.1.1. Способы представления синусоидальных величин
Мгновенное значение синусоидально изменяющейся с течением
времени вел ч ны [1, 2, 3, 5, 6],
значение
	a(t) = Am sin(ωt + ψa ),							(2.1)
где Am – макс мальное		или амплитуда; (ωt + ψa ) – фаза; ψa –
начальная фаза; ω – угловая частота, рад/с.
Пер од Т (с), угловая частота ω и частота f (Гц) связаны соот-
ношен ем [5, 6]:
	ω = 2πf	=	2π	; f	=	1	.	(2.2)
	ω = 2πf	=		; f	=		.	(2.2)
			T		T
	А

Аналитическоебпредставление синусоидальных функций неудобно при расчётах, т.к. приводит к громоздким тригонометрическим выражениям. Поэтому при анализе цепей переменного тока эти

функции представляют в виде векторов, что позволяет перейти от
тригонометрических к алгебраическим выражениям и, кроме того,
				Д
получить наглядное представление о количественных и фазовых со-
отношениях величин [1, 2, 3, 5, 6].
а	ω	б			в	•
Y						•
Y		Am			И
		Am			+j	Am
	ψa			a(t)		ψa Am sin ψa
	ψa					ψa Am sin ψa
0	X	0	π 2	π	ωt 0		+1
0	X	0	π 2	π	ωt 0	Am cosψa	+1
		ψa				Am cosψa

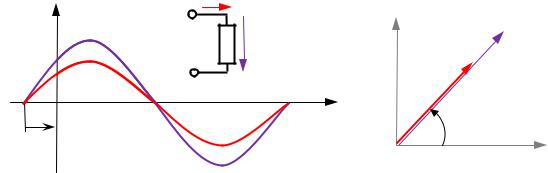
Рис. 2.1. Способы представления синусоидальной величины:

а– вращающимся вектором; б – график изменения величины по фазе;

в– на комплексной плоскости

Произвольная синусоидальная функция времени (рис. 2.1, б) соответствует проекции на ось OY вектора с модулем, равным Am, вращающегося на плоскости XOY с постоянной угловой скоростью ω из

начального положения, составляющего угол ψa с осью OX (рис. 2.1, а). Если таким же образом на плоскости изобразить несколько векторов, соответствующих разным синусоидальным функциям, имеющим одинаковую частоту, то они будут вращаться совместно, не меняя взаимного положения, которое определяется только начальной фазой этих функций. Поэтому при анализе цепей, в которых все функции имеют одинаковую частоту, её можно исключить из параметров, ограничившись амплитудой и начальной фазой. В этом случае векторы, изображающ е с нусоидальные функции, будут неподвижными

(рис. 2.1, в).

Метод представления синусоидальных функций времени изо-
С
бражен	в в де векторов на комплексной плоскости (см. рис. 2.1, в)

называется с мвол ческим методом или методом комплексных ам-

ямиm

плитуд [1, 2, 3, 5, 6].

алгебра

Комплексное ч сло, соответствующее точке, в которой находит-

ся конец вектора A , может

ыть записано в следующих формах:

ческой:

= p

+ jq

(cosψ

+ j sin

);

(2.3)

показательной:

jψa

A e

(2.4)

;

где p – вещественная часть комплексного числа

Re[A

], p = A cosψ

q – мнимая часть комплексного числа Im[A

q = A sinψ

; j – мни-

мая единица или оператор поворота на угол π/2 = 90°,

j =

−1

= e

2 ;

Am – модуль комплексного числа

;

+ q2

(2.5)

ψa – угол или аргумент комплексного числа,

arctg

при p > 0,q > 0;

при p < 0,q < 0;

ψa = arctg

+180

(2.6)

при p < 0,q > 0.

arctg

−180

В соответствии с формулой Эйлера [1, 2, 3, 5, 6]:

e jψa

= cosψa + j sin ψa .

(2.7)

Комплексное число

, модуль которого равен амплитуде си-

нусоидальной функции, называется комплексной амплитудой. Но ам-

плитуда и действующее значение синусоидальной функции связаны

соотношением A = Am

, поэтому расчёт можно вести сразу для

действующ х значен й, если использовать комплексные числа с со-

ответствующ м модулем

= A

. Число

называется комплекс-

ПрименКомплексное ч сло A = p − jq = Ae− jψa

называется сопряжён-

ным действующ м значением или просто комплексным значением.

тельно к ЭДС, напряжению и току такие комплексные вели-

чины ( E,U , I ) называют просто комплексной ЭДС, комплексным на-

пряжен ем

комплексным током.

jψa

ным ч слу A = p + jq =

Например, для синусоидального тока, определяемого тригоно-

метрическимбвыражением

i = 5

sin(314t − 30 ),

комплексное значение

− j30

= 5e

;

5cos30

− j5sin 30 =

3 2

− j 5 2

комплексно-сопряжённое значение

j30

= 5e

= 5 3 2 + j 5 2 .

Алгебраическая форма представления удобна для сложения

комплексных чисел,

+ A

(p + p

)+ j(q + q

(2.8)

а показательная – для умножения и деления:

(ψ

+ψ

)

j(ψ

−ψ

)

= A A e

;

(2.9)

2.1.2. Закон Ома для резистивного, индуктивного
	и ёмкостного элементов
Зависимости между токами и напряжениями резистивных, ин-
дуктивных и ёмкостных элементов определяются происходящими в
них физическими процессами. При анализе цепи переменного тока
необходимо рассматривать амплитудные и фазовые отношения между
токами и напряжениями [1, 2, 3, 5, 6].
Для мгновенных значений напряжения и тока в резистивном
элементе справедл во соотношение, определяемое законом Ома [5]:
С		uR = RiR ,
С
uR = RIRm sin(ωt + ψi ) = URm sin(ωt + ψu ),						(2.10)
где ампл туды тока	напряжения связаны соотношением
илиURm = RIRm ,						(2.11)
а их начальные фазы од наковые:
		ψu = ψi ,				(2.12)
т.е. ток и напряжениебв резистивном элементе изменяются синфазно –
совпадают по фазе, как показано на рис. 2.2, а для начальной фазы
ψu = ψi > 0.
а	I∙R			б
uR, iR	А					∙
uR, iR		.				∙
uR	R	UR	+j	∙	UR
				IR
iR		Д
0		Д
0		ωt		ψu		= ψi
ψu = ψi				ψu		= ψi
ψu = ψi			0			+1
			0			+1
Рис. 2.2. Цепь синусоидального тока с резистивным элементом:
а – графики изменения напряженияИ, тока;
б – векторная диаграмма на комплексной плоскости

Действующие значения напряжения UR	и тока IR связаны
законом Ома [5]:
UR = RIR .	(2.13)

Представив синусоидальные ток и напряжение резистивного

элемента соответствующими комплексными значениями

IR = IRe jψi

и UR = URe jψu ,

получим закон Ома для резистивного элемента в комплексной форме

UR = RIR .

(2.14)

оотношение между комплексными значениями тока и напря-

жения для рез ст вного элемента наглядно иллюстрируется вектор-

ной диаграммой элемента (рис. 2.2, б).

появится

Если в ндукт вном элементе ток синусоидальный

iL = ILm sin(ωt + ψi ),

(2.15)

то по закону электромагнитной индукции на индуктивном элементе

напряжен е [5]:

uL = L

L = ωLILm cos(ωt + ψi )=ULm sin

ωt + ψi

=ULm sin(ωt + ψu ), (2.16)

А2

где амплитуды тока и напряжения связаны соотношением

U Lm = ωLILm ,

(2.17)

а их начальные фазы – соотношением

Дπ

= ψ

+ π .

(2.18)

На рис. 2.3, а показан график мгновенных значений синусоидальных тока и напряжения индуктивного элемента для ψi > 0, из ко-

торого видно, что напряжение опережает ток по фазе на угол
ϕ = ψu − ψi =		2	.	(2.19)
Величина

X L = ωL = 2πfL				(2.20)
называется индуктивным сопротивлением [ОмИ], а обратная величина
BL =	1			(2.21)
	ωL

– индуктивной проводимостью [См] [5].

Значения величин XL и BL являются параметрами индуктивных элементов цепей синусоидального тока.

	а	I∙L		б
uL, iL		XL	.
	iL	XL	UL	+j	I∙L
С			U∙	L	I∙L
С			ωt	ψu
	0	uL		ψu	ψi
φ = π/2	0	uL
φ = π/2	ψi
ψu				0	+1

синусоР с. 2.3. Цепь переменного тока с индуктивным элементом: а – графики изменения напряжения, тока;

б – векторная диаграмма на комплексной плоскости

Индукт вное сопротивление пропорционально угловой частоте дального тока, при постоянном токе (ω = 0) оно равно нулю.

По этой пр ч не электротехнические устройства, предназначенные для работы в цепи переменного тока, нельзя включать в цепь посто-

янного тока [5].
Действующиебзначения тока IL и напряжения UL на участке цепи
переменного тока с реактивным индуктивным сопротивлением ХL
связаны по закону Ома [5]:
				U L = X L IL .							(2.22)
	А
Представив синусоидальные ток и напряжение индуктивного
элемента соответствующими комплексными значениями
	I	= I	L	e jψi и U	L	= U	L		e jψu ,
	L		L		L		L
получим закон Ома для индуктивногоДэлемента в комплексной форме
							+	π
						j ψi	+				(2.23)
	UL = X LILe jψu = X LILe							2		= jX LIL .	(2.23)

Входящая в это выражение величинаИjXL = jωL называется

комплексным сопротивлением индуктивного элемента, а обратная ей величина 1/(jωL) = – jBL – комплексной проводимостью индуктивного элемента [5].

Соотношение между комплексными значениями тока и напряжения для индуктивного элемента наглядно иллюстрируется векторной диаграммой элемента (рис. 2.3, б).

Комплексное значение напряжения на индуктивном элементе можно выразить и через комплексное значение потокосцепления

Ψ = LIL .

(2.24)

Тогда выражение (2.23) примет вид

UL = −EL = jωΨ .

(2.25)

Полученное уравнение представляет закон электромагнитной

индукц

в комплексной форме.

Если напряжен е между выводами ёмкостного элемента изме-

синусоdt

няется по с нусо

дальному закону

uC = UCm sin(ωt + ψu ),

(2.26)

то

дальный ток [5]:

i = C

= ωCU

cos(ωt + ψ

)= I

sin ωt + ψ

= I

sin(ωt + ψ

), (2.27)

где ампл туды тока напряжения связаны соотношением

ICm

= ωCUCm

(2.28)

а начальные фазы – соотношением

ψi

= ψu

+ π .

(2.29)

Дπ

На рис. 2.4,

а показан график мгновенных значений синусои-

дальных тока и напряжения ёмкостного элемента для ψu > 0, из которого видно, что напряжение отстаёт от тока по фазе на угол π/2, т.е. сдвиг по фазе между напряжением и током

ϕ = ψu − ψi			= −	2	.	(2.30)
				2
Величина
X С =	1	=	1			(2.31)
X С =		=				(2.31)
	ωC 2πfC					И
	ωC 2πfC
называется ёмкостным сопротивлением [Ом], а обратная величина
BC = ωC						(2.32)

– ёмкостной проводимостью [См] [5].

Значения величин XС и BС являются параметрами ёмкостных элементов цепей синусоидального тока.

В противоположность индуктивному сопротивлению ёмкостное

сопротивление уменьшается с увеличением частоты синусоидального

тока. При постоянном напряжении ёмкостное сопротивление беско-

нечно велико. Поэтому конденсатор, подключенный в цепь постоян-

ного тока, ток не пропускает [5].

I∙C

u , iC

∙

φ = –π/2 ψu

ωt

ψi

ψu

ψi

Рис. 2.4. Цепь переменного тока с ёмкостным элементом:

а – графики изменения напряжения, тока;

б – векторная диаграмма на комплексной плоскости

Действующие значения тока IС и напряжения UС на участке цепи

переменного тока с реактивным ёмкостным сопротивлением ХС свя-

заны по закону Ома [5]:

= X C IC .

(2.33)

ωC

Представив синусоидальные ток и напряжение ёмкостного эле-

мента соответствующими комплексными значениями

IC = IC e jψi

и UC = UC e jψu ,

получим закон Ома для ёмкостного элемента в комплексной форме

ψi −

UC = X C IC e jψu

= X C IC e

= − jX C IC .

(2.34)

Величина – jXС = 1/(jωС) называется комплексным сопротивлением ёмкостного элемента, а обратная ей величина jωС = jBС – комплексной проводимостью ёмкостного элемента [5].

2.1.3. Пассивный двухполюсник в цепи синусоидального тока

Параметром пассивного элемента цепи синусоидального тока

(рис. 2.5)

является комплексное сопротивление Z = Ze jϕ

– комплекс-

ное число, равное отношению комплексного напряжения на зажимах

данного элемента к комплексному току этого элемента [5, 6],

Z =

= R + jX

= Ze

jϕ

(2.35)

где R – вещественная часть комплексного сопро-

вления

Z , или активное сопротивление; X –

часть Z , или реактивное сопротивление

u, U

цепи, составленное из индуктивного и ёмкостно-

го

сопротивлений,

X = X L − X C ;

Z – модуль

комплексного сопротивления, или полное со-

мнимая

Z =

R2 + X 2 ;

ϕ –

аргумент Z ,

Рис. 2.5. Пассивный

противление,

элемент

равный углу сдвига фаз между током и напря-

жением (ϕ = ψ

− ψ

ϕ = arctg X .

Отношение комплексного тока в данной цепи к комплексному

напряжению на её зажимах называется комплексной проводимостью

электрической цепи [5, 6]:

АI − jϕ 1

(2.36)

= G

− jB

= Ye

где G

–

активная

проводимость;

В –

реактивная проводимость,

B = B

− B ; Y – полная проводимость,

Y =

G2 + B2 ; ϕ = arctg B .

От

комплексного

сопротивления

можно

всегда перейти к

комплексной проводимости Y , пользуясь соотношениями

R =

;

X =

= B ;

(2.37)

+ B

G =

;

B =

= X .

(2.38)

R2 + X 2

Z 2

R2 + X 2

Z 2

Закон Ома для участка цепи синусоидального тока имеет вид

U = I Z = I Y .

(2.39)

2.1.4. Последовательное и параллельное соединение сопротивлений

При последовательном соединении участков цепи комплексное эквивалентное сопротивление равно сумме комплексных сопротивлений отдельных участков [5, 6]:

С	n
	Z = ∑ Z k .	(2.40)
	k=1
	k=1

При параллельном соединении ветвей комплексная эквивалент-

ная провод мость равна сумме комплексных проводимостей ветвей
ний	n
	Y = ∑Y k .	(2.41)
	k=1

	б
В частном случае двух параллельно соединённых сопротивле-
Z1	Z 2 экв валентное комплексное сопротивление
	Z =	Z1 Z 2	.	(2.42)
		Z1 + Z 2
Комплексные токи, протекающие в каждой из двух параллельных
ветвей,	могут быть рассчитаны через комплексный ток I			в неразветв-

лённой части цепи и комплексные сопротивления ветвей по формулам

		Z 2				Z1
			Д

I1	= I	Z + Z	; I2	= I	Z	+ Z	.	(2.43)
А1 2 1 2

2.1.5. Законы Кирхгофа для цепей синусоидального тока

Для записи уравнений на основании законов Кирхгофа необходимо выбрать положительные направления для всех токов и обозначить их на схеме [5, 6].

Первый закон Кирхгофа в комплексной форме в применении к
узлу электрической цепи переменного синусоидального тока имеет
вид [5, 6]:	И
n
∑ Ik = 0 .	(2.44)
k=1

При записи этого уравнения токи, направленные к узлу, следует записать со знаком плюс, а направленные от узла – со знаком минус (или наоборот).

Второй закон Кирхгофа применяется к замкнутому контуру цепи переменного синусоидального тока и имеет вид [5, 6]:

∑ Ik Z k

= ∑E p ,

(2.45)

Со

k=1

p=1

где ∑ Ep

– алгебраическая сумма комплексных ЭДС источников на-

p =1

пряжен я.

знаком плюс записываются те из них, положительные

направлен я которых совпадают с выбранным направлением обхода

минус

контура; ЭДС,

меющ е направления, противоположные обходу кон-

тура, зап сываются со знаком минус;

∑ I k Z k

– падения напряжений

Z k

k =1

на комплексных сопротивлениях

отдельных участков. Со знаком

обхода

берутся те, для которых направление тока противоположно на-

правлен ю

контура.

При составлен

уравнений по второму закону Кирхгофа следу-

ет выб рать незав с мые контуры, не содержащие источников тока.

2.1.6. Комплексная мощность. Баланс мощностей

Комплексная мощность в цепи синусоидального тока определя-

ется по формуле [5, 6]:

= U

(2.46)

I = UI cosϕ + jUI sin ϕ = P + jQ = Se jϕ ,

где S

–

полная

мощность,

S = UI ;

–

активная

мощность,

P = Re[S]= UI cosϕ; Q – реактивная мощность, Q = Im[S]

= UI sin ϕ;

ϕ – угол сдвига фазы между током

I – сопряжённый комплекс тока;

и напряжением.

Баланс мощностей имеет вид [5, 6]:

[I 2 R

+ jI 2

− X

)].

(2.47)

∑

I p =

∑

p=1

k =1

Здесь

∑ Ep I p

– алгебраическая мощность всех источников ЭДС;

p=1

положительны те из слагаемых, для которых направление действия ЭДС Ep и соответствующего тока I p через ЭДС совпадают, в про-

тивном случае слагаемое отрицательно;

= P – алгебраическая

∑ I 2 R

k=1

сумма мощностей на активных сопротивлениях (здесь должны быть

учтены как внешние сопротивления, так и сопротивления самих ис-

точников энергии);

= Q

– алгебраическая сумма

∑ Ik2 X Lk

− ∑ Ik2 XCk

k=1

мощностей на реактивных сопротивлениях.

2.2. Пр мер расчёта однофазной цепи синусоидального тока

При расчёте цепей переменного тока посредством комплексных

остаются справедливыми все методы расчёта, применяемые для

цепей постоянного тока. При этом во всех уравнениях ЭДС, напряже-

ния, токи, сопрот влен я и проводимости должны быть записаны в

комплексной форме.

чисел

Рассмотр м пр мер расчёта разветвлённой однофазной цепи

синусо дального тока с одним источником переменной ЭДС,

имею-

щей следующие электрические параметры:

•

мгновенное значение напряжения на участке цепи

uR2(t) =

100sin(200t – 60°).

• величины резистивных сопротивлений R2 = R3 = 5 Ом;

• величина индуктивности L1 = 10 мГн;

•

величина ёмкости C3

= 500 мкФ.

Схема замещения разветвлённой однофазной электрической це-

пи представлена на рис. 2.6, а.

uL1

uR3

U mL1

UmR3

jXL1

Im2

R3 -jXС3

Im3

uR2

uC3

UmC3

С3

ИU

Еm

Рис. 2.6. Разветвлённая цепь синусоидального тока:

а) схема замещения; б) расчётная схема

Для вышеприведенной однофазной цепи необходимо:

1. Найти мгновенные и действующие значения токов в ветвях,

применяя:
-	законы Кирхгофа;
-	метод контурных токов;
С
-	метод эквивалентных преобразований.
2. Найти мгновенные и действующие значения ЭДС и напряже-
ний на всех элементах.
3.	остав ть баланс мощностей цепи.

4. Постро ть векторную диаграмму токов и напряжений.

ниямиМетод ка расчёта:

На р с. 2.6, зо ражена расчётная схема электрической цепи, для которой сходные данные о параметрах всех элементов представлены в комплексной форме. Вы ерем положительные направления неизвестных токов в ветвях (рис. 2.6, а) и совпадающие с направлетоков полож тельные направления напряжений на пассивных элементах, полож тельные направления соответствующих комплекс-

ных значен й тока напряжения такие же (рис. 2.6, б).
А
Представим напряжение uR2 в комплексной форме (2.4):
б− j60°		.
UmR2 =100e
Определим комплексные значения индуктивного и ёмкостного
сопротивлений (2.20), (2.21):
X L1 = ωL1 = 200 10 10	−3		= 2 Ом;

jX L1 = j2 = 2e j90° Ом;

XC3 = 1 (ωC3 ) = 1 (200 500 10	−6 ) = 10 Ом;
	И
Д− j90°
− jXC = − j10 =10e	Ом.
3

Определение неизвестных токов, напряжений и ЭДС может проводиться любым методом расчёта линейных электрических цепей.

Рассмотрим расчёт данной цепи, применяя законы Кирхгофа и закон Ома.

При выбранных положительных направлениях токов и напряжений составим полную систему уравнений для анализа цепи. По первому закону Кирхгофа (2.44) для узла а:

Im1 − Im2 − Im3 = 0.

По второму закону Кирхгофа (2.45) для двух независимых контуров уравнения имеют вид

UmL1 +UmR2 = Em ;

UmR3 +UmC3 −UmR2 = 0

или

+ R I

= E

;

(R − jX

− R I

= 0.

напряжения

стема уравнен й,

составленных по законам Кирхгофа, с учё-

том заданного

−U

− I

= 0;

jX L1Im1

+UmR

Em ;

− jX

−U

mR2

= 0.

После подстановки числовых значений система примет вид

Im1 − Im3

= 20e− j60°

− j17,32;

j2Im1

− Em = −100e− j60°

= −50 + j86,5;

(5 − j10)Im3 = 100e− j60° = 50 − j86,5.

Значение тока I

определяем из третьего уравнения системы

Im3 =

100e− j60°

= 8,94e

3,43°

= (8,92 + j0,53) А,

11,18e− j63,43°

а значение тока Im1 – из первого уравнения системы

Im1 =10 − j17,32 + Im3

=18,92 − j16,79 = 25,30e− j41,59° А.

Комплексную амплитуду ЭДС находим из второго уравнения

системы

Em = j2Im1 + 50 − j86,5 = j37,84 + 33,58И+ 50 − j86,5 =

= 83,58 − j48,66 = 96,71e− j30,21°В.

Величину тока Im2 вычислим, используя закон Ома

Im2

UmR2

= 100e− j60°

= 20e− j60° А.

Рассмотрим применение метода контурных токов для цепи, изображённой на рис. 2.6. Применение этого метода позволяет сократить количество одновременно решаемых уравнений с трёх до двух.

Обозначим контурный ток контуре с источником ЭДС Im11 , в контуре

без источника ЭДС –

Im22 , тогда система уравнений будет иметь вид

(jX

+ R

− R I

= E

;

+ (R2 +R3 − jXC3 )Im22 = 0.

− R2 Im11

Комплексные значения токов в ветвях

ходимо

− I

;

= I

;

= I

m11

m22

учётом заданного значения uR2

Im2 = UmR2 R2 ,

контурный ток I

нео

представить в виде

m22

= I

− I

= I

−U

mR2

R .

m22

m11

запишется в виде

Тогда исходная система уравнений при R2

= R3

(jX L1

+ R2 )Im11

− R2 (Im11

−UmR2 R2 )

= Em ;

− R2 Im11 + (2R2 − jX C3 ) (Im11 −U mR2 R2 )= 0.

+ R I

− R I

mR2

= E

;

m11

− R2 Im11 + 2R2 Im11 − jXC3Im11 − 2UmR2 + (jXC3 R2 )UmR2 = 0.

Получим систему уравнений относительно неизвестных значе-

ний Im11 и Em .

m11

− E

=Д−U ;

mR2

(R2 − jXC3 )Im11 =

(2 − jXC3

R2 )UmR2 .

После подстановки числовых значений система примет вид

= −100e

− j60°

= −50 + j86,5;

j2I

m11

− E

(5 − j10)Im11 = (2 − j2) 100e− j

60°.

Из второго уравнения системы найдём значение тока Im11.

Im11 =

2,83e− j45° 100e− j60°

= 25,31e− j41,57° = (18,94 − j16,79) А.

11,18e− j63,43°

Комплексная амплитуда ЭДС

Em = j2(18,94 − j16,79)+ 50 − j86,5 = 83,58 − j48,62 = 96,69e− j30,19° В.

Значение контурного тока Im22

= I

−U

mR2

=18,94 − j16,79 −10 + j17,3 = (8,94 + j0,51) А.

m22

m11

Комплексные амплитуды токов в ветвях

Im1

= Im11, Im1 = Im11 = 25,31e− j41,57° А;

Im2 = Im11 − Im22 =18,94 − j16,79 − 8,94 − j0,51 =10 − j17,3 = 20e− j60 А;

= Im22

= 8,94 + j0,51 = 8,95e

j3,26

А.

Im3

Полученные комплексные значения токов и ЭДС практически

совпадают с найденными ранее величинами путём непосредственного

я первого

второго законов Кирхгофа.

применен

Для расчёта цепей синусоидального тока также применяют

метод экв валентных прео разований.

Проведём эквивалентное преобразование схемы (рис.2.7).

Im1

Еm

Im2

Аm3

Z Э

Z 2

Z 3

Дб в

Рис. 2.7. Метод эквивалентных преобразований

Найдём комплексные сопротивления ветвей (рис. 2.7, а):

первой:

= jX L1

= X L1e

j90

= j2 =

Иj90°

Ом;

второй:

Z 2 = R2 = 5 Ом;

−10

третьей: Z

= R

− jX

= 5 − j10 =

+102 e

jarctg

= 11,18e− j63,43° Ом.

Определим эквивалентное комплексное сопротивление параллельного соединения второй и третьей ветви с токами I2 и I3 (рис. 2.7, б):

Z 23 =

11,18e− j63,43°

55,9e− j63,43°

= 3,95e

−

j18,43

+ 5

− j10

Z 2 + Z 3

14,14e− j45

С
= 3,95cos(−	18,43°)+ j3,95sin(−18,43°) = (3,75 − j1,25) Ом.
Входное комплексное сопротивление цепи (рис. 2.7, в):
Z Э = Z1 + Z 23	= j2 + 3,75 − j1,25 = 3,75 + j0,75 = 3,82e j11,31° Ом.
и
Поскольку	звестно напряжение на резистивном элементе U mR2 ,
сначала определяем ток Im2		по закону Ома для данного элемента
	UmR2			100e− j60°		− j60°
б					= 20e		А.
	Im2 = R2		=	5	= 20e		А.

Напряжен е между узлами цепи a и b по закону Ома (см. рис. 2.7) является напряжен ем каждой из параллельных ветвей

U m ab = Im1 Z 23

= Im Z 2

= Im Z 3 = U mR2 .

Найдём комплексные значения токов Im1 ,

Im3 :

Im1 =

U mR2

100e− j60°

= 25,32e

− j41,57°

А;

Z 23

3,95e− j18,43°

Im3

= U mR2

100e− j60°

= 8,94e j3,43°

А.

11,18− j63,43°

Z 3

ЭДС источника

Em = Im1 Z Э = 25,32e

− j41,57°

j11,31°

− j30,26°

Д3,82e = 96,72e В.

Полученные комплексные значения токов и Э С практически совпадают с найденными ранее величинами.

Комплексные амплитуды напряжений определяем по закону
Ома для резистивного (2.14), индуктивного (2.23)Ии ёмкостного (2.34)
элементов:
U	mR3	= R I	= 5 8,94e j3,43° = 44,7e j3,43° В;
	mR3	3 m3

UmL1 = jX L1Im1 = 2e j90° 25,30e− j41,59° = 50,6e j48,41° В;

UmC3 = − jXC3Im3 = 10e− j90° 8,94e j3,43° = 89,e− j86,57° В.

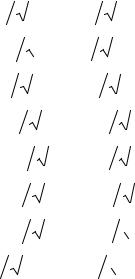
Мгновенные значения токов и напряжений:

i (t) = 25,3sin(200t − 41,59 )А;

20sin(200t − 60 )А;

(t) =

= 8,94sin(200t + 3,43 )А;

i3 (t)

uL1(t) = 50,6sin(200t + 48,41 )В;

uR3 (t) = 44,7 sin(200t + 3,43 )В;

действующие

3 (t)

= 89,4sin(200t − 86,57 )В;

e(t) = 96,71sin(200t − 30,21 )В.

Рассч таем

значения токов и напряжений:

I1 = Im1

= 25,3

= 17,89А;

I2 = Im2

= 20

= 14,14 А;

= Im3

= 8,94

= 6,32

;

U = U 2 = 50,6 2 = 35,78В;

mL1

UR2 = UmR2

= 100

= 70,71В;

UR3 = UmR3

ЭДС

= 44,7

= 31,61В;

UC3 = UmC3

= 89,4

2 = 63,22 В;

E = Em

= 96,71

2 = 68,38 В.

Проверим решение,

составив баланс мощностей (2.47). Для эт о-

го найдём мощность источника

(2.46) и представим её в алгеб-

раической форме записи комплексного числа

+ jQ

= 68,38e− j30,21° 17,89e j41,59° = 1223,3e j11,38° =

ИСТ

= 1223,3cos11,38° + j1223,3sin11,38° = (1199,3 + j241,4) ВА.

Активная мощность источника PИСТ = 1199,3 Вт.

Реактивная мощность источника QИСТ = 241,4 вар.

Активная и реактивная мощности приёмников:

= I 2 R

+ I 2 R =14,142 5 + 6,322 5 = 1199,4 Вт;

ПР

QПР = I12 X L1 − I32 X C3

=17,892 2 − 6,322 10 = 240,7 вар.

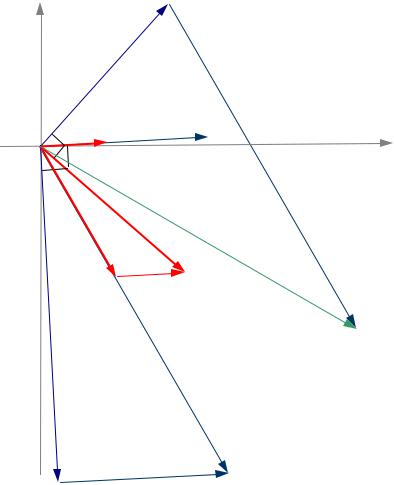
Учитывая погрешность округления при расчётах, можно считать, что баланс мощностей выполняется.

Построим векторную диаграмму токов и напряжений на

комплексной плоскости (рис. 2.8). Сначала выберем масштаб: 1 см

соответствует 5 А тока и 10 В напряжения. От начала координат от-

кладываем векторы, длина которых пропорциональна амплитудному

значению тока, напряжения или ЭДС, а угол поворота относительно

действительной оси +1 совпадает с начальной фазой.

UmL1

UmR3

Im3

Im1

Im2

UmR2

Im3

UmС3

mR2

UmR3

Рис. 2.8. Векторная диаграмма токов и напряжений

в цепи синусоидального тока

Анализ диаграммы позволяет сделать следующие выводы:

напряжение на индуктивном элементе UmL1 опережает ток

Im1 на 90°;

напряжения на резисторах UmR2 и

UmR3 совпадают по фазе

соответственно с токами Im2 ,

Im3 ;

-напряжение на ёмкостном элементе UmC3 отстает по фазе от тока Im3 на 90°;

-вектор Im1 определяется геометрической суммой векторов

Im2

и Im3 , следовательно, выполняется первый закон Кирхгофа;

выполнение

второго

закона

Кирхгофа

можно

проверить,

сложив векторы UmL1

и UmR2 , их сумма должна дать вектор Em .

2.3. Исходные данные для расчёта

Для расчёта на р с. 2.9 приведены различные схемы замещения

Сэлектр ческ х цепей с

нусоидального тока.

uC1

Схема 1

Схема 2

uL1

С1

uR3

uL2

С2

uC2

uR1

uC1

Схема 3

uR1

Схема 4

i uC

С1

uL2

uR3

С2

uC2

С3

uC3

uL3

uC1

Схема 5

uL1

Схема 6

uR3

С1

uR3

uR2

uL3

С2

uC2

uL3

Рис. 2.9. Схемы замещения электрических цепей синусоидального тока

	Вариант исходных данных для расчёта состоит из номера схемы
и буквы набора параметров цепи (например, «2б»). Параметры элемен-
тов цепей и заданная электрическая величина участка цепи приведе-
ны в табл. 2.1. Согласно примеру для своего варианта исходных данных
необходимо:
	1. Найти мгновенные и действующие значения неизвестных то-
ков в ветвях, применяя один из перечисленных ниже методов
	- метод непосредственного применения законов Кирхгофа;
	-	метод контурных токов;
	-	метод экв валентных преобразований.
	2. Найти мгновенные и действующие значения ЭДС и напряже-
С
	на всех элементах.
	3.	остав ть аланс мощностей.
	4. Постро ть векторную диаграмму токов и напряжений.
ний			Таблица 2.1
ний
		Параметры электрических цепей синусоидального тока
Вар.		Параметры элементов ветвей	Заданная величина
		б
		Схема 1
а	R1 = R3 = 6 Ом; L2 = 20 мГн; С1 = 400 мкФ		uR3 = 11,5sin(500t + 43°) В
б	R1 = R3 = 5 Ом; L2 = 60 мГн; С1 = 1000 мкФ		e = 26sin100t В
в	R1 = R3 = 2 Ом; L2 = 30 мГн; С1 = 1000 мкФ		i1 = 1,25sin(200t + 32°) А
г	R1	= R3 = 4 Ом; L2 = 50 мГн; С1 = 2500 мкФ	uR1 = 20,5sin(100t – 45°) В
д		А
д	R1 = R3 = 4 Ом; L2 = 30 мГн; С1 = 500 мкФ		uС1 = 25sin(200t + 13°) В
е	R1 = R3 = 6 Ом; L2 = 20 мГн; С1 = 625 мкФ		uR3 = 37,5sin(400t – 78°) В
ж	R1 = R3 = 1 Ом; L2 = 10 мГн; С1 = 2500 мкФ		i2 = 5sin(1000t + 26°) А
з	R1 = R3 = 10 Ом; L2 = 10 мГн; С1 = 200 мкФ		i3 = 0,75sin(500t – 61°) А
и	R1	= R3 = 10 Ом; L2 = 40 мГн; С1 = 500 мкФ	uL2 = 7,5sin(200t + 113°) В
к		Д
к	R1 = R3 = 3 Ом; L2 = 10 мГн; С1 = 400 мкФ		e = 36sin500t В
		Схема 2
а	R1 = R3 = 7 Ом; L1 = 10 мГн; С2 = 312,5 мкФ		i2 = 10,8sin(400t + 46°) А
б	R1 = R3 = 4 Ом; L1 = 4 мГн; С2 = 1000 мкФ		i3 = 6,5sin(500t + 48°) А
в	R1 = R3 = 6 Ом; L1 = 100 мГн; С2 = 2500 мкФ		uL1 = 37,5sin(100t – 10°) В
г	R1 = R3 = 5 Ом; L1 = 30 мГн; С2 = 500 мкФ		И
	R1 = R3 = 5 Ом; L1 = 30 мГн; С2 = 500 мкФ		uС2 = 20,5sin(200t – 13°) В
д	R1 = R3 = 4 Ом; L1 = 12,5 мГн; С2 = 625 мкФ		uR1 = 40sin(400t + 25°) В
е	R1 = R3 = 8 Ом; L1 = 20 мГн; С2 = 200 мкФ		e = 40sin500t В
ж	R1 = R3 = 9 Ом; L1 = 30 мГн; С2 = 500 мкФ		i1 = 15,25sin(200t + 36°) А
з	R1 = R3 = 1 Ом; L1 = 10 мГн; С2 = 1250 мкФ		uR3 = 2,5sin(400t – 48°) В
и	R1 = R3 = 5 Ом; L1 = 30 мГн; С2 = 500 мкФ		uС2 = 32sin(200t – 13°) В
к	R1 = R3 = 6 Ом; L1 = 10 мГн; С2 = 400 мкФ		uL1 = 20,5sin(500t – 10°) В
		49

Схема 3

R3 = 8 Ом; L2 = 30 мГн; С1 = C3 = 500 мкФ

uС1 = 20,5sin(200t +34°) В

R3 = 7 Ом; L2 = 10 мГн; С1 = C3 = 312,5 мкФ

i2 = 10,8sin(400t – 56°) А

R3 = 6 Ом; L2 = 90 мГн; С1 = C3 = 2500 мкФ

uL2 = 41,5sin(100t + 15°) В

R3 = 5 Ом; L2 = 30 мГн; С1 = C3 = 500 мкФ

uС3 = 27,5sin(200t – 65°) В

R3 = 4 Ом; L2 = 12,5

мГн; С1 = C3 = 625 мкФ

uR3 = 24sin(400t + 63°) В

R3 = 3 Ом; L2 = 4 мГн; С1 = C3 = 1000 мкФ

i3 = 8,5sin(500t – 20°) А

R3 = 2 Ом; L2 = 20 мГн; С1 = C3 = 2500 мкФ

e = 14sin100t В

R3 = 1 Ом; L2 = 10 мГн; С1 = C3 = 625 мкФ

i1 = 5,25sin(400t – 99°) А

R3 = 9 Ом; L2 = 40 мГн; С1 = C3 = 500 мкФ

uС1 = 30,2sin(200t + 15°) В

R3 = 10 Ом; L2 = 12,5 мГн; С1 = C3 = 156,25 мкФ

uR3 = 24sin(800t – 42°) В

Схема 4

uR1= 44sin(400t+23°) В

R1 = R3 = 10 Ом; L3 = 10 мГн; С2 =312,5 мкФ

R1 = R3 = 9 Ом; L3 =

мГн; С2 = 500 мкФ

uС2 = 25sin(200t-13°) В

R1 = R3 = 8 Ом; L3

мГн; С2 = 100 мкФ

i3 = 2,75sin(500t-61°) А

R1 = R3 = 7 Ом; L3

мГн; С2 = 625 мкФ

uR3 = 30,5sin(400t+108°) В

R1 = R3 = 5 Ом; L3 =

мГн; С2 = 1000 мкФ

e = 46sin100t В

R1 = R3 = 4 Ом; L3 =

мГн; С2 = 312,5 мкФ

i2 = 16,8sin(400t-66°) А

R1 = R3 = 8 Ом; L3 =

мГн; С2 = 500 мкФ

i1 = 15,5sin(200t+30°) А

R1 = R3 = 6 Ом; L3 =

мГн; С2 = 1000 мкФ

uL3 = 60,5sin(100t-15°) В

R1 = R3 = 2 Ом; L3 =

мГн; С2 = 2500 мкФ

e = 24sin100t В

R1 = R3 = 4 Ом; L3 = 12,5 мГн; С2 = 625 мкФ

uR1 = 40sin(400t-25°) В

Схема 5

R2 = R3 = 6 Ом; L3 =

мГн; С1 = 200 мкФ

e = 45sin500t В

R2 = R3 = 5 Ом; L3

мГн; С1 = 500 мкФ

uС1 = 60sin(200t – 113°) В

R2 = R3 = 4 Ом; L3

4 мГн; С1 = 1000 мкФ

i3 = 6,5sin(500t + 88°) А

R2 = R3 = 1 Ом; L3

= 10 мГн; С1 = 1250 мкФ

uR3 = 4,5sin(400t + 43°) В

R2 = R3 = 2 Ом; L3 =

мГн; С1 = 1000 мкФ

i1 = 2,25sin(200t – 32°) А

R2 = R3 = 5 Ом; L3 =

мГн; С1 = 1000 мкФ

uL3 = 40,5sin(100t – 55°) В

R2 = R3 = 6 Ом; L3 =

мГн; С1 = 400 мкФ

uR3 = 12,5sin(500t + 14°) В

R2 = R3 = 4 Ом; L3 =

мГн; С1 = 2500 мкФ

uR2 = 24,5sin(100t – 45°) В

R2 = R3 = 1 Ом; L3 =

мГн; С1 = 2500 мкФ

i2 = 4sin(1000t – 26°) А

R2 = R3 = 5 Ом; L3 =

мГн; С1 = 500 мкФ

uС1 = 35sin(200t + 13°) В

Схема 6

R3 = 6 Ом; L1 = L3 = 100 мГн; С2 = 2500 мкФ

uL1 = 27,5sin(100t + 10°) В

R3 = 8 Ом; L1 = L3 = 20 мГн; С2 = 200 мкФ

e = 30sin(500t + 45°)В

R3 = 7 Ом; L1 = L3 = 10 мГн; С2 = 312,5 мкФ

i2 = 10,5sin(400t – 56°) А

R3 = 4 Ом; L1 = L3 = 4 мГн; С2 = 1000 мкФ

i3 = 6,5sin(500t – 58°) А

R3 = 6 Ом; L1 = L3 = 20 мГн; С2 = 625 мкФ

uR3 = 30,5sin(400t + 70°) В

R3 = 4 Ом; L1 = L3 = 30 мГн; С2 = 500 мкФ

uС2 = 25sin(200t – 103°) В

R3 = 6 Ом; L1 = L3 = 90 мГн; С2 = 2500 мкФ

uL3 = 21,5sin(100t + 15°) В

R3 = 1 Ом; L1 = L3 = 10 мГн; С2 = 625 мкФ

i1 = 5,5sin(400t – 100°) А

R3 = 2 Ом; L1 = L3 = 20 мГн; С2 = 2500 мкФ

e = 24sin100t В

R3 = 4 Ом; L1 = L3 = 12,5 мГн; С2 = 625 мкФ

uR3 = 8,2sin(400t – 63°) В

	Контрольные вопросы и задания
1.	Какие параметры определяют синусоидальные функции вре-
мени? Какие параметры синусоидальной величины можно предста-
вить с помощью вектора?
С
2.	Какие формы представления комплексных чисел используют
для отображения синусоидальных функций времени? Для каких ма-
тематических операций используют алгебраическую и показательную
форму комплексных ч сел?
3.	Как соотносятся по фазе ток и напряжение резистивного (ин-
тивного
дуктивного, ёмкостного) элемента?
4.	Как зав сят от частоты сопротивления резистивного (индук-
	, ёмкостного) элемента? Чему равно индуктивное (ёмкостное)
сопрот влен е при постоянном токе?
5.	Что называют комплексным сопротивлением пассивного
двухполюсн ка? Зап ш те формулу для полного сопротивления пас-
сивного двухполюсн ка.
6.	Что называют комплексной проводимостью пассивного
	А
двухполюсника? Запишите формулу для полной проводимости пас-
сивного двухполюсникаб.
7.	В каких пределах может находиться значение угла сдвига
фаз между током и напряжением в пассивной электрической цепи? От
какого вектора отсчитывается угол сдвига фаз?
8.		Д
	Сформулируйте законы Кирхгофа для цепи синусоидального
тока.
9.	Дайте определения активной, реактивной и полной мощностей.
10.	Сформулируйте условие баланса мощностей в электрической
цепи синусоидального тока.			И

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20213.01 Mб22093.pdf
#
07.01.20213.01 Mб72094.pdf
#
07.01.20213.02 Mб12096.pdf
#
07.01.20213.02 Mб52097.pdf
#
07.01.20213.02 Mб22098.pdf
#
07.01.20213.05 Mб182099.pdf
#
07.01.2021204.41 Кб021.pdf
#
07.01.2021348.98 Кб3210.pdf
#
07.01.20213.05 Mб52100.pdf
#
07.01.20213.05 Mб422101.pdf
#
07.01.20213.07 Mб422102.pdf