baldin_kv_red_matematika_dlia_gumanitariev

число (2.22), называют n-мерным векторным пространством и обозначают Rn (в случае n = 1 оно совпадает с множеством действительных чисел R).

В случае n = 2 и n = имеем соответственно двумерное (R2) и трехмерное (R ) векторные пространства, а двумерные и трехмерные вектора имеют геометрическую интерпретацию: они изображаются направленными отрезками на плоскости и в пространстве [ , 12, 1 ].

Пусть в Rn заданы вектора

,

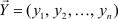
Приведем свойства линейных действий векторами [ , 12]: 1) 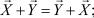2) ) 4)

5)

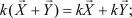
6)

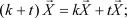
7)

8)

9)

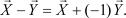
Длина (норма) вектора в пространстве Rn находится по формуле

(2.2 )

Например, задан вектор = (5, , –2). Используя (2.2 ) найдем, что его длина равна

Введем понятие скалярного произведения в действительном пространстве Rn.

81

Скалярным произведением двух векторов

= (x1, х2, …, хn) и = (у1, у2, …, уn)

в Rn (хi[Rn, уi[Rn, 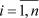) называется число, получаемое по формулам [ , 12, 1 ]:

(2.24)

(2.25)

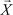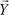где есть угол между n-мерными векторами и (в случае n = 2 и n = будет углом между направленными отрезками на плоскости и в пространстве, а при n > векторы и являются математическими абстракциями).

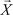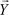Из формулы (2.25) следует, что угол между n-мерными векторами и равен

(2.26)

Если угол между векторами и равен , то скалярное произведение этих векторов равно нулю, т. е.

(2.27)

Пример 2.7.

Например, заданы векторы

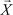= (2, , 7) и 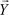= (1, 6, 5) в -мерном пространстве R . Найти угол между ними.

По формуле (2.26) получим

82

Скалярное произведение в пространстве Rn обладает следующими свойствами [ , 12]:

1) (при этом равенство нулю будет только в том случае, если );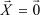

2))

Здесь 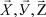— векторы в Rn, а k и t — действительные числа.

Пространство Rn, в котором введено понятие скалярного произведения по формуле (2.24), называется евклидовым n- мерным пространством [ , 12].

Задачидлясамостоятельногорешения

1. Найти произведения матриц

1.1.

1.2.

1. .

2. Вычислить определители:

2.1. 2.2.

8

2. .

. Найти матрицы, обратные данным:

4. .

5. Решить СЛАУ методами Гаусса и Крамера:

5.1. 5.2.

5. .

6. Найти собственные числа и собственные векторы матриц:

6.1. 6.2. 6. .

84

6.4.

7. Дано: 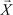= (1, –5, 6, 7, 10); 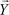= (–2, 7, 8, 11, –6).

Найти угол между векторам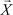и и 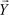. 8. Даны два ортогональных вектора

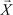= ( , х2, 7) и = (1, 6, 8).

Найти координату х2.

вопросыдлясамопроверки

1.Что называется матрицей? Типы матриц.

2.Правило и свойства сложения матриц.

. Правило и основные свойства перемножения двух матриц.

4.Как найти матрицу, обратную заданной? Любая ли матрица имеет обратную?

5.Что называется определителем?

6.Что такое ранг матрицы?

7.Как определить, совместна ли заданная СЛАУ?

8.В каких случаях однородные СЛАУ имеют ненулевые решения?

9.В чем суть итерационных методов решения СЛАУ?

10.В чем состоит метод Гаусса решения СЛАУ?

11.В чем состоит метод Крамера решения СЛАУ?

12.Какие числа называются собственными значениями матрицы?

1 . Что такое след матрицы?

14.Какое уравнение называется характеристическим уравнением матрицы?

15.Дать определение n-мерного векторного пространства.

16.Что называется нормой вектора?

17.Как найти угол между двумя векторами в n-мерном векторном пространстве?

18.Какое n-мерное пространство называется евклидовым?

85

3.ФункциииПределы

3.1.некоторыесведенияофункциях

Влюбой области науки мы встречаемся с различными величинами. Под величиной понимают все то, что может быть измерено и (или) вычислено и выражено числом или числами [2].

Вестественных, технических и гуманитарных науках имеют дело с различными величинами, например, скоростью, силой, температурой, себестоимостью, валовым внутренним продуктом какой-либо страны, количеством преступлений в каком-то регионе и др.

Ав математике конкретные величины не участвуют, т. е. рассматривают величины вообще, не принимая во вниманиe их физический смысл.

Все величины можно разделить на переменные и постоянные.

Переменной называется такая величина, которая принимает различные числовые значения. Величина, которая не меняет свое числовое значение, называется постоянной.

Все процессы характеризуются взаимоизменяемостью нескольких переменных величин, а это приводит к важнейшему понятию математики функциональной зависимости.[2, 22]

Часто одни и те же величины могут в одних случаях быть переменными, а в других постоянными.

Например, в формуле F = ma величины m (масса) и a (ускорение) могут быть как постоянными, так и переменными.

Но существуют и фундаментальные постоянные, которые сохраняют свое значение, по крайней мере, в нашей Mетага-

лактике.

Например, в законе всемирного тяготения 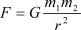ве-

Установление и описание связей между величинами одна из основных задач математического анализа, который включа-

86

ет в себя ряд дисциплин: теорию пределов, дифференциальное и интегральное исчисления, теорию рядов и др. [2]. Некоторые сведения из этих дисциплин мы рассмотрим в главах –7.

Теперь приведем определение функции одного независимого аргумента.

Переменная величина y называется функцией переменной величины x на множестве

определенияD,есликаждому значению x [D по како- му-то закону поставлено в

соответствие одно (несколько, бесконечно много) значение (значений) y [2, 20].

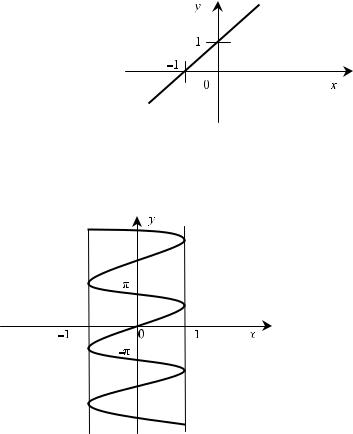
В первом случае функцияназываетсяоднознач-

ной, например, y = x + 1 (рис. .1).

Авовторомслучае—многозначной,например,y=Arcsin x

(рис. .2).

Рис. 3.2

Величину x из области D можно брать произвольно, поэтому она называется аргументом или независимой переменной. А

87

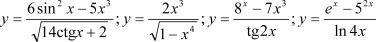
величина y будет зависеть от выбранной величины x, поэтому ее называют зависимой переменной или функцией.

Область D может быть любой, но, как правило, используются области двух видов:

множество целых неотрицательных чисел или какие-то части этого множества;

один или несколько интервалов (конечных или бесконечных) числовой оси.

В первом случае имеем функцию целочисленного аргумента, а во втором — непрерывного.

Тот факт, что величина y есть функция аргумента x, обычно записывают так: y = f(x).

Множество всех значений функции y обозначим через E. Функцию можно задать с помощью таблицы, в виде гра-

фика (преимуществом этого способа является его наглядность) или аналитически (формулой). Последний способ является самым распространенным.

Все функции можно разделить на два класса: элементарные и неэлементарные.

К элементарным функциям относятся основные элементарные функции:

y = xn (n [ R), y = ax (a > 0, a 1),

y = loga x (a > 0, a 1), y = sin x, y = cos x, y = tg x, y = ctg x, y = sec x, y = cosec x,

y = arcsin x, y = arccos x, y = arctg x, y = arcctg x

и функции, полученные из основных элементарных функций при помощи конечного числа арифметических действий и конечного числа операций взятия функции от функции и заданные одной формулой [22].

Например,

и т. д.

Все функции, не подходящие под данное определение, элементарными функциями не являются.

88

Например, функция

-1 при x < 0; 0 при x = 0;

1 при x > 0

не является элементарной функцией, так как задана тремя формулами [6, 22].

А функция f(n) = 1 · 2 · · … n = n! не будет элементарной, так как количество операций умножения, которое нужно совершить для получения f(n), не будет являться конечным.

3.2.Пределпоследовательности.Пределфункции. вычислениепределов.

Прежде чем перейти к определению предела напомним, что в математике используются три вида бесконечностей +`, -`, `. Бесконечность не является числом, она показывает, как меняется переменная величина, которая конечна в любой момент времени.

Теперь определим понятие последовательности и ее предела.

Последовательностью называется множество чисел, которое перенумеровано с помощью целых чисел и расположено в порядке возрастания номеров [2].

Если задана последовательность y1, y2, y , …, то тем самым любому целому неотрицательному значению n поставлено в соответствие значение yn = f(n).

Например, члены геометрической прогрессии

являются последовательными значениями функции , где n [ Z+, Z+ — целые положительные числа.

Может случиться так, что с увеличением n значения yn = = f(n) будет неограниченно приближаться к какому-то числу a. В этом случае говорят, что число a является пределом функции

89

Число a является пределом последовательности y1, y2, …, yn, …, если для ; > 0 можно найти такое N > 0, что для всех f(n) с номерами n > N справедливо неравенство [2, 22]

Таким образом, мы доказали, что для любого наперед за-

будет выполняться ( .1.), а это означает, что 1 есть предел исходной последовательности.

Теперь рассмотрим функцию y = f(x) непрерывного аргумента x (рис. . ) и предположим, что x неограниченно приближается к числу x0 (x → x0). При этом может оказаться, что соответствующее значение f(x) неограниченно приближается к некоторому числу b. В этом случае говорят, что число b есть предел функции f(x) при (x → x0).

Рис. 3.3

90