baldin_kv_red_matematika_dlia_gumanitariev

Пример 5.16.

Применим подстановку и получаем:

[Воспользуемся формулой 16 из таблицы интегралов.]

С помощью указанной подстановки хорошо “берутся” ин-

щности она не всегда является оптимальной.

5.2.Определенныйинтеграл

К понятию определенного интеграла можно прийти рассматривая различные задачи, например нахождение площади плоской фигуры, вычисление работы переменной силы, определение пути по заданной переменной скорости.

Найдем площадь криволинейной трапеции, т. е. фигуры, которая ограничена осью 0х, графиком непрерывной функции y = f(x) и двумя прямыми x = a и x = b (рис. 5.2). Пока будем считать, что криволинейная трапеция расположена над осью

0х, т. е. f (x) > 0.

Разделим отрезок [a, b] на n частичных интервалов: [x0, x1],

[x1, x2], …, [xn-1, xn].

В точках деления отрезка [a,b] проведем прямые, параллельные оси 0y, и разобьем криволинейную трапецию aABb

161

Рис. 5.2

на n частичных трапеций. В каждом из частичных интервалов возьмем по произвольной точке М1, М2,…, Мn (некоторые из этих точек могут совпадать с точками деления отрезка [a, b]).

Через точки М1, М2,…, Мn проведем прямые, параллельные оси 0y до пересечения с функцией y = f (x). Отрезки этих прямых f (M1), f (M2), …, f (Mn) есть ординаты графика функции y = f (x). Взяв частичные интервалы за основания, построим на них n прямоугольников с высотами, равными f (M1), f (M2), …, f (Mn). В результате мы получим ступенчатую фигуру, состоящую из n прямоугольников. Так как площадь любого из прямоугольников будет равна f (Mi)(xi – xi - 1), 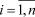, то площадь ступенчатой фигуры можно найти по формуле

(5.5)

162

При неограниченном увеличении количество частичных интервалов (n → `) и при стремлении длины наибольшего из них к нулю ступенчатая фигура будет неограниченно приближаться к криволинейной трапеции aABb, т. е. получим

(5.6)

Зная площадь криволинейной трапеции, мы можем находить площади любых плоских фигур (этот вопрос мы подробнее рассмотрим ниже). К выражению вида (5.6) приводят и другие задачи (нахождение работы переменной силы, вычисление пути по заданной переменной скорости).

Теперь приведем строгое определение определенного интеграла.

Впервые для непрерывной функции оно было дано в 182 г. французским математиком Коши, а позднее немецкий математик Риман показал, что определение Коши применимо к более широкому классу функций [2, 22]. Это позволило ему впервые дать в общей форме определение интеграла и определить условие его существования.

Рассмотрим непрерывную на отрезке [a, b] функцию y = = f (x) (f (x) не обязательно положительна на [a, b]). Отрезок [a, b] разбивается на n частичных интервалов точками a = x0, x1,

x2, …, xn = b причем x0 < x1 < x2 <…< xn.

Во всех частичных интервалах [x0, x1], [x1, x2], …, [xn-1, xn] берутся произвольно точки М1, М2, …, Мn, находятся значения

функций y = f (x) в этих точках f (M1), f (M2), …, f (Mn). Составляем сумму вида

(5.7)

где Dxi = xi – xi-1.

Затем находим предел интегральной суммы (5.7) при стремлении к нулю длины наибольшего частичного интервала,

т. е. при max Dxi → 0.

(5.8)

16

В рассмотренной нами задаче о криволинейной трапеции предел (5.8) определяет ее площадь. В общем случае он называется определенным интегралом от функции f (x) в пределах от a до b и читается: интеграл от a до b f (x) по dx. Таким образом, согласно определению, получаем:

. (5.9)

Сумма в выражении (5.7) называется n-й интегральной суммой [2, 20, 22].

Как и в неопределенном интеграле f(x) — есть подынтегральное функция, f(x)dx — подынтегральное выражение, переменная х — переменная интегрирования, отрезок [a, b] называется интервалом интегрирования, а числа а и b нижним и верхним пределами соответственно.

Определенный интеграл есть некоторое число, а величина его зависит только от вида функции f(x) и от чисел а и b. Заметим, что площадь криволинейной трапеции — это геометрический смысл определенного интеграла. Вычисление определенного интеграла с помощью составления интегральных сумм вида (5.7) вызывает серьезные проблемы даже в самых простых случаях, поэтому для их нахождения используют другой способ, который мы рассмотрим ниже.

Теперь приведем без доказательства теорему существования определенного интеграла.

Теорема5.2.Если функция f(x) непрерывна в отрезке [a,b], то ее n-я интегральная сумма стремится к пределу при стремлении к нулю длины наибольшего частичного интервала. Этот предел, т. е. определенный интеграл

не зависит ни от способа разбиение [a, b] на частичные интервалы, ни от выбора в этих интервалах промежуточных точек [2].

164

Свойстваопределенногоинтеграла

1.Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций, т. е.

2.Постоянныймножительподынтегральнойфункцииможно выносить за знак интеграла, т. е.

. Если переставить местами пределы интегрирования, то интеграл изменит только знак, т. е.

.

4. Если интервал интегрирования [a, b] разбит на две части

[a, c] и [c, b], то

.

5.Если функция f(x) в интервале интегрирования не меняет знака, то интеграл представляет собой число того же знака, что и функция.

6.Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений функции f(x) на длину интервала интегрирования, т. е.

где M и m — соответственно наибольшее и наименьшее значения функции f (x) на отрезке [a, b] (см. рис. 5. ) [22].

165

Рис. 5.3

7. Если в каждой точке х отрезка [a, b] c(x) # f (x) # w (x), то

a < b.

8. Внутри интервала интегрирования [a, b] есть хотя бы одно значение х = А, для которого выполняется следующее равенство

ФормулаНьютона—Лейбница

Приведем без доказательства формулировку теоремы. Теорема 5.3. Значение определенного интеграла равно

разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интегриро-

вания [2, 22], т. е.

(5.10)

166

Или иначе, значение определенного интеграла равно приращению любой первообразной от подынтегральной функции в интервале интегрирования.

Формула (5.10) дает удобный способ вычисления определенных интегралов, если известна первообразная подынтегральной функции, т. е. необходимо найти любую первообразную подынтегральной функции и подставить в нее пределы интегрирования.

Приведем конкретные примеры.

Пример 5.17.

Пример 5.18.

Пример 5.19.

[Заметим, что d(x + 5) = dx]

167

Методинтегрированияпочастямвопределенноминтеграле

Формула интегрирования по частям в этом случае будет иметь вид:

(5.11)

Рассмотрим конкретные примеры.

Пример 5.20.

Пример 5.21.

168

Методзаменыпеременнойвопределенноминтеграле

Вычисление определенного интеграла методом замены переменной проводится так же, как и при нахождении неопределенного интеграла, за исключением того, что в данном случае нет необходимости возвращаться к первоначальной переменной. Но надо помнить, что, заменяя переменную под знаком интеграла, надо менять и пределы интегрирования.

Решим конкретные примеры.

Пример 5.22.

[Заметим, что d(x2 + 8) = 2xdx] = .

Делаем замену переменной, обозначим y = x2+8. Теперь необходимо поменять пределы интегрирования:

и окончательно получаем:

Пример 5.23.

[Заметим, что d(1 + x2) = 2xdx]

Теперь заменяем переменную и пределы интегрирования t = 1 + x2;

и окончательно получаем:

169

Пример 5.24.

[Заметим, что ]

Теперь делаем замену переменной и меняем пределы интегрирования tg x = t; в результате получаем:

5.3.некоторыесведенияонесобственныхинтегралах

Распространим понятие определенного интеграла на случай бесконечного интервала интегрирования.

Предположим, что функция y = f (x) непрерывна на интервале [a, +`). Тогда можно найти интеграл от функции f (x), который взят по любому интервалу [a, b], где b > a.

надо принять в качестве интеграла от функции f (x) в интервале [a, +`), чем больше b.

170