baldin_kv_red_matematika_dlia_gumanitariev

Если ненулевые элементы располагаются выше главной диагонали, то имеем верхнюю треугольную матрицу, а если ниже — нижнюю треугольную матрицу:

Матрица размера m 1 — это матрица-столбец, а матрица размера 1 n — матрица-строка:

Рассмотрим линейные операции над матрицами [1 , 19, 29] Для сложения двух матриц необходимо, чтобы они имели

одинаковые размеры.

Сумму двух матриц обозначим A + B, а ее элементы равны

aij + bij, т. е.

Например,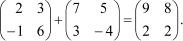

51

Сложение матриц обладает следующими свойствами:

1)A + B = B + A;

2)(A + B) + C = A + (B + C);

) Для любых двух матриц одинакового размера всегда существует единственная матрица Z такая, что A + Z = B. Тогда Z есть разность матриц B и A, т. е. Z = B – A. Элементы матрицы Z

равны bij – aij.

Произведением матрицы A = (aij) на число k [R называется матрица

Например,

Для умножения двух матриц необходимо, чтобы они были согласованными. Матрицы A и B называются согласованными, если число столбцов матрицы A равно числу строк матрицы B.

Пусть заданы матрицы:

Тогда произведением матрицы A на матрицу B называется матрица C размера m p, элементы cik которой находятся по формуле

52

Из определения произведения матриц следует, что

A E = E A = A.

Произведение матриц обладает следующими свойствами:

1)(A B) C = A (B C);

2)(A + B) C = AC + BC.

В общем случае A B B A.

Рассмотрим конкретный пример умножения двух матриц

Для квадратной матрицы размера n n вводится понятие определителя.

Определителем квадратной матрицы порядка n n (определителем порядка n) называется алгебраическая сумма всевозможных произведений элементов матрицы, взятых по одному из каждой строки, по одному из каждого столбца и снабженных знаками плюс и минус по некоторому определенному правилу. Это правило сформулируем позже [15, 29].

Определитель порядка n матрицы

обозначается следующим образом:

5

Приведем легко запоминающиеся правила для вычисления определителей второго и третьего порядков [ , 19]:

Например,

Сформулируем свойства определителей [ ,19].

1.При транспонировании матрицы ее определитель не меняется.

2.При перестановке строк (столбцов) знак определителя меняется на противоположный:

54

. Если все элементы строки (столбца) матрицы равны нулю, то ее определитель равен нулю:

то

4. Общий множитель всех элементов строки (столбца) определителя можно выносить за его знак:

где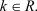

5. Определитель равен нулю, если все элементы минимум двух его строк (столбцов) пропорциональны:

где

6. Если каждый элемент строки (столбца) определителя есть сумма двух слагаемых, то такой определитель можно представить в виде суммы двух определителей, у одного из которых соответствующая строка (столбец) составлена из первых слагаемых суммы, а у другого — из вторых:

55

7. Значение определителя не изменится, если к элементам его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же вещественное число:

где

Дадим понятие минора и алгебраического дополнения [ , 19]. Рассмотрим матрицу размера m n:

Выделим в ней k различных строк и k различных столбцов, причем 1 # k # минимального значения из m и n.

Элементы выделенных строк и столбцов образуют квадратную матрицу порядка k. Определитель выделенной квадратной матрицы порядка k называют минором k-го порядка матрицы А.

Если в выделенную квадратную матрицу порядка k включены строки и столбцы исходной матрицы, имеющие одинаковые номера, то такой минор называется главным.

Полное обозначение минора k-го порядка следующее

где i — номера выделенных строк;

j — номера выделенных столбцов.

Общее число миноров порядка k прямоугольной матрицы размера m n можно найти по формуле

56

где — число сочетаний из m по k,

— число сочетаний из n по k.

Число миноров первого порядка совпадает с общим числом элементов исходной матрицы

Рассмотрим конкретный пример

Общее число миноров первого порядка данной матрицы А равно 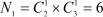. Например,

Максимальный порядок миноров данной матрицы равен двум.

Общее число миноров второго порядка равно

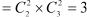. Например,

Рассмотрим теперь квадратную матрицу размера n n

Вычеркнем в ней все элементы i-й строки и j-го столбца. Оставшиеся элементы образуют квадратную матрицу размера (n–1) (n–1). Определитель этой матрицы будет минором (n–1) порядка исходной матрицы А.

57

Например, вычеркнем в матрице А первую строку и второй столбец и получим следующий минор (n–1) порядка исходной матрицы

Минор обозначаем по номеру элемента, который стоит на пересечении вычеркиваемой строки и вычеркиваемого столбца. В нашем случае это элемент a12.

Алгебраическим дополнением элемента aij квадратной матрицы порядка n называется число, вычисляемое по формуле: Aij = (–1)i+j Mij, т. е., если сумма номеров строки и столбца — четная, алгебраическое дополнение будет совпадать с соответствующим минором, а если нечетная, то алгебраическое дополнение и минор будут иметь разные знаки.

Используя понятие алгебраического дополнения можно сформулировать общее правило вычисления определителя n-го порядка. Он вычисляется с помощью формул разложения по элементам какой-либо строки или какого-либо столбца. Всего существует 2n формул разложения определителя (по элементам n-строк и n-столбцов) [ , 19, 29].

Например, приведем разложение по элементам первой строки и второго столбца:

То есть каждый элемент строки (столбца) умножается на соответствующее алгебраическое дополнение.

58

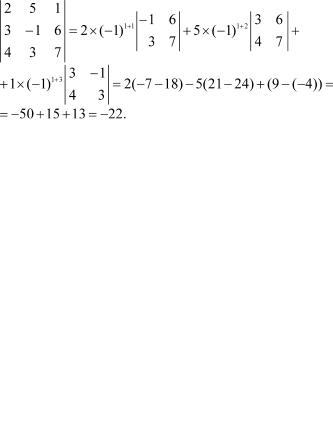
Теоретически с помощью формул разложения можно вычислить определитель квадратной матрицы любого порядка, но реально эти формулы используются для нахождения определителей не выше 4-го порядка. Объем вычислений можно несколько сократить, если использовать свойства определителей.

Из формул разложения следуют приведенные нами выше правила вычисления определителей второго и третьего порядков.

Рассмотрим конкретные примеры вычисления определителей.

В данном примере мы разложили определитель по элементам первой строки.

Найдем определитель 4-го порядка

К этому определителю сначала применим свойство номер 7. Первую строку определителя умножим последовательно на (–4); (– ); (–2) и сложим со 2-й; -й и 4-й строками. В результате получим

59

Полученный определитель разложим по элементам 1-ого столбца

К полученному определителю вновь применим свойство номер 7. Умножим последовательно третью строку на (–2) и на (–7) и сложим со второй и первой строчками. Получим

Последний определитель разложим по элементам первого столбца, т. е.

Теперь рассмотрим обратную матрицу и правило ее вычисления.

Квадратная матрица А называется вырожденной, если ее

определитель равен нулю, т. е. det A = 0.

В противоположном случае (det A 0) матрица А является невырожденной. А любой невырожденной матрице А соответствует единственная обратная матрица A–1.

Причем выполняется равенство

A–1 A = A A–1 = E

Приведем алгоритм нахождения обратной матрицы [1 , 19]. 1. Вычислить определитель матрицы А и убедиться, что он

не равен нулю.

60