Линейные дифференциальные уравнения первого порядка

Дифференциальные уравнения вида  называются линейными. Существуют несколько методов их решения: метод Бернулли, метод Лагранжа, метод интегрирующего множителя. Метод Бернулли Решение уравнения  ищется в виде . При этой замене получаем: . Функцию  выбирают из условия . Полученную функцию  подставляют в уравнение  (учитываем ), решая которое находят функцию .

№1

br> Решить уравнение . Данное уравнение линейное.  Полагая  и учитывая , получим . Преобразуем полученное уравнение: . Функцию  выберем из условия . Учитывая , получаем ; ; . Интегрируем это равенство:  ( см. примечание).  Подставляя полученный результат  в уравнение , и учитывая, что при , получим . Сократим последнее равенство на  и учтем . Тогда , Учитывая , ответ будет таким: . Примечание При интегрировании равенства , получается результат ,, откуда следует, что , или ,. Однако в методе Бернулли нас интересует не все множество функций , а лишь одна функция из этого множества. Проще всего принять , и выбрать ,, тогда .

№2

Решить уравнение . Покажем, что данное уравнение относится к линейным. Для этого обе части разделим на коэффициент при . Получили уравнение вида , т.е. линейное. Делаем замену : . Выносим  за скобки: . Согласно методу Бернулли функцию  необходимо выбрать так, чтобы . Учтем  и разделим переменные в уравнении: . Интегрируя последнее равенство учтем : . Возвращаясь к уравнению , учитывая  при , получаем: , откуда , следовательно . Так как .ъ

Пример 3

Построить область интегрирования и изменить порядок интегрирования

Решение: По условию дан первый способ обхода области. Решение опять начинается с чертежа. Здесь область  не лежит на блюдечке с голубой каёмочкой, но построить её не составляет особого труда. Сначала «снимаем» функции с пределов интегрирования: ,. Функция , понятно, задаёт прямую, но что задаёт функция ?  Давайте её немного преобразуем:  – окружность с центром в начале координат радиуса 2. Функция же  задаёт верхнюю полуокружность (не забываем, что если есть сомнения, то всегда можно подставить точку лежащую на верхней или нижней полуокружности).

Смотрим на пределы внешнего интеграла: «икс» изменяется от –2  до 0.

Выполним чертёж: Для наглядности я указал стрелками первый способ обхода области, который соответствует повторным интегралам условия: .

Теперь нужно изменить порядок обхода области, для этого перейдем к обратным функциям (выразим «иксы» через «игреки»): Недавно мы преобразовали функцию  к уравнению окружности , далее выражаем «икс»:  В результате получаем две обратные функции:  – определяет правую полуокружность;  – определяет левую полуокружность. Опять же, если возникают сомнения, возьмите любую точку окружности и выясните, где лево, а где право.

Изменим порядок обхода области:

Согласно второму способу обхода, лазерный луч входит в область слева через левую полуокружность  и выходит справа через прямую  (красная стрелка). В то же время лазерная указка проводится вдоль оси ординат снизу вверх от 0 до 2 (зелёная стрелка).

Таким образом, порядок обхода области:

В общем-то, можно записать ответ: 

Пример 11

С помощью двойного интеграла, вычислить площадь плоской фигуры , ограниченной линиями , 

Решение: нас с нетерпением ждут две параболы с бзиком, которые лежат на боку. Улыбаться не нужно, похожие вещи в кратных интегралах встречаются частенько.

Как проще всего сделать чертёж?

Представим параболу  в виде двух функций:  – верхняя ветвь и  – нижняя ветвь.

Аналогично, представим параболу  в виде верхней  и нижней  ветвей.

Далее рулит поточечное построение графиков, в результате чего получается вот такая причудливая фигура:

Площадь фигуры вычислим с помощью двойного интеграла по формуле:

Что будет, если мы выберем первый способ обхода области? Во-первых, данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину: . Интегралы, конечно, не сверхсложного уровня, но… существует старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.

Поэтому из недоразумения, которое дано в условии, выразим обратные функции: Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без всяких там листьев, желудей веток и корней.

Согласно второму способу, обход области будет следующим:

Таким образом: Как говорится, ощутите разницу.

1) Расправляемся с внутренним интегралом:

Результат подставляем во внешний интеграл:

2)

Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней. Хотя кто прочитал второй параграф урокаКак вычислить объем тела вращения, тот уже не испытывает ни малейшей неловкости с интегрированием по «игрек».

Также обратите внимание на первый шаг: подынтегральная функция  является чётной, а отрезок интегрирования симметричен относительно нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Данный приём подробно закомментирован на урокеЭффективные методы вычисления определённого интеграла.

Что добавить…. Всё!

Ответ: 

Для проверки своей технике интегрирования можете попробовать вычислить . Ответ должен получиться точно таким же.

Пример 4: Решение: Перейдём к прямым функциям: Выполним чертёж: Изменим порядок обхода области: Ответ: 

Изменить порядок интегрирования в повторном интеграле .

Решение.

Кривые  и отрезок прямой x = 2 ограничивают область G, изображенную на Рис. 1, а.

Данный повторный интеграл равен двойному интегралу по этой области. Чтобы изменить порядок интегрирования в повторном интеграле, нужно разбить область G на три части, как показано на Рис. 1, б. Кривая  является верхней полуокружностью окружности (x - 1)² + y² = 1. Разрешая это уравнение относительно x, получим два решения: . В областях G₁ и G₂ переменная y изменяется от 0 до 1, а при каждом значении y переменная x изменяется в области G₁ от y²/2 (значение x на кривой ) до  (значение x на окружности), а в области G₂- от  до 2. Поэтому по формуле  получаем

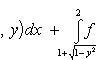
Аналогично для области G₃ имеем

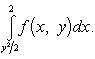
Таким образом, окончательно находим

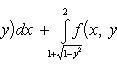
Таблица основных формул дифференцирования

Функция	Производная	Функция	Производная

       Примечание: Символами  обозначаются гиперболические функции: гиперболический синус , гиперболический косинус , гиперболический тангенс  и котангенс . Определяются они по формулам:

Линейные дифференциальные уравнения первого порядка

Дифференциальные уравнения вида  называются линейными. Существуют несколько методов их решения: метод Бернулли, метод Лагранжа, метод интегрирующего множителя. Метод Бернулли Решение уравнения  ищется в виде . При этой замене получаем: . Функцию  выбирают из условия . Полученную функцию  подставляют в уравнение  (учитываем ), решая которое находят функцию .

№1

br> Решить уравнение . Данное уравнение линейное.  Полагая  и учитывая , получим . Преобразуем полученное уравнение: . Функцию  выберем из условия . Учитывая , получаем 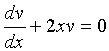; ; . Интегрируем это равенство:  ( см. примечание).  Подставляя полученный результат  в уравнение , и учитывая, что при , получим . Сократим последнее равенство на  и учтем . Тогда , Учитывая , ответ будет таким: . Примечание При интегрировании равенства , получается результат ,, откуда следует, что , или ,. Однако в методе Бернулли нас интересует не все множество функций , а лишь одна функция из этого множества. Проще всего принять , и выбрать ,, тогда .

№2

Решить уравнение . Покажем, что данное уравнение относится к линейным. Для этого обе части разделим на коэффициент при . Получили уравнение вида , т.е. линейное. Делаем замену : . Выносим  за скобки: . Согласно методу Бернулли функцию  необходимо выбрать так, чтобы . Учтем  и разделим переменные в уравнении: 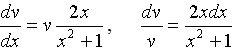. Интегрируя последнее равенство учтем : . Возвращаясь к уравнению , учитывая  при , получаем: , откуда , следовательно . Так как .

Дифференциальные уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется дифференциальное уравнение первого порядка вида  или . Пример Решить уравнение . В частности, найти решение, удовлетворяющее начальному условию . Учитывая, что  и вынося за скобки , получим , или, что то же самое, . Разделив обе части уравнения на произведение  получим: . Интегрируем обе части последнего равенства: . Учитываем то, что  и сокращаем обе части равенства на . Произвольную постоянную  удобно представить в виде . Тогда , откуда и получаем ответ . Учтем заданное условие . Следовательно, искомое частное решение есть .

Однородные дифференциальные уравнения

Дифференциальное уравнение  называется однородным, если  – однородная функция нулевой степени.  Дифференциальное уравнение первого порядка в симметричной форме  является однородным, если  – однородные функции одной степени.  Замена  приводит однородное уравнение к уравнению с разделяющимися переменными.  Пример Решить уравнение . Найти решение, удовлетворяющее начальному условию . Данное уравнение однородное. Произведя замену , получим  (здесь мы учли, что ). Сокращаем на . Учитывая, что , получим . Интегрируем полученное равенство: . Обозначая  и учитывая , получаем ответ . Для данного начального условия . Следовательно, искомое частное решение есть .

Линейные дифференциальные уравнения первого порядка

Дифференциальные уравнения вида  называются линейными. Существуют несколько методов их решения: метод Бернулли, метод Лагранжа, метод интегрирующего множителя.  Метод Бернулли Решение уравнения  ищется в виде . При этой замене получаем: . Функцию  выбирают из условия . Полученную функцию  подставляют в уравнение  (учитываем ), решая которое находят функцию . Пример Решить уравнение . Полагая  и учитывая , получим . Преобразуем полученное уравнение: . Функцию  выберем из условия . Учитывая , получаем . Интегрируем это равенство:  ( см. примечание).  Подставляя полученный результат  в уравнение , и учитывая, что при  , получим . Сократим последнее равенство на  и учтем . Тогда . Учитывая , ответ будет таким: . Примечание При интегрировании равенства , получается результат , откуда следует, что  или . Однако в методе Бернулли нас интересует не все множество функций , а лишь одна функция из этого множества. Проще всего принять  и выбрать , тогда .

Основные тригонометрические формулы

Формулы тригонометрических функций суммы и разности двух аргументов

 

Формулы тригонометрических функций двойных, тройных и половинных аргументов

 

Формулы суммы и разности тригонометрических функций

 

Дополнительные формулы

 

Основные значения тригонометрических функций углов I четверти

   

Знаки тригонометрических функций

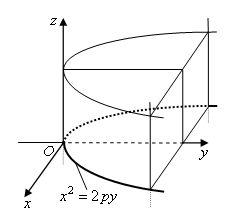
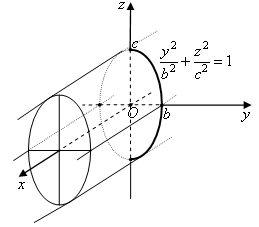
Поверхности второго порядка

Триосний эллипсоид	Однопорожнинний гиперболоид	Двопорожнинний гиперболоид

Эллиптическая параболоида	Гиперболический параболоид	Эллиптический конус

Параболический цилиндр	Гиперболический цилиндр	Эллиптический цилиндр

Элементарные функции