Решение типового варианта.

Часть 1 Линейная алгебра. Аналитическая геометрия

Задача 1.

Вычислить определитель .

Решение.

Способ 1.

Вычислим определитель методом понижения порядка.

Выносим за знак определителя из четвертого столбца общий множитель :

,

, а затем будем последовательно умножать третью строку на и складывать соответственно с первой и со второй строками. Имеем

.

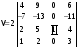Далее полученный определитель раскладываем по элементам третьего столбца

.

Получим определитель третьего порядка, который можно вычислить по правилу Саррюса или подобным приемом свести к вычислению одного определителя второго порядка. Для этого последовательно умножим элементы первого столбца на и прибавим соответственно к элементам второго и третьего столбцов. Получаем

.

Полученный определитель раскладываем по элементам третьей строки, имеем:

.

Способ 2.

Вычислим определитель методом приведения его к треугольному виду.

Выполним следующие операции. Выносим за знак определителя из четвертого столбца общий множитель , а затем переставим местами первую и четвертую строки – определитель меняет свой знак на противоположный:

.

Далее, первую строку определителя сложим со второй, эту же строку, умноженную на с третьей, на с четвертой строкой. В итоге получим определитель, который равен исходному:

.

Вторую строку определителя умножим на и сложим с третьей:

.

Из четвертой строки вычтем третью:

.

Определитель треугольного вида равен произведению элементов его главной диагонали. Имеем

.

Задача 2.

Даны матрицы и . Найдите матрицу , если

.

Решение.

.

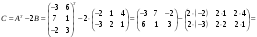
Задача 3.

Какое из произведений существует или 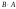? Почему? Найдите это произведение, если

.

Решение.

Произведение матриц определено только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведение матриц содержит столько строк, сколько имеет первая матрица, и столько столбцов, сколько имеет вторая матрица. Для заданных матриц определено только произведение .

.

Задача 4.

Решите систему уравнений тремя способами:

1. по формулам Крамера;

2. с помощью обратной матрицы (матричным методом);

3. методом Жордана - Гаусса.

Выполните проверку.

Решение.

1) Если определитель системы линейных алгебраических уравнений отличен от нуля, то система имеет единственное решение, которое может быть найдено по формулам Крамера

,

где определитель системы,

вспомогательные определители, которые получаются из определителя заменой столбца из коэффициентов соответственно при столбцом свободных членов.

Определитель системы равен

.

Вычислим вспомогательные определители:

;

;

.

По формулам Крамера найдем:

2) Систему линейных алгебраических уравнений можно записать в виде матричного уравнения:

,

где матрица системы; столбец неизвестных; столбец свободных членов.

Если матрица невырожденная, то решение системы определяется по формуле:

,

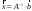где обратная матрица.

Для данной системы

столбец неизвестных , столбец свободных членов .

Найдем обратную матрицу по формуле

,

где определитель матрицы ,

союзная матрица, которая получается из матрицы заменой всех ее элементов соответствующими им алгебраическими дополнениями.

Определитель матрицы

.

Вычислим алгебраические дополнения для элементов матрицы по формуле

,

где минор элемента .

, , ,

, , ,

, , .

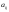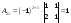Составим союзную матрицу

.

Обратная матрица будет равна

,

.

Проверим правильность нахождения обратной матрицы, используя соотношение .

.

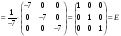Теперь можно получить решение системы в матричном виде:

.

.

3) Метод Жордана – Гаусса (метод полного исключения неизвестных).

Пусть задана СЛАУ . Запишем ее расширенную матрицу . Каждому элементарному преобразованию строк расширенной матрицы соответствует аналогичное преобразование уравнений в исходной СЛАУ.

Элементарные преобразования в расширенной матрице:

1. перемена местами строк;

2. перемена местами столбцов с запоминанием, какому неизвестному соответствует каждый столбец;

3. умножение (деление) строки на ненулевую постоянную;

4. прибавление к любой строке линейную комбинацию других строк;

5. вычеркивание одной из двух пропорциональных (равных) строк;

6. вычеркивание нулевой строки.

Эти преобразования не меняют множество решений системы.

Если элементарными преобразованиями строк матрица переведена в матрицу , то столбец 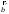есть решением системы линейных уравнений .

Составим расширенную матрицу и проведем необходимые элементарные преобразования:

.

.

Проверка.

Подставив полученное решение в систему, убедимся в правильности полученного решения:

Задача 5.

Найдите общее решение, построив фундаментальную систему для однородной системы алгебраических уравнений.

Решение.

Составим матрицу однородной СЛАУ и проведем необходимые элементарные преобразования строк

.

, где число неизвестных. Система имеет нетривиальные решения. Базисный минор . Число свободных переменных . Пусть базисные переменные, 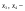свободные переменные.

Исходная система равносильна системе из двух уравнений

Общее решение:

.

Полагая и , из общего решения получим фундаментальную систему решений (Ф.С.Р.):

.

Общее решение системы имеет вид

.

Задача 6.

Исследовать на совместность и в случае совместности найдите общее решение методом Жордана – Гаусса и одно частное решение системы. Выполните проверку.

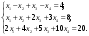
Решение.

Используем метод Жордана – Гаусса (метод полного исключения). Составим расширенную матрицу неоднородной СЛАУ и проведем необходимые элементарные преобразования строк:

.

, где число неизвестных. Система совместна, имеет бесчисленное множество решений. Базисный минор . Число свободных переменных . Пусть базисные переменные, свободные переменные.

Исходная система равносильна системе из двух уравнений

Общее решение неоднородной СЛАУ представим так:

.

Полагая, например, , найдем частное решение:

.

Непосредственной подстановкой в систему частного решения убедимся в его правильности:

Задача 7.

Найдите координаты, модуль и направляющие косинусы вектора , его орт, если .

Решение.

Найдем координаты вектора :

;

.

Длина вектора определяется так:

или ;

.

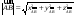Направляющие косинусы вектора определяется по следующим формулам:

.

Следовательно,

.

Вектор является ортом (единичным вектором) вектора .

.

Задача 8.

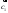Вычислите скалярное и векторное произведения векторов , если . Являются ли векторы и коллинеарными? Являются ли векторы и ортогональными?

Решение.

.

.

Скалярное произведение:

;

.

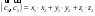Векторное произведение:

;

.

Условие коллинеарности векторов и :

векторы не коллинеарны.

Условие ортогональности векторов и :

векторы не ортогональны.

Задача 9.

Заданы вершины треугольника . Вычислите его площадь и косинус внутреннего угла .

Решение.

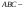Внутренний угол в треугольнике это угол между векторами и . Здесь

, .

;

.

Площадь треугольника вычисляется по формуле

.

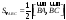Вычислим векторное произведение векторов и :

.

Тогда площадь треугольника

.

Задача 10.

Выясните, образуют ли векторы базис. Если образуют, то разложите вектор по этому базису.

.

Решение.

Поскольку определитель , векторы не компланарны, следовательно, линейно независимые.

Найдем координаты вектора в базисе . Запишем

, или .

Это векторное равенство равносильно системе линейных уравнений:

Методом Жордана – Гаусса решим систему:

.

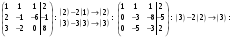
Таким образом, .

Задача 11.

Вычислите площадь параллелограмма, построенного на векторах и , если .

Решение.

Площадь параллелограмма, построенного на векторах и , равна

.

Согласно свойствам векторное произведение векторных многочленов производится по тем же правилам, что и умножение алгебраических многочленов. Тогда, используя антикоммутативность векторного произведения и тот факт, что векторное произведение вектора на самого себя равно нуль – вектору, получим

.

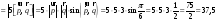Задача 12.

Вычислить , если .

Решение.

.

Задача 13.

Найти вектор , ортогональный векторам и и удовлетворяет условию .

Решение.

Вектор коллинеарен векторному произведению , следовательно, . Поскольку

,

то

.

Так как , то

,

,

.

Теперь можно определить координаты вектора

.

Задача 14.

Принадлежат ли точки и одной плоскости?

Решение.

Точки и лежат в одной плоскости, если векторы и компланарны. Найдем координаты этих векторов:

;

;

,

.

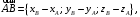
Проверим их компланарность

,

.

Точки и лежат в одной плоскости.

Задача 15.

Заданы прямая 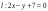и точка . Запишите:

1) уравнение прямой, проходящей через точку параллельно прямой ;

2) уравнение прямой, проходящей через точку 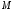перпендикулярно прямой .

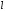Решение.

Преобразуем общее уравнение данной прямой в уравнение с угловым коэффициентом

.

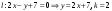1) Так как искомая прямая параллельна данной, то ее угловой коэффициент равен угловому коэффициенту данной прямой, следовательно, . Тогда по точке и угловому коэффициенту составляем уравнение прямой

,

,

.

2) С учетом условия перпендикулярности прямых угловой коэффициент искомой прямой . Тогда по точке и угловому коэффициенту составляем уравнение прямой

,

,

.

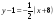Задача 16.

Напишите уравнение прямой, которая проходит через точку и через точку пересечения прямых .

Решение.

Для нахождения координат точки пересечения прямых и составляем систему уравнений

Решая ее, получаем .

Теперь по двум известным точкам и составляем уравнение искомой прямой:

,

,

,

,

.

Задача 17.

Даны вершины треугольника . Найти:

1. уравнение стороны 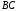и длину ;

2. уравнение высоты, опущенной из вершины на сторону ;

3. уравнение медианы, проведенной из вершины .

Решение.

1. Воспользовавшись уравнением прямой, проходящей через две точки, получим уравнение стороны :

,

,

,

,

.

Расстояние между точками и определяется по формуле:

,

.

2. С учетом перпендикулярности прямых и угловой коэффициент высоты . Преобразуем общее уравнение прямой в уравнение с угловым коэффициентом

.

По точке и угловому коэффициенту составляем уравнение высоты :

,

,

.

3. По известным формулам находим координаты середины отрезка :

;

.

Теперь по двум известным точкам и составляем уравнение медианы :

,

,

,

.