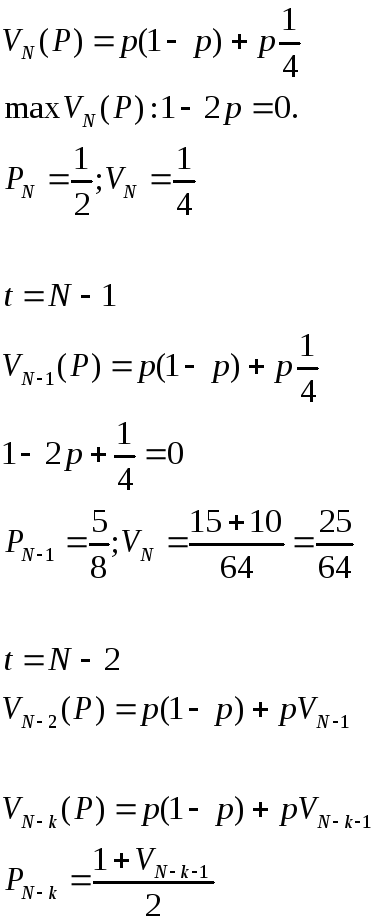3. Автономные системы
Поведение автономных систем задается разностным уравнением:
![]() (1)
(1)
Автономные системы – модели ситуаций, где поведение изменяется с t, а структура системы остается неизменной.
Это дает возможность использовать для анализа системы графические методы.
В общем случае:
![]() (2)
(2)
Функция d(.)
показывает. Насколько изменится состояние
системы, от периода к периоду. Каждой
точке х можно сопоставить вектор
![]() в соответствии с уравнением (2). Функцияd(.)
в этом контексте называется также
векторным полем.
в соответствии с уравнением (2). Функцияd(.)
в этом контексте называется также
векторным полем.
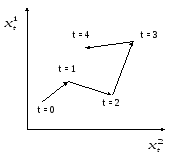

Для автономных систем:


В автономных
системах все системы попавшие когда –
либо в точку
![]() в последствии следуют одной и той же
траектории.
в последствии следуют одной и той же
траектории.
В неавтономных
системах поведение зависит также от
того, когда система попала в точку
![]() .
.
При начальном
условии
![]() для автономных систем применяем уравнение
(1)
для автономных систем применяем уравнение
(1)

В вышеприведенной
системе
![]() означает результатt-кратного
итеративного применения функции
означает результатt-кратного
итеративного применения функции
![]() к своему аргументу.
к своему аргументу.
В уравнении
![]() функция
функция![]() иногда называется потоком системы.
иногда называется потоком системы.
4.Устойчивые состояния, периодические равновесия и стабильность.
Для многих
динамических систем характерно то, что
с течением времени система переходит
в устойчивое состояние. Поэтому нас
часто будет интересовать асимптотическое
поведение системы при
![]() .
.
Рассмотрим систему
![]()
![]()
Следовательно,
если
![]() существует, то
существует, то![]()
Устойчивое состояние
(стационарное или неподвижная точка):
точка
![]() называется устойчивым состоянием
системы
называется устойчивым состоянием
системы![]() или неподвижной точкой отображения
или неподвижной точкой отображения![]() ,
если
,
если![]() .
.
Неподвижные точки широко используются для изучения долговременного поведения экономических систем.
Пример:
![]()
Неподвижная точка:

Устойчивое состояние
![]() динамической системы
динамической системы![]() называется стабильным, если любая
траектория, проходящая возле
называется стабильным, если любая
траектория, проходящая возле![]() остается
вблизи
остается
вблизи![]() .
.
Точка
![]() называется стабильной (по Ляпунову),
неподвижной точкой отображения
называется стабильной (по Ляпунову),
неподвижной точкой отображения![]() ,
если для любого
,
если для любого![]() существует такое число
существует такое число![]() ,
что
,
что![]() .
.


Асимптотическая устойчивость.
Точка
![]() называется
асимптотически устойчивой, если она
стабильна по Ляпунову и, коме того, если
называется
асимптотически устойчивой, если она
стабильна по Ляпунову и, коме того, если![]() для любогоs
для любогоs
![]() .
.
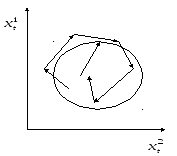





Периодическим
решением динамической системы
![]() называется решение в форме:
называется решение в форме:![]() ,
где р – период орбиты.
,
где р – период орбиты.
Пример:
![]()


Скалярные линейные системы.
Имеют следующую формулу:
![]() (1)
(1)
Если в уравнении
(1)
![]() ,
то (1) – однородное уравнение.
,
то (1) – однородное уравнение.
Однородные линейные системы.
t![]() (2)
(2)
Фазовая диаграмма
– график зависимости
![]()
Случай 1:
![]()
t =
1
![]()
![]()
![]()

В этом случае
![]() асимптотически.
асимптотически.
Случай 2:
![]()


В этом случае в
системе будут происходить периодические
колебания (осцилляции), затухающие со
временем
![]() .
.
Случай 3:
![]()


В этом случае имеет место неограниченный рост системы.
Случай 4:
![]()
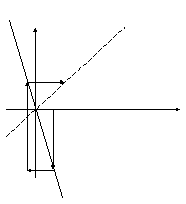

В этом случае в системе имеют место расходящиеся колебания с возрастающей амплитудой.
Оставшиеся возможности:
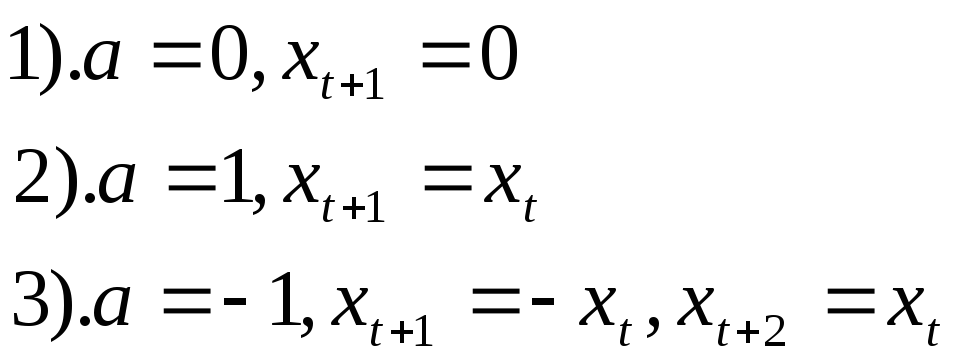
Общее решение:
![]() (3)
(3)
Если

При
![]()
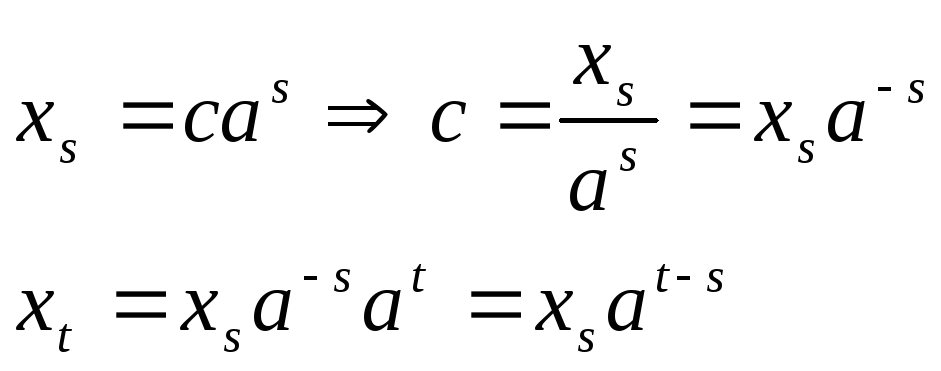
Неоднородные линейные системы.
![]() (1)
(1)
При анализе неоднородных систем важную роль играет т.н. принцип суперпозиции. Заключается он в следующем:
Общее решение уравнения (1) м.б. записано в форме:
![]() (2)
(2)
где
![]() комплементарная функция (общее решение
однородного уравнения).
комплементарная функция (общее решение
однородного уравнения).
![]() любое
частное решение уравнения (1).
любое
частное решение уравнения (1).
Доказательство:
1. Если
![]() - решение уравнения (1), то
- решение уравнения (1), то![]() тоже будет решением уравнения (1).
тоже будет решением уравнения (1).
Если
![]() - решение уравнения (1), то
- решение уравнения (1), то![]()
Если
![]() - другое решение (1), то
- другое решение (1), то

2. Мы показали, что
если мы начнем с какого – либо решения
![]() и добавим к нему
и добавим к нему![]() ,
то мы получим другое решение уравнения
(1). Возникает вопрос, получим ли мы
подобным образом все решения уравнения
(1).
,
то мы получим другое решение уравнения
(1). Возникает вопрос, получим ли мы
подобным образом все решения уравнения
(1).
Докажем, что это действительно так:
Пусть у нас есть
2 решения этого уравнения:
![]() и
и![]()
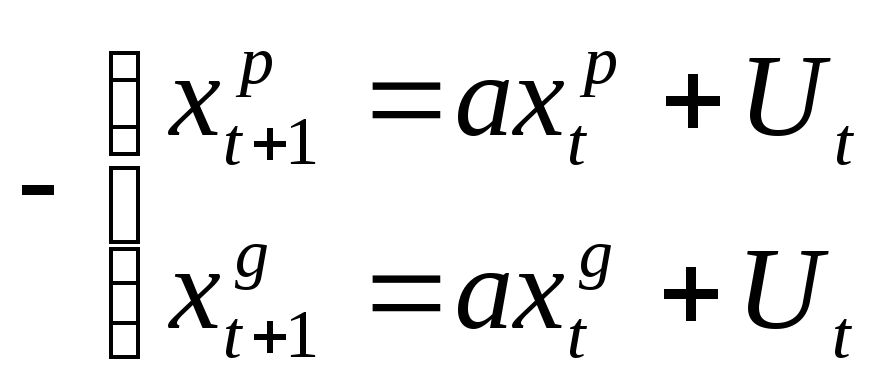
![]() - однородное
уравнение
- однородное
уравнение
![]() - общее
решение =
- общее
решение =
![]()
![]() ,
ч.т.д.
,
ч.т.д.
Автономные линейные системы.
Автономные линейные уравнения имеют вид:
![]() (3)
(3)
![]()
![]() (решение уравнения
(решение уравнения
![]() )
)
В качестве частного решения уравнения (3) выберем устойчивое состояние системы (3) или т.н. стационарное решение.
Стационарное
решение
![]() найдем как неподвижную точку (3):
найдем как неподвижную точку (3):
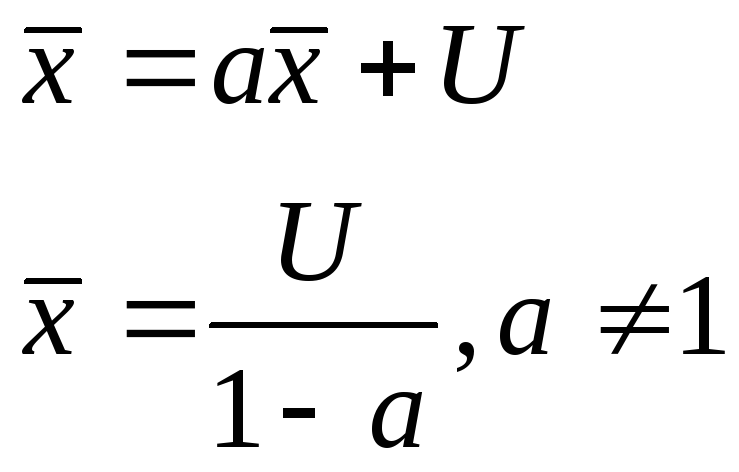
Общее решение уравнения (3) будет иметь вид:
![]() (4)
(4)
Если
![]() ,
то
,
то![]()
В случае, когда
![]() с течением времени система достигнет
состояния
с течением времени система достигнет
состояния![]() и соответствующим подбором управления,
мы сможем достигнуть любого возможного
состояния. Система (3) называется в этом
случае управляемой.
и соответствующим подбором управления,
мы сможем достигнуть любого возможного
состояния. Система (3) называется в этом
случае управляемой.
Если
![]() , то
, то![]() ,
т.е. система примет неограниченные
значения вне зависимости от управления,
т.е. в этом случае система (3) будет
неуправляема.
,
т.е. система примет неограниченные
значения вне зависимости от управления,
т.е. в этом случае система (3) будет
неуправляема.
Формула (4) дает нам общее решение. Но нас также интересует частное решение в случае. Если нам известно состояние системы в момент t = S:

Частное решение:
![]() (5)
(5)
Рассмотрим вопрос об устойчивости решений автономных линейных систем:
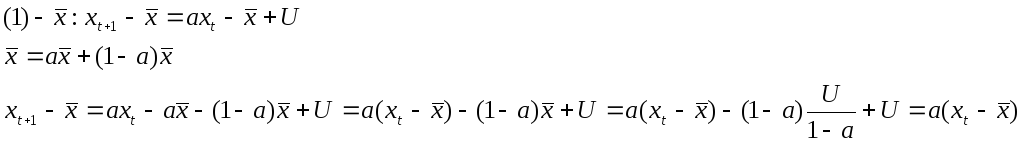
![]()
Если
![]() ,
то
,
то![]()
В том случае, когда при применении некоторого отображения расстояние между двумя точками сокращается, такое отображение называется сжимающим.
Если
![]() ,
то
,
то![]()
И отображение – растягивающее, система (3) будет асимптотически неустойчивой.
Неавтономные системы.
![]() (1)
(1)
Прямое решение:
![]() (2)
(2)
Если задано начальное состояние:
![]()
(2) называется прямым решением системы (1)
При
![]() :
:
![]()
Если
![]() (как для автономных систем), тогда
(как для автономных систем), тогда
![]()
Если существует
число U,
такое, что уравнение на любом периоде
времени
![]() ,
то
,
то![]()
Для того, чтобы прямое решение системы (1) асимптотически сходилось к устойчивому состоянию требуется, чтобы:
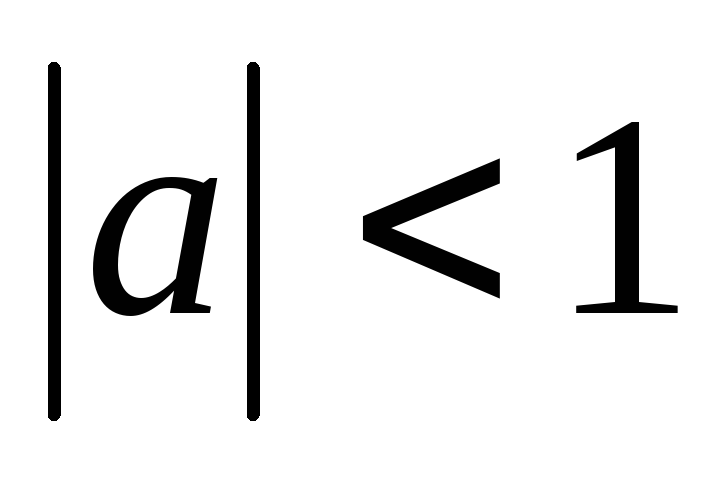
Последовательность
 должна быть ограничена сверху.
должна быть ограничена сверху.
Обозначим:
![]()
Если
![]() ,
то система асимптотически неустойчива
и с течением времени приобретает
неограниченные значения.
,
то система асимптотически неустойчива
и с течением времени приобретает
неограниченные значения.
Обратное решение:
Сдвинем:
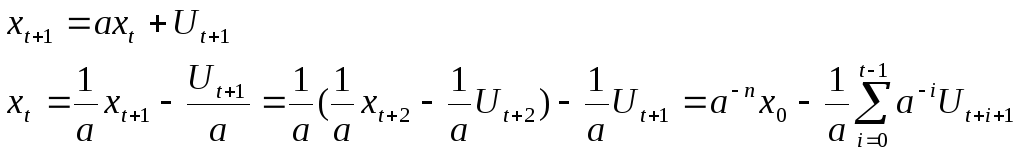
Если
![]() ,
то
,
то![]() ,
тогда
,
тогда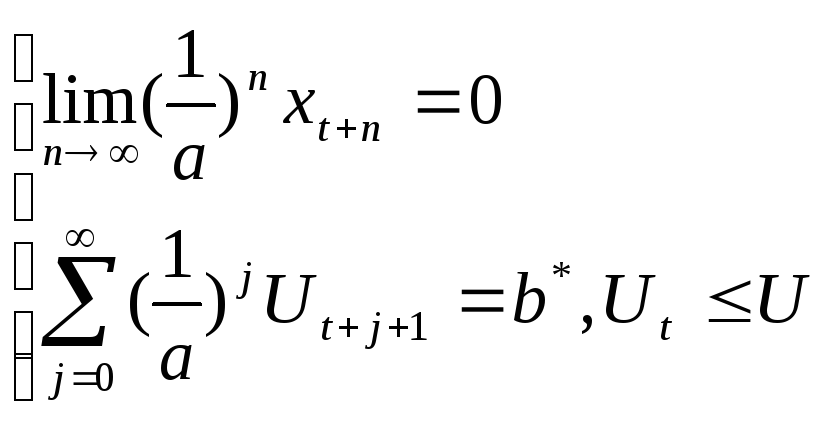
В этом случае обратное решение будет асимптотически устойчивым.
Таким образом, либо прямое, либо обратное решение является асимптотически устойчивым.
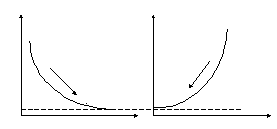

Динамика цен на акции на фондовых биржах.
Предположим, что
![]() - стоимость акций в моментt,
- стоимость акций в моментt,
![]() - последовательность
дивидендов по акции (считаем известными)
- последовательность
дивидендов по акции (считаем известными)
![]() ожидаемая цена
акции в следующем периоде.
ожидаемая цена
акции в следующем периоде.
r – фиксированная процентная ставка по банковским вкладам.
Принцип отсутствия арбитража состоит в том, что на рынке не должно быть ситуаций, позволяющих получать немедленную прибыль без риска (подобные ситуации называются «арбитражи»).
Инвестируем
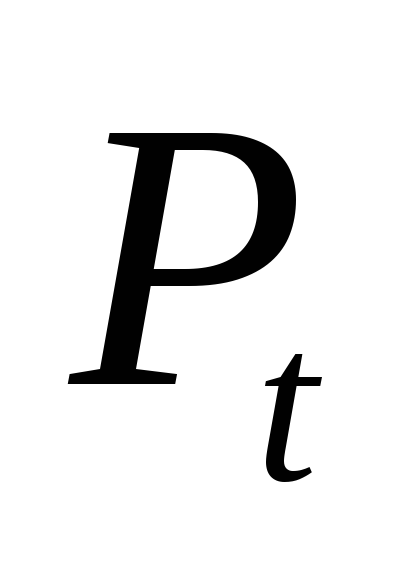 в банк, получаем
в банк, получаем
Покупаем акцию за
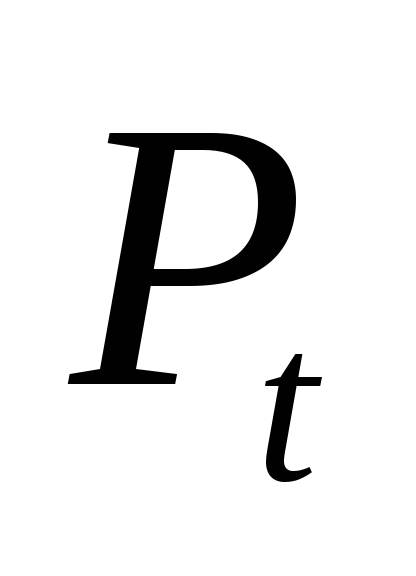 ,
получаем
,
получаем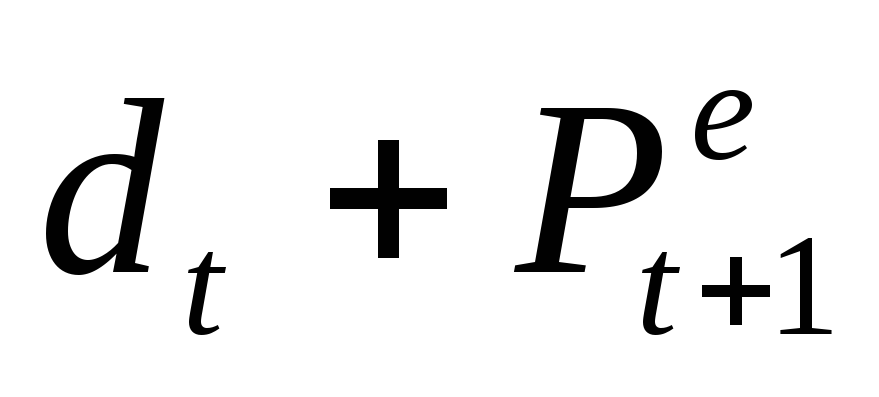
По принципу
арбитража:
![]()
Модель адаптивных ожиданий.
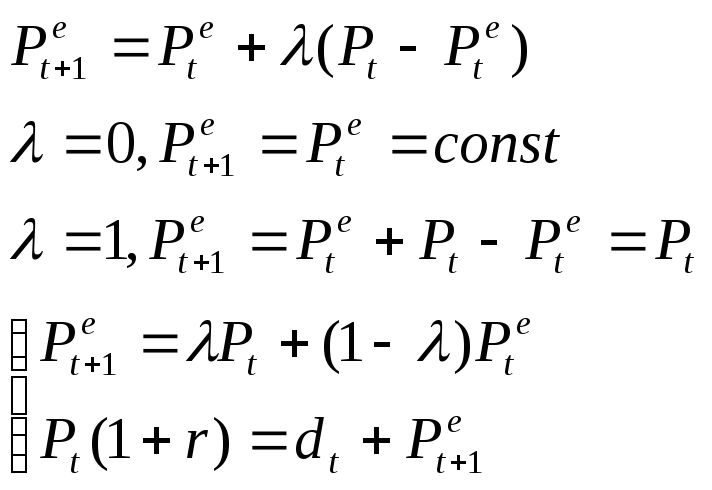
Подставим второе уравнение в первое:

Пусть
![]()

Предположим,
![]()
![]()
Найдем
![]() для этого найдем неподвижную точку:
для этого найдем неподвижную точку:
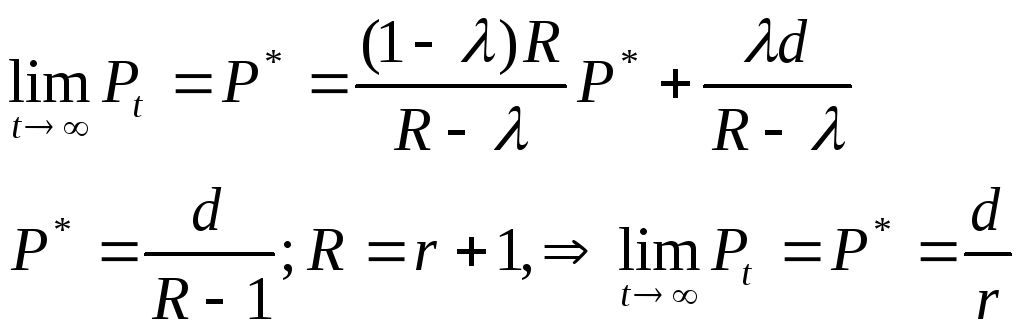
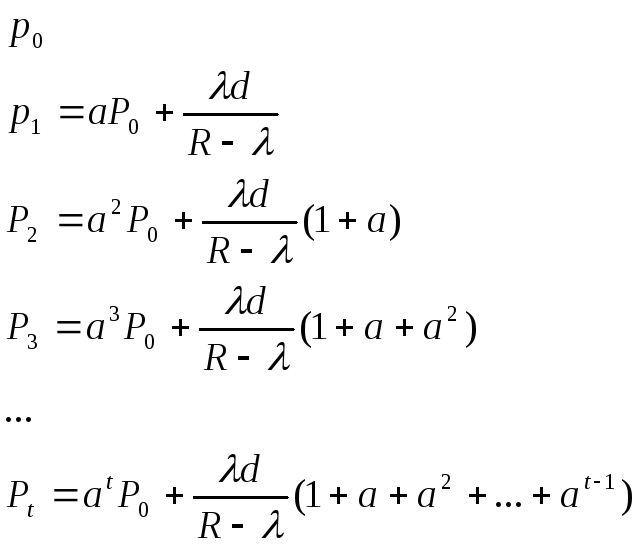


![]()
Модель с полным предвидением.
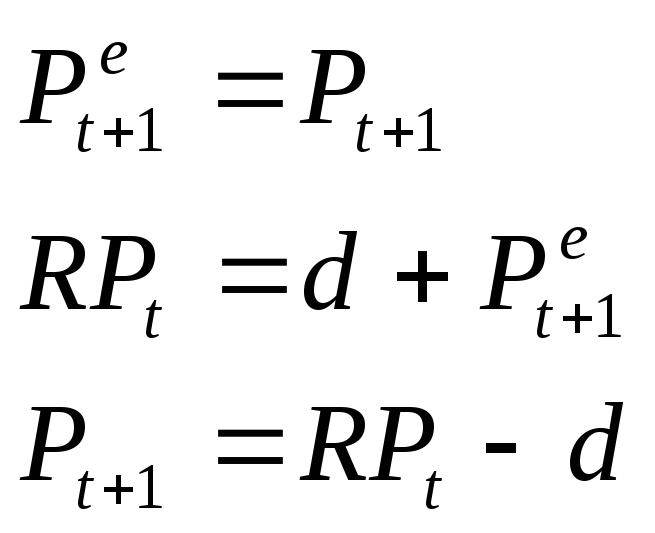
Неподвижная точка:

Модель поведения акций, при которой цены акций с течением времени неограниченно возрастают, называется финансовой пирамидой.
![]()
В модели полного предвидения ожидания инвесторов играют роль «самовыполняющегося пророчества»: цены на акции могут неограниченно расти, потому что инвесторы считают, что они будут расти.
Альтернативой моделей адаптивных ожиданий и полного предвидения является т.н. модель рациональных ожиданий, в которой предполагается, что оценка акций в следующем периоде является математическим ожиданием от стоимости акций в следующем периоде:
![]()
В этом случае прогнозы инвесторов представляют собой несмещенную оценку будущей стоимости акций.
![]()
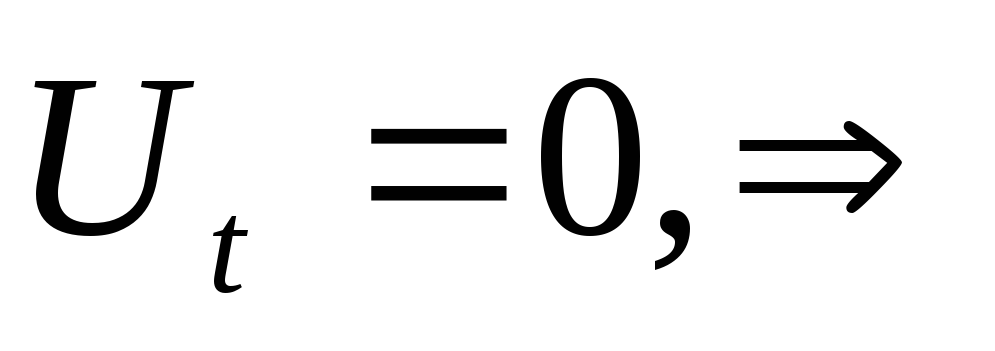 однородные линейные
скалярные системы. Решение:
однородные линейные
скалярные системы. Решение:
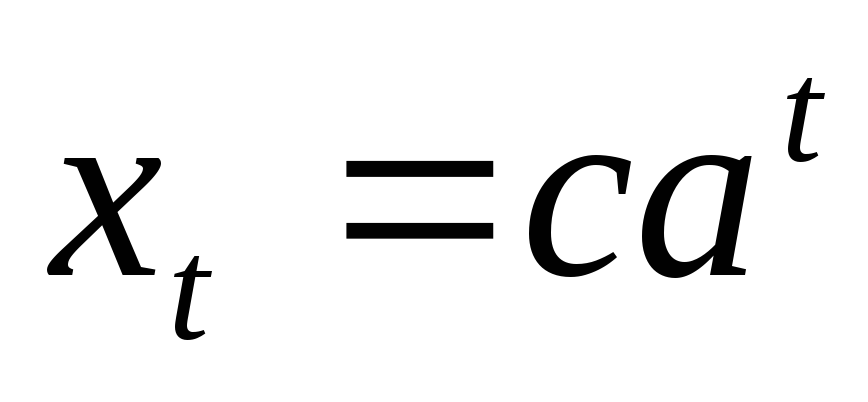
 линейные скалярные
автономные системы.
линейные скалярные
автономные системы.
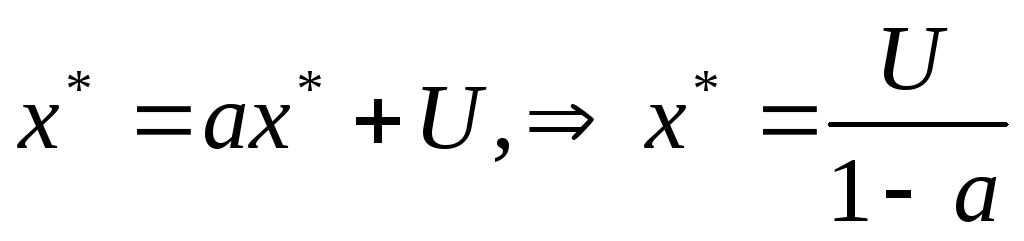 .
Решение:
.
Решение: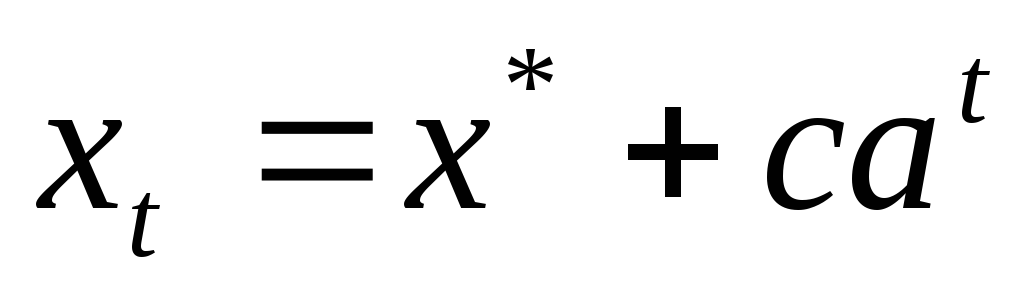
Общий случай – неоднородные, неавтономные системы.

Общая теория линейных систем.
Линейной системой первого порядка называется система, динамика которой задается уравнением:
![]()
![]() вектор
nx1,
эндогенные переменные, вектор состояния
вектор
nx1,
эндогенные переменные, вектор состояния
А – матрица nxn
![]() вектор
nx1,
вектор управления. Экзогенные переменные.
вектор
nx1,
вектор управления. Экзогенные переменные.
Пример:
n = 2
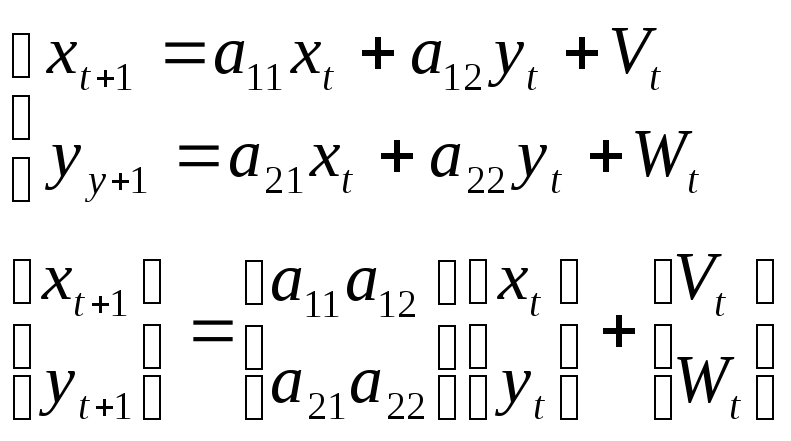
Задача: найти
![]()
Для линейных систем в общем случае имеет место принцип суперпозиции:
Общее решение
системы
![]() (1) = комплиментарная функция (общее
решение однородной системы
(1) = комплиментарная функция (общее
решение однородной системы![]() + любое частное решение системы).
+ любое частное решение системы).![]()
![]()
Линейные однородные системы.
![]() (2)
(2)
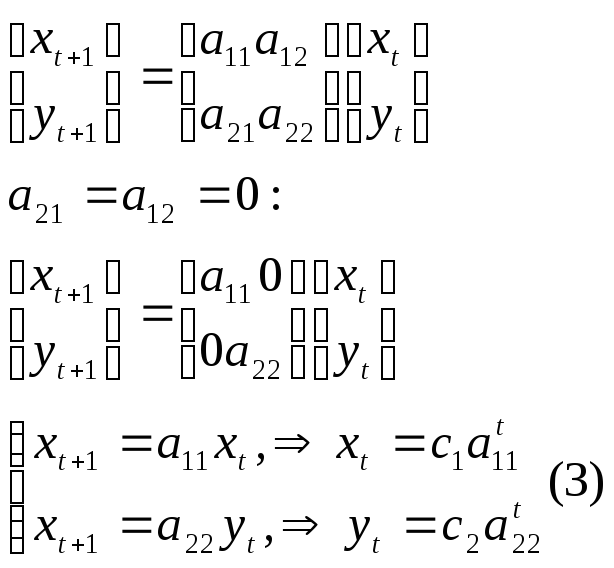
Если матрица А является диагональной. То задача сводится к рассмотренной ранее. С общим решением (3).
Математическая вставка 1.
Комплексные числа.
![]() вещественные
числа
вещественные
числа
а – вещественная часть комплексного числа
b – мнимая часть комплексного числа
![]() сопряженное
комплексному числу с
сопряженное
комплексному числу с
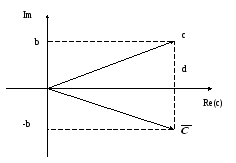

r
– длина вектора с =
![]() норма комплексного числа с
норма комплексного числа с
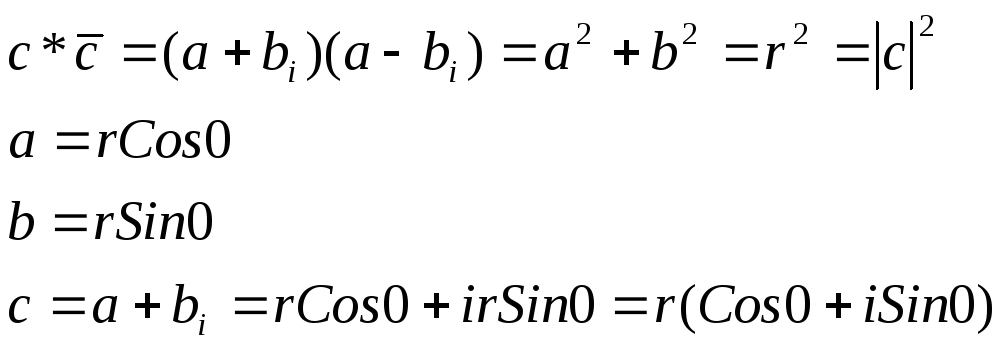
Представление в такой форме называется тригонометрической формой комплексного числа с.
В результате разложения этой формулы в ряд Тейлора получается формула Эйлера:
![]()
Комплексное число с при помощи формулы Эйлера м.б. представлено также в экспоненциальной форме:
![]()
Математическая вставка 2.
Собственные числа и собственные векторы.
Ах = у
![]()


Вектор е называется
собственным вектором матрицы А, если
![]() ,
при этом число
,
при этом число![]() называется собственным числом матрицы
А.
называется собственным числом матрицы
А.
Пример:
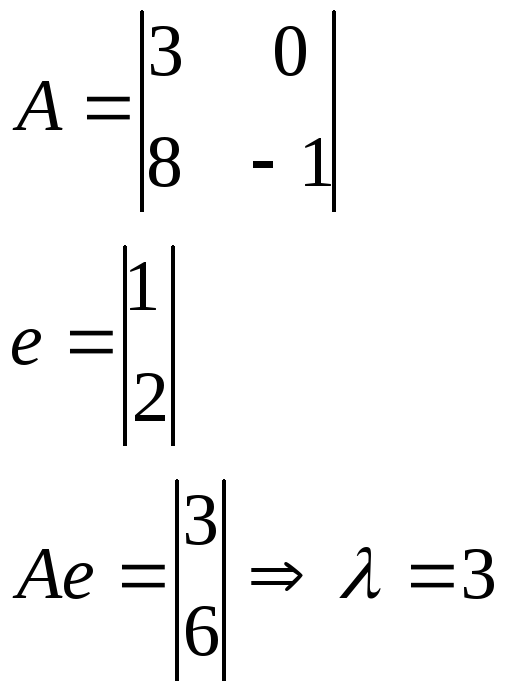
Вектор е является
собственным вектором матрицы А,
соответствующим собственному числу
![]() .
.
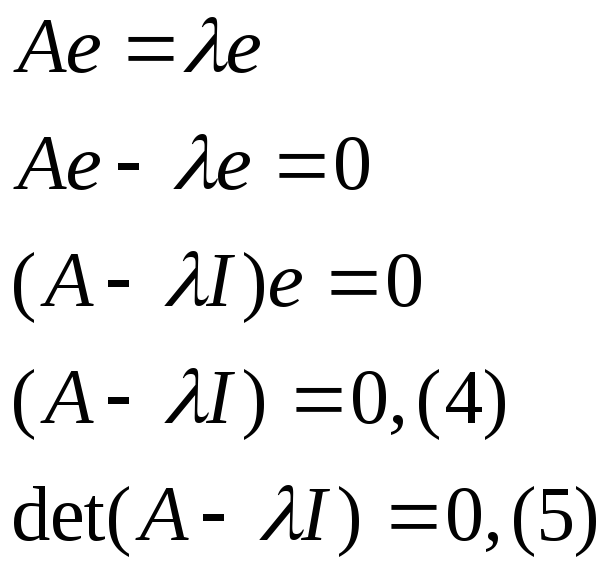
Уравнение (5) – характеристическое уравнение для матрицы А.
Пример:
n = 2
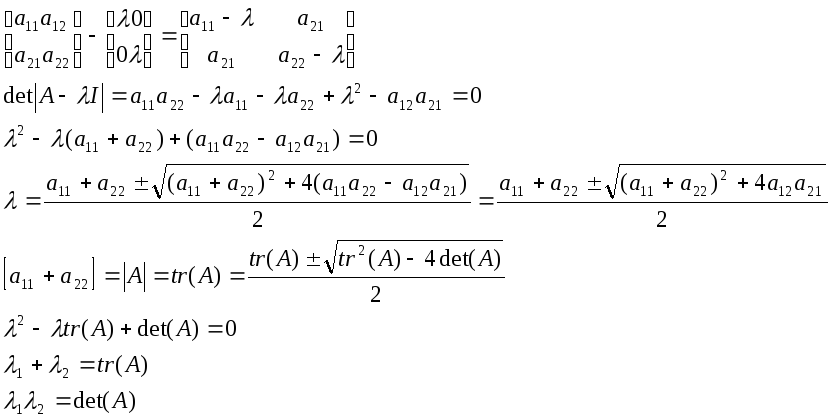
Теорема: сумма собственных чисел матрицы равна следу матрицы, а П равно det.
Теорема: у квадратной матрицы размерностью n м.б. не больше n собственных чисел.
Они м.б. вещественными или комплексными. При этом каждому комплексному собственному числу будет соответствовать другое собственное число, сопряженное к первому.
Пример:
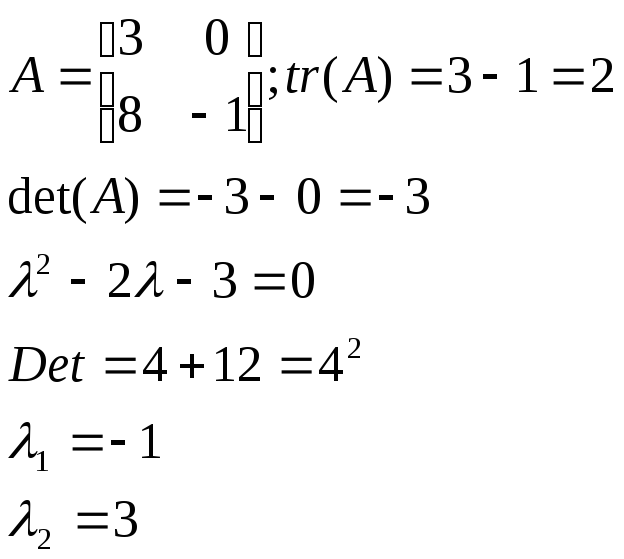
После определения собственных чисел можно определить собственные векторы матрицы А.
Будем искать собственный вектор в форме:

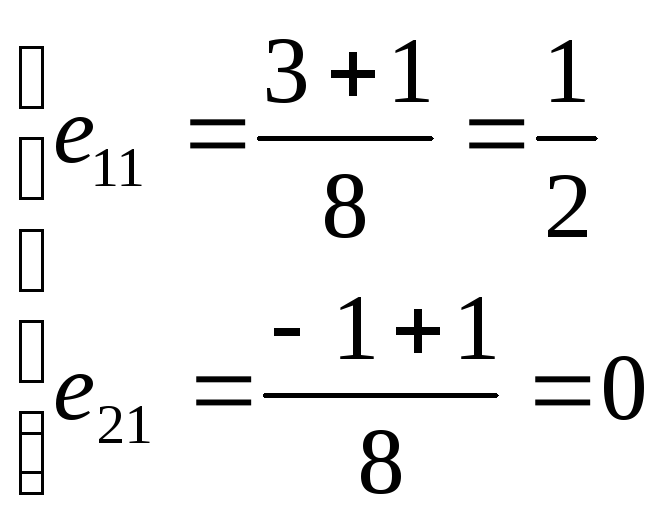
Соответствующие векторы соответствующие различным собственным числам матрицы А являются линейно не зависимыми.
Математическая вставка 3.
Диагонализация матрицы.

Поскольку все собственные векторы являются линейно – независимыми, у матрицы Е должна существовать обратная матрица.
![]()
![]() диагональная
матрица
диагональная
матрица
![]()
Найдем для матрицы
А собственную матрицу Е и матрицу
собственных чисел
![]() .
.
![]()
Для n = 2 (6) имеет вид:

Случай 1:
![]() вещественные
вещественные
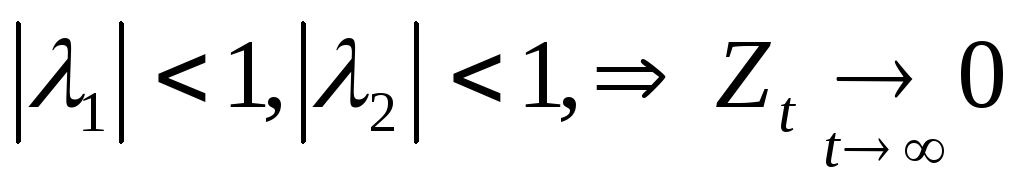
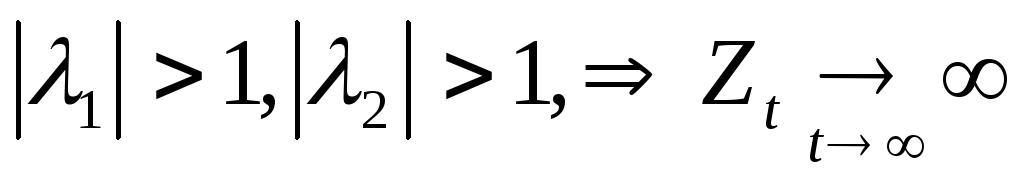
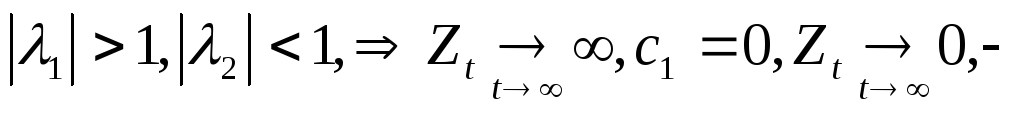 седловое
решение.
седловое
решение.
Случай 2:
![]() комплексные
комплексные
Собственные векторы: если у матрицы А собственные числа собственные, то и собственные векторы, соответствующие этим числам также будут комплексными и сопряженными:
![]()
Из (1) следует, что
![]()
Аналогично:
![]()
Пусть:
![]()
Тогда:
![]()

![]() являются решениями
исходного разностного уравнения
являются решениями
исходного разностного уравнения
![]()
![]()
Поскольку
![]() периодические
функции, то в случае комплексных
собственных чисел общее решение системы
соответствует периодическим колебаниям.
периодические
функции, то в случае комплексных
собственных чисел общее решение системы
соответствует периодическим колебаниям.
Колебания м.б. затухающими или стабильными:
![]() затухающие
затухающие
![]() расходящиеся
расходящиеся
![]() стабильные
стабильные
Неоднородные автономные уравнения.
![]() (2)
(2)
В силу принципа суперпозиции, общее решение системы (2) м.б. представлено в виде:
![]() ,
где
,
где
![]() общее
решение однородной системы
общее
решение однородной системы
![]()
![]() частное
любое решение (2)
частное
любое решение (2)
Пусть
![]()
![]() - неподвижная точка
(2)
- неподвижная точка
(2)
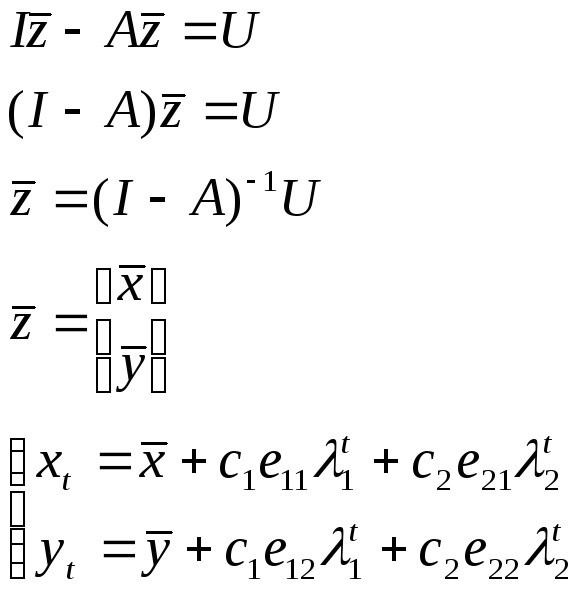
общее решение (2)
рассмотрим случай
седловых решений, когда:
![]()
Седловое решение
соответствует случаям, когда
![]() .
Тогда общее решение:
.
Тогда общее решение:
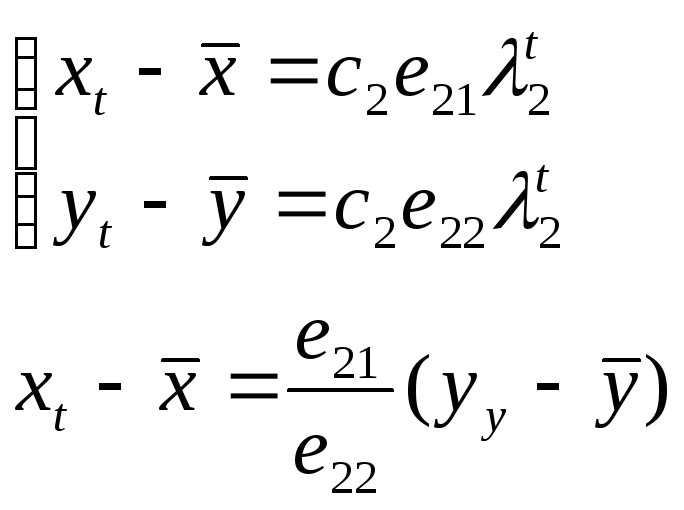
Фазовые диаграммы для двумерных систем.
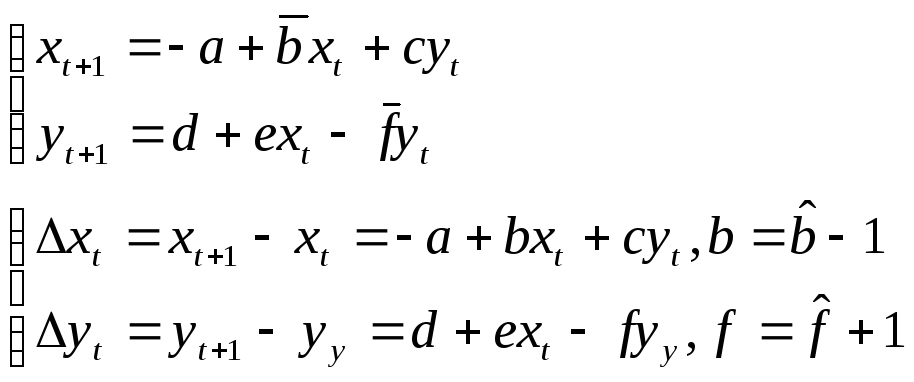
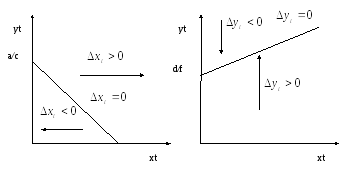

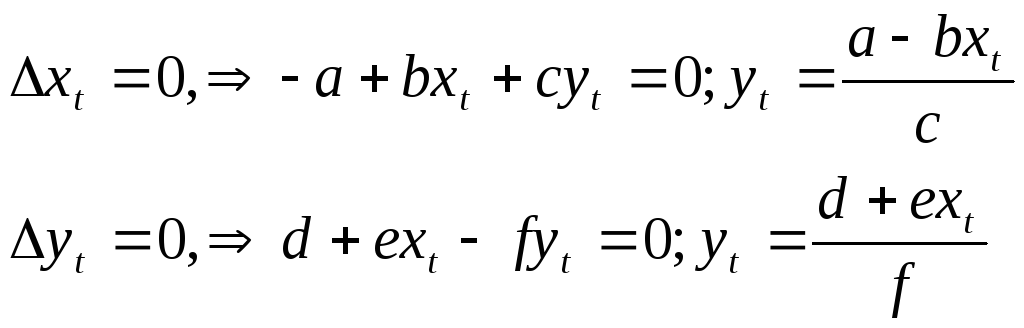
Элементы теории нелинейных систем.
![]()
![]() вектор
состояния n
x
1
вектор
состояния n
x
1
![]() вектор
управления n
x
1
вектор
управления n
x
1
![]() вектор
состояния в прошлом периоде n
x
1
вектор
состояния в прошлом периоде n
x
1


В общем случае нелинейные системы не имеют аналитического решения:
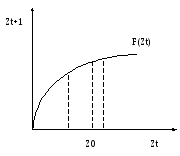

Основным методом решения нелинейных систем является метод линеаризации. Он заключается в том, что область определения функции разбивается на несколько интервалов. В каждом из них нелинейная функция f(Z) апроксимируется линейной функцией касательной к кривой f(Z) в середине интервала.
Пример 1:
Логистическая модель роста.
![]() процентная
ставка
процентная
ставка
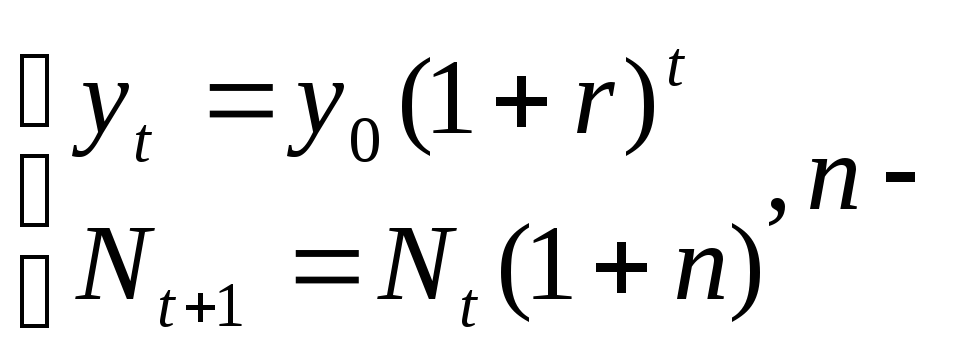 коэффициент
прироста населения
коэффициент
прироста населения
Предположим, что
![]() размер
популяции в моментt
в процентах от максимально – возможного.
размер
популяции в моментt
в процентах от максимально – возможного.
Логистическая
модель:
![]()
![]() коэффициент
пропорциональности, который выполняет
нормирующую функцию.
коэффициент
пропорциональности, который выполняет
нормирующую функцию.
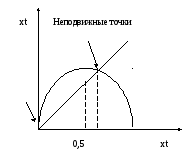

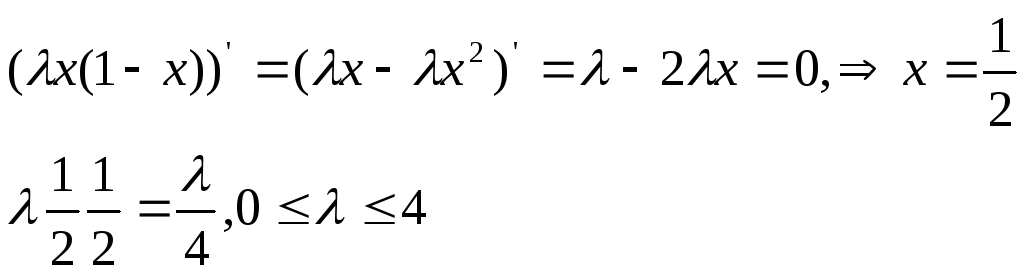
Найдем неподвижные точки:

Построим несколько
фазовых диаграмм, отвечающим различным
значениям
![]() :
:




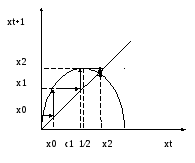

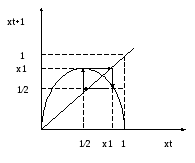

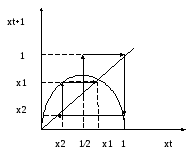

Осциллирующие колебания без определенного периода и определенной амплитуды называются в теории динамических систем хаотическим движением. Для х траекторий характерна большая степень зависимости поведения от начальных условий. Небольшие погрешности в начальном состоянии системы усиливаются с течением времени и через несколько периодов состояние двух систем с почти идентичными начальными условиями будут существенно различаться – «эффект мотылька».
Модель экономического роста Солоу.
Введем обозначения:
![]() размер
капитала в период t
размер
капитала в период t
![]() рабочая
сила в период t
рабочая
сила в период t
![]() инвестиции
в период t
инвестиции
в период t
![]() ВВП
в период t
ВВП
в период t
(1)
![]()
![]() потребление
в период t
потребление
в период t
![]()
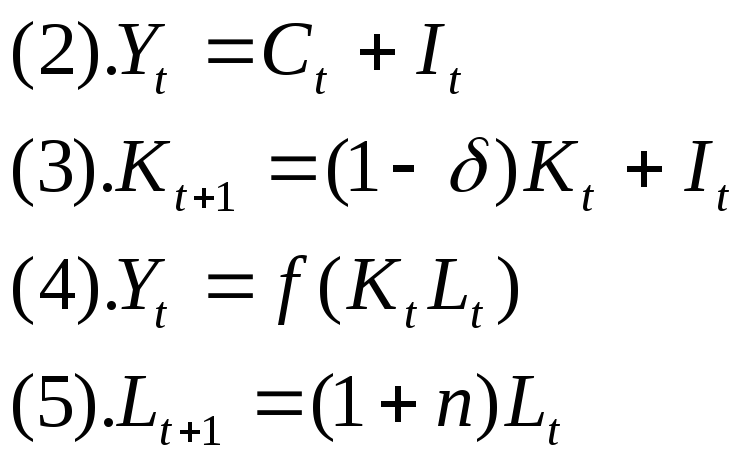
Математическая вставка 4.
Однородные функции.
Функция f(x)
векторного аргумента х называется
однородной порядка n,
если для любого
![]()
Примеры:
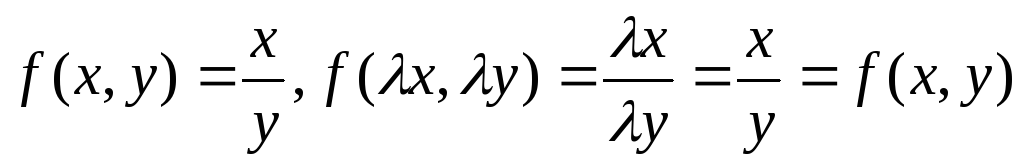 ,
однородная 0го порядка
,
однородная 0го порядка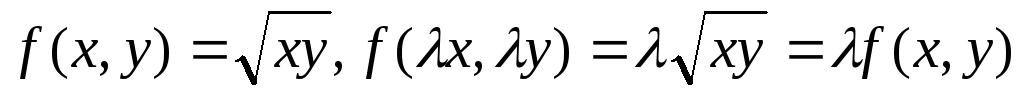 ,
однородная 1го порядка
,
однородная 1го порядка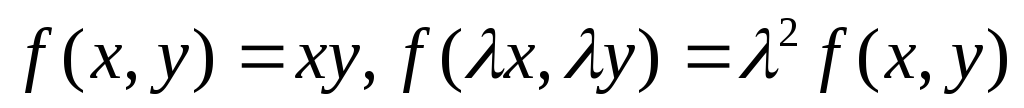 ,
однородная 2го порядка
,
однородная 2го порядка - неоднородная
- неоднородная
![]()
Если
 , то однородная 1го порядка
, то однородная 1го порядка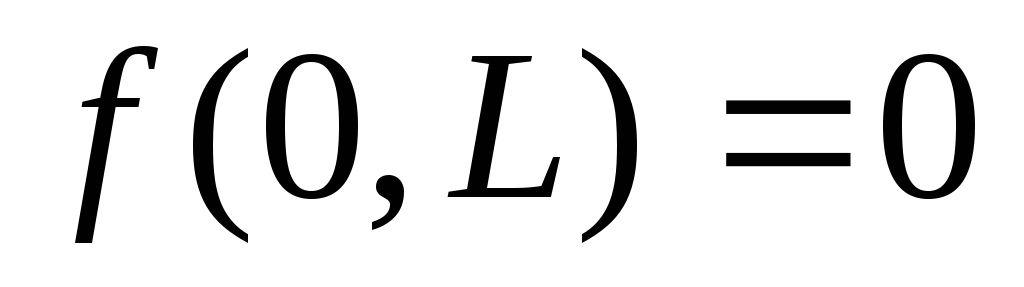
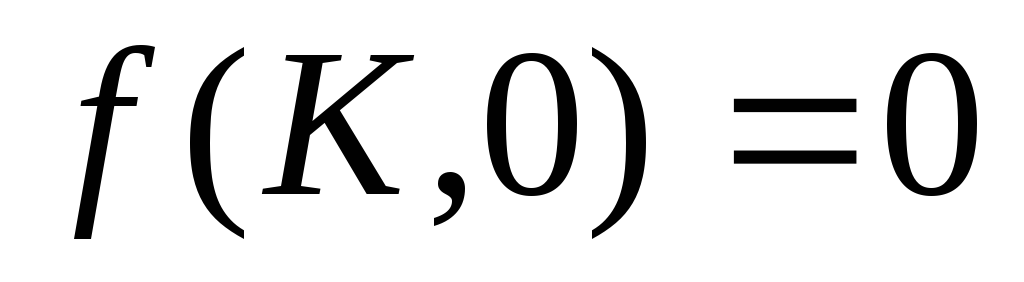
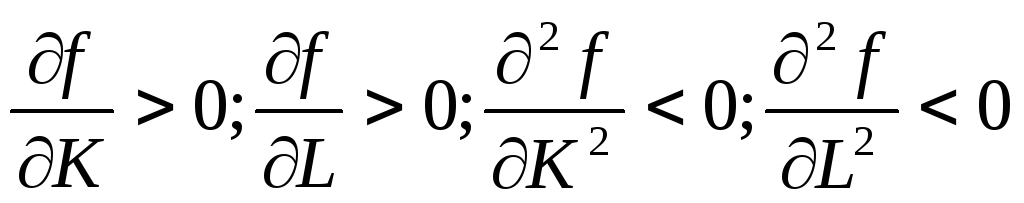
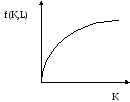

Условия:
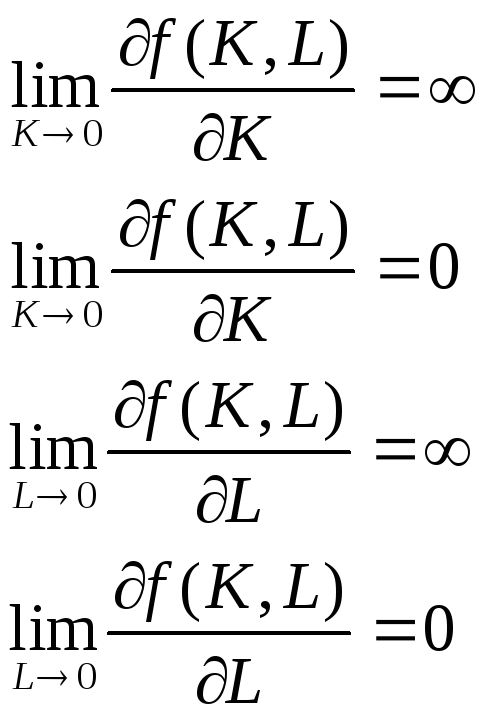
Обозначим прописными буквами переменные в пересчете на душу населения:
![]() ВВП
на душу населения
ВВП
на душу населения
![]()
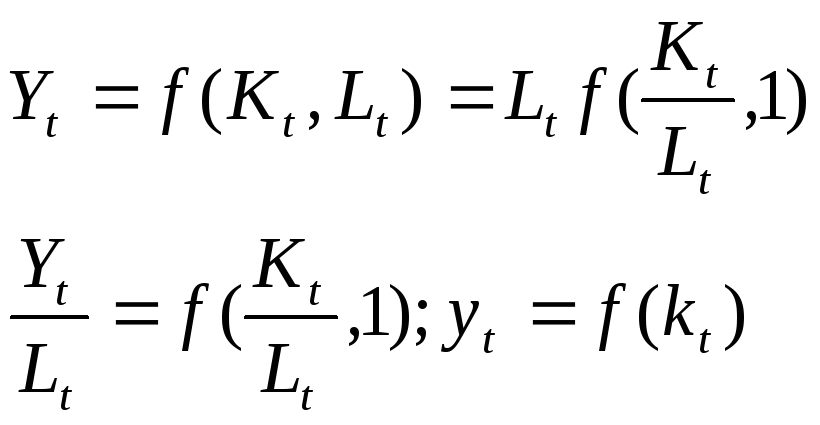
Из (3)

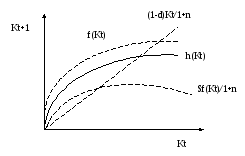

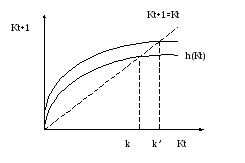

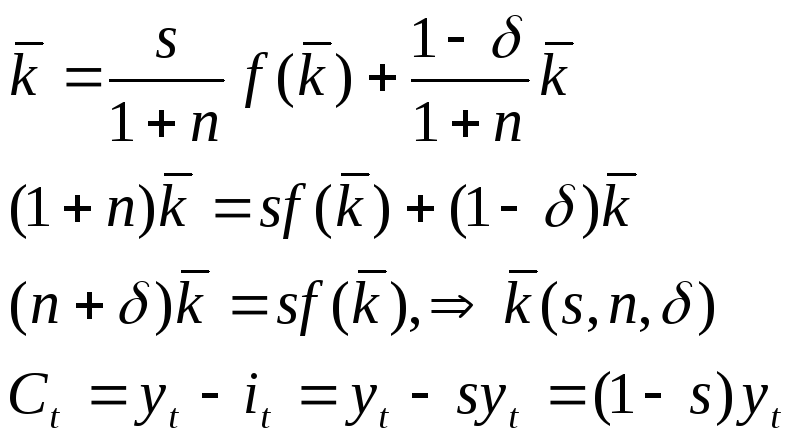
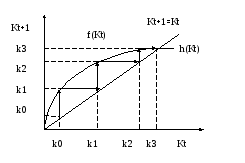

Увеличение нормы сбережений имеет два эффекта:
увеличивает количество капитала в стационарном состоянии, а значит и Vввп на душу населения.
уменьшает долю ВВП, приходящуюся на потребление.
Первый эффект увеличивает потребление на душу населения в стационарном состоянии, а второй – уменьшает.
Возникает вопрос: существует ли оптимальная S, гарантирующая максимум С в стационарном состоянии.
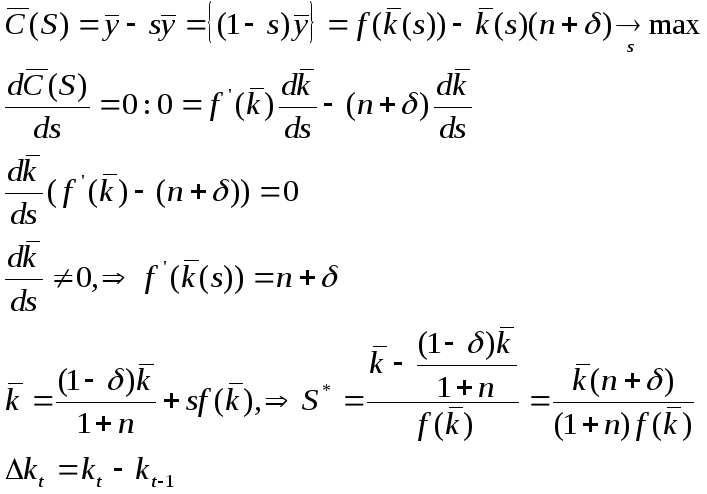
Темп прироста =
![]()

Введение в теорию оптимального управления.
![]()
Задача оптимального
управления состоит в выборе
последовательности управляющих
воздействий
![]() ,
с тем, чтобы достичь определенной цели.
,
с тем, чтобы достичь определенной цели.
![]() прибыль
(критерий оптимальности) в момент t
прибыль
(критерий оптимальности) в момент t

Мы ограничимся рассмотрение задач с фиксированным периодом управления.
Основным принципом при решении подобных задач является метод обратной индукции, заключающийся в поиске оптимального решения от последнего периода к первому.
Пример 1:
(пираты)

Пример 2:
N периодов времени. В каждый из периодов появляется один покупатель.
Каждый покупатель
согласен заплатить за товар СВ
![]() .
.
Если
![]() ,
товар покупается; прибыль продавца = Р.
,
товар покупается; прибыль продавца = Р.
Задача – максимизировать прибыль.
Решение задачи –
последовательность цен
![]() .
.
Обозначим через Vt ожидаемую прибыль продавца в момент t, если до этого товар не был продан.
t = N