
Maloletov-diss
.pdf171
4. Подынтегральная функция качества зависит только от обобщённого ускорения.
Φ=∑ k j f j (q¨ ) |
(3.23) |
j |
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
k f |
¨ ¨ ¨ |
) |
q2+ k f |
¨ ¨ |
) |
q(4)=0 |
(3.24) |
|||
(∑j |
j |
|
(∑j |
j |
|
|||||
|
j ,(q q q) |
|
|
j ,(q q) |
|
|
|
|||
С помощью замены переменной a=q¨ порядок уравнения может быть понижен:
k |
|
f |
a2 |
+ |
k |
|
f |
a=0 |
(3.25) |
(∑j |
j |
|
j ,(a aa ))˙ |
(∑j |
|
j |
|
j ,(a a))¨ |
5. Подынтегральная функция качества зависит только от обобщённой координаты и обобщённого ускорения.
Φ=∑ k j f j (q , q¨ ) |
(3.26) |
j |
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
|
∑ k j f j ,(q)+∑ k j f |
|||||
|
∑ |
j |
|
j |
∑ |
|
+2 |
k |
f |
q q+ |
k |
||
|
j |
|
j ,(q q¨ q¨ ) ˙ |
|
||
|
j |
|
|
|
j |
|
|
|
q2+ |
∑ |
k |
j |
f |
|
j ,(qq q¨ ) ˙ |
|
|
|
||||
|
|
|
|
j |
∑ |
|
|
j |
f |
j ,(q¨ q¨ |
q2+ |
k |
|||
|
q¨ ) |
|
|||||
|
|
|
|
|
|
j |
|
q+ |
|
|
j ,(q q¨ ) ¨ |
(3.27) |
|
j f j ,(q¨ q¨ ) q(4 )=0 |
||
|
172
6. Подынтегральная функция качества зависит только от обобщённой скорости и обобщённого ускорения.
Φ= |
∑ |
k |
j |
f |
(q , q) |
(3.28) |
|
|
|
j ˙ ¨ |
|||
|
j |
|
|
|
|
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
∑ |
k |
j |
f |
j ,(q¨ |
q¨ ) |
q(4 )+ |
∑ |
k |
j |
f |
j ,(q¨ |
q¨ |
q2+ |
∑ |
k |
j |
f |
j ,(q˙ |
q˙ |
q2+ |
||||||
|
|
|
|
|
|
|
q¨ ) |
|
|
|
|
q¨ ) ¨ |
||||||||||||||
j |
|
|
|
+2 |
∑ |
k |
|
f |
j |
|
|
q q− |
∑ |
k |
|
f |
j |
|
|
q=0 |
(3.29) |
|||||
|
|
|
|
j |
j ,(˙q q¨ |
|
j |
j ,(q˙ |
|
|||||||||||||||||
|
|
|
|
|
|
|
q¨ ) ¨ |
|
|
|
q˙ ) ¨ |
|
|
|
||||||||||||
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
С помощью замены переменной v=q˙ порядок уравнения может быть понижен:
∑ |
k |
j |
f |
j ,(v˙ |
v+ |
∑ |
k |
j |
f |
j ,(v˙ |
|
v2+ |
∑ |
k |
j |
f |
v2 |
+ |
|||||||
|
|
v˙ ) |
|
|
|
|
v˙ v˙ ) ¨ |
|
|
|
j ,(v v v˙ ) ˙ |
|
|||||||||||||
j |
|
|
|
|
∑ |
|
|
|
|
j |
|
|
|
|
|
∑ |
|
|
j |
|
|
|
|
(3.30) |
|
|
|
|
+2 |
k |
j |
f |
j ,(v v˙ |
|
v v− |
k |
j |
f |
|
|
|
v=0 |
|||||||||
|
|
|
|
|
|
|
v˙ ) ˙ ¨ |
|
|
|
j ,(v v) ˙ |
|
|||||||||||||
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
7. Подынтегральная функция качества не зависит от времени.
Φ= |
∑ |
k |
j |
f |
j |
(q , q , q) |
(3.31) |
|
|
|
˙ ¨ |
||||
|
j |
|
|
|
|
|
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
173 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∑ |
k |
j |
f |
j ,(q¨ |
q¨ ) |
q(4 )+ |
∑ |
k |
j |
f |
|
|
|
|
q2+ |
∑ |
k |
|
j |
f |
|
|
q2+ |
∑ |
k |
j |
f |
j , (q˙ |
|
q2+ |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
j ,(q¨ q¨ q¨ ) |
|
|
|
|
|
|
j ,(qq q¨ ) ˙ |
|
|
|
q˙ q¨ ) ¨ |
|
|||||||||||||||||||||||||
j |
|
|
|
∑ |
|
|
|
|
|
j |
|
|
|
|
|
|
|
∑ |
|
|
|
|
j |
|
|
|
|
|
|
|
|
∑ |
|
|
|
j |
|
|
|
|
|
|
|
|||
|
|
+2 |
k |
j |
f |
j ,(q q˙ q¨ ) |
q q+2 |
k |
j |
f |
j ,(q q¨ |
|
|
q q+2 |
k |
j |
f |
j ,(q˙ |
|
q q+ |
(3.32) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
˙ ¨ |
|
|
|
|
|
|
q¨ ) |
˙ |
|
|
|
|
|
q¨ q¨) ¨ |
|
||||||||||||||||||||||||
|
|
|
∑ |
j |
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
j |
|
|
|
|
|
∑ |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
+ |
k |
j |
|
f |
|
|
|
q− |
k |
j |
f |
j ,(q q˙ ) |
q− |
k |
j |
f |
|
q+ k |
j |
f |
j ,(q) |
=0 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
j ,(q q¨ ) ¨ |
|
|
|
|
˙ |
|
|
|
|
|
j ,(˙q q˙ ) ¨ |
|
|
∑ |
|
|
|
|
|||||||||||||||||||||
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
8. Подынтегральная функция качества зависит только от времени и обобщённой координаты.
Φ=∑ k j f j (t ,q) |
(3.33) |
j |
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
∑ k j f j ,(q )(t ,q)=0 |
(3.34) |
j |
|
Уравнение (3.34) не является дифференциальным, задаёт зависимость обобщённой координаты от времени, которая в общем случае не удовлетворяет граничным условиям. Другими словами, экстремум функционала (3.33) может достигаться лишь в тех частных случаях, когда кривая (3.34) проходит через граничные точки.
9. Подынтегральная функция качества зависит от обобщённой скорости линейно и не зависит от производных более высокого порядка.
∑ |
∑ |
|
∑ |
) |
(3.35) |
j |
j |
( j |
|
||
Φ= |
k j (a j (t ,q)+b j (t ,q)q˙ )= |
k j a j (t ,q)+ |
|
k j b j (t ,q) q˙ |
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:

174
∑ k j (a j ,(q)(t ,q)−b j ,(t )(t ,q))=0 |
(3.36) |
j |
|
Так же как и в предыдущем случае, уравнение (3.36) является конечным, то есть, вариационная задача обычно не имеет решения в классе непрерывных функций.
10. Подынтегральная функция качества зависит от обобщённой скорости и времени.
Φ=∑ k j f j (t , q˙ )
j
Уравнение Эйлера-Лагранжа:
∑ |
|
|
|
˙ |
∑ |
|
|
|
˙ ˙ |
) |
|
j |
k |
j |
f |
+ |
( j |
k |
j |
f |
j ,(q q) |
q=0 |
|
|
|
|
j ,(t q ) |
|
|
|
|
¨ |
удобнее представить в виде
dt (∑k j f j ,(q˙ ))=0
d
j
откуда следует дифференциальное уравнение первого порядка
(3.37)
(3.38)
(3.39)
∑ k j f j ,(q˙ )=С1 . |
(3.40) |
j |
|
11. Подынтегральная функция качества не зависит от обобщённого ускорения или более старших производных.
175
Φ= |
∑ |
k |
j |
f |
j |
(t ,q , q) |
(3.41) |
|
|
|
˙ |
||||
|
j |
|
|
|
|
|
|
Уравнение Эйлера-Лагранжа:
∑ |
k |
j ( |
f |
j ,(q) |
− f |
j ,(t , q) |
− f |
q− f |
q =0 |
(3.42) |
|
|
|
|
j ,(q q˙ ) ˙ |
j ,(q˙ q˙) ¨ ) |
|||||
j |
|
|
|
|
|
|
|
|
|
|
12. Подынтегральная функция качества зависит от времени, обобщённой координаты и линейно зависит от обобщённого ускорения.
∑ |
|
|
|
|
|
∑ |
|
|
|
∑ |
|
|
) |
|
(3.43) |
j |
k |
j ( |
a |
(t ,q)+b |
(t ,q)q = |
j |
k |
a |
( j |
k |
b |
|
|
||
Φ= |
|
(t ,q)+ |
|
(t ,q) q |
|
||||||||||
|
|
j |
j |
¨ ) |
|
j |
j |
|
|
j |
j |
|
¨ |
|
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
j |
|
|
|
|
|
|
|
( j |
|
|
) |
|
( j |
|
|
) |
q2+2 |
( j |
|
|
) |
|
|
|
∑ |
k |
j ( |
a |
j ,(q) |
+b |
j ,(t t)) |
+2 |
∑ |
k |
b |
j ,(t q) |
q+ |
∑ |
k |
b |
|
∑ |
k |
b |
|
q=0 |
(3.44) |
||
|
|
|
|
j |
|
˙ |
|
j |
|
j ,(qq) ˙ |
j |
|
j ,(q) ¨ |
|||||||||||
13. Подынтегральная функция качества зависит только от времени и обобщённого ускорения.
Φ= |
∑ |
k |
j |
f |
j |
(t , q) |
(3.45) |
|
|
|
¨ |
||||
|
j |
|
|
|
|
|
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
j |
|
|
|
( |
j |
|
|
) |
|
( |
j |
|
|
) |
|
( |
j |
|
|
) |
q(4)=0 |
|
∑ |
k f |
¨ |
+2 |
|
∑ |
k f |
¨ ¨ |
|
q+ |
∑ |
k f |
¨ ¨ ¨ |
|
q2+ |
∑ |
k f |
¨ ¨ |
|
(3.46) |
|||
|
j |
j ,(t t q ) |
|
|
j |
j ,(t q q) |
|
|
|
|
j |
j ,(q q q ) |
|
|
|
|
j |
j ,(q q) |
|
|
|
|
176
Так же как и в случае 4, это уравнение является дифференциальным уравнением второго порядка относительно обобщённого ускорения a=q¨ :
∑ |
|
|
|
|
|
∑ |
|
|
|
|
) |
|
∑ |
|
|
|
|
) |
|
∑ |
|
|
|
) |
|
(3.47) |
j |
k |
|
f |
|
+2 |
( j |
k |
|
f |
|
|
( j |
k |
|
f |
|
|
( j |
k |
|
f |
a=0 |
|
|||
|
|
j |
|
j ,(t t a ) |
|
|
|
j |
|
j ,(t a a) |
|
˙ |
|
|
j |
|
j ,(aa a) |
|
˙ |
|
|
j |
|
j ,(aa ) ¨ |
|
|
14. Подынтегральная функция качества зависит от времени, обобщённой координаты и обобщённого ускорения.
Φ=∑ k j f j (t ,q , q¨ ) |
(3.48) |
j |
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:
|
∑ |
k |
j |
f |
|
+ |
∑ |
k |
j |
f |
|
|
|
|
q2+ |
∑ |
k |
j |
f |
j , (q¨ q¨ |
q2+ |
|
|||||||||||
|
|
|
|
j ,(q ) |
|
|
|
|
j ,(qq q¨ ) ˙ |
|
|
|
|
|
q¨ ) |
|
|||||||||||||||||
|
j |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
+2 |
∑ |
k |
j |
f |
|
|
|
q+2 |
∑ |
k |
j |
f |
j ,(t q¨ |
|
q+2 |
∑ |
k |
j |
f |
q q+ |
(3.49) |
||||||||||||
|
|
|
|
|
j ,(t q q¨ ) ˙ |
|
|
|
|
|
q¨ ) |
|
|
|
|
j ,(q q¨ q¨ ) ˙ |
|||||||||||||||||
|
j |
|
|
|
|
|
|
∑ |
|
|
|
|
|
j |
|
|
|
|
∑ |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
k |
j |
f |
|
|
|
|
q+ |
k |
j |
f |
j ,(q¨ q¨ ) |
q(4)=0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
j ,(q q¨ ) ¨ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
15. Подынтегральная функция качества зависит от времени, обобщённой скорости и обобщённого ускорения.
Φ=∑ k j f j (t , q˙ , q¨ ) |
(3.50) |
j |
|
Уравнение Эйлера-Лагранжа в этом случае имеет вид:

177
∑ |
k |
j |
f |
j ,(q¨ |
q¨ ) |
q(4 )+ |
∑ |
k |
j |
f |
|
j ,(t t q¨ ) |
+ |
∑ |
k |
j |
f |
|
|
q2+ |
∑ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j ,(q¨ q¨ q¨ ) |
|
|||||||||||||||||||
j |
|
|
|
|
∑ |
|
|
|
|
j |
|
|
|
|
|
|
∑ |
|
|
|
j |
|
|
|
|
|
|
∑ |
|
|
j |
||
|
|
+2 |
k |
j |
f |
|
|
|
q+2 |
k |
j |
f |
j ,(t q¨ |
|
q+2 |
k |
j |
f |
|||||||||||||||
|
|
|
|
|
|
|
j ,(t q˙ q¨ ) ¨ |
|
|
|
|
|
|
|
q¨ ) |
|
|
|
|||||||||||||||
|
|
|
|
|
j |
|
|
|
|
|
|
∑ |
|
|
|
|
j |
|
|
|
|
∑ |
|
|
|
|
j |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
− |
k |
j |
f |
j ,(t q˙ ) |
− |
k |
j |
f |
|
q=0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j ,(q˙ q˙ ) ¨ |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
k |
j |
f |
j ,(q˙ q˙ |
q2+ |
|
|
|
q¨) |
¨ |
||
|
|
|
q q+ |
(3.51) |
|
j ,(˙q q¨ q¨ ) ¨ |
|
||||
С помощью замены переменной v=q˙ порядок уравнения может быть понижен:
∑ |
k |
j |
f |
j ,(v˙ |
v+ |
∑ |
k |
j |
f |
j ,(t t v˙ ) |
+ |
∑ |
k |
j |
f |
|
j ,(v˙ v˙ v˙ ) |
v2+ |
∑ |
k |
j |
f |
v2+ |
|
||||||||||||
|
|
v˙ ) |
|
|
|
|
|
|
|
|
¨ |
|
|
|
j ,(v v v˙ ) ˙ |
|
||||||||||||||||||||
j |
|
|
|
∑ |
|
|
|
j |
|
|
|
|
|
∑ |
|
|
|
j |
|
|
|
|
|
|
|
∑ |
|
|
j |
|
|
|
|
|
|
|
|
+2 |
k |
j |
f |
|
|
v+2 |
k |
j |
f |
|
|
|
|
v+2 |
k |
j |
f |
j ,(v v˙ |
v v+ |
(3.52) |
|||||||||||||||
|
|
|
|
|
|
j ,(t v v˙ ) ˙ |
|
|
|
|
|
|
|
j ,(t v˙ v˙ ) ¨ |
|
|
|
|
v˙) ˙ ¨ |
|||||||||||||||||
|
|
|
|
j |
|
|
|
|
∑ |
|
|
|
j |
|
|
|
|
|
∑ |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
− |
k |
j |
f |
j ,(t v) |
− |
k |
j |
f |
|
v=0 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j ,(v v) ˙ |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.1.1.Оптимизация закона управления линейным приводом
Описанный подход применён при оптимизация работы линейного привода фирмы «Exlar» (рисунок 3.1) использованного в приводах движителей шагающей машины «Ортоног».
а) |
б) 1 |
2 |
|
|
|
А |
Q В |
|
|
3 |
L |
|
|
|
Рисунок 3.1 –– Линейный привод фирмы «Exlar»: а) внешний вид, б) расчётная схема. 1 — двигатель, 2 — редуктор, 3 — шток.
Рассматривается перемещение штока из положения А в положение В. На границах участка AB скорость штока задаётся равной нулю. В качестве

178
обобщенной координаты выбирается угол поворота вала двигателя φ. Заданному перемещению штока за время τ на величину L соответствует поворот вала двигателя на угол φτ. Затем осуществляется движение в обратную сторону по тому же закону. Поэтому τ – время половины цикла. Приведённый к валу двигателя постоянный момент инерции обозначается через J. Полезная сила сопротивления движению Q задается пропорциональной угловой скорости φ˙ , коэффициент пропорциональности обозначается через μ. Оптимизация осуществляется по обобщённому критерию (2.13) с подынтегральной функцией качества Φ:
|
|
|
|
|
|
|
|
k |
1 |
2 |
|
2 |
|
kW τ α |
|
2 |
|
Φ=k |
|
f |
+k |
|
f |
|
= |
|
|
r |
φ |
+ |
|
( J φ+μφ) |
(3.53) |
||
1 |
W |
W |
|
2 |
̄ |
||||||||||||
|
1 |
|
|
|
g |
|
¨ |
|
|
¨ ˙ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
где f 1 — функция, соответствующая частному критерию комфортабельности движения (минимума среднеквадратичного ускорения штока); f W — функция, соответствующая частному критерию минимума тепловых потерь в электродвигателе постоянного тока; k1, kW — весовые коэффициенты; r — условный радиус, связывающий между собой перемещение штока и угол поворота вала двигателя; α — постоянный коэффициент, характеризующий двигатель; g, A
— постоянные нормирующие коэффициенты, имеющие размерность ускорения и работы соответственно.
Выражение (3.53) соответствует частному случаю (3.28), а уравнение ЭйлераЛагранжа (3.29) приобретает вид
( |
k1 |
2 |
|
2 kW τ α |
)φ |
(4) |
−(μ |
2 kW τ α |
)φ¨ =0 . |
|
||
|
r |
+J |
|
|
|
|
|
(3.54) |
||||
g2 |
Ā |
|
Ā |
|||||||||
Граничные условия:
179
φ˙ 0=φ˙ τ =ω0
φ0=0 . (3.55) φτ=2 π
Оценка осуществляется по частным критериям: H1 — квадрату среднеквадратичного ускорения и HW — квадрату среднеквадратичного значения момента сил, развиваемого двигателем:
̃ |
|
1 |
τ |
|
|
2 |
d t |
|
|||
H 1= |
τ |
∫φ¨ |
|
|
|||||||
|
|
τ |
0 |
|
|
|
2 |
(3.56) |
|||
|
1 |
|
|
J |
|
|
2 |
|
|||
̃ |
|
|
|
|
|
|
|||||
H W = |
τ |
∫0 |
(μ |
φ¨ |
|
+φ˙ ) d t |
|
||||
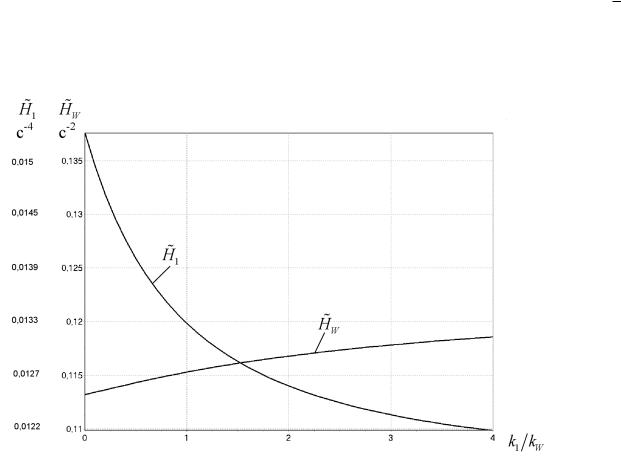
Тогда, при соответствующем выборе нормирующих коэффициентов g и A, можно получить зависимости частных показателей от соотношения весовых коэффициентов, представленные на рисунке 3.2.
Рисунок 3.2 — Зависимости частных показателей качества от соотношения весовых коэффициентов.
180
Их анализ позволяет осуществить субъективный выбор программного режима движения управляемого двигателя.
Решения, получающиеся с помощью уравнения Эйлера-Лагранжа, являются Парето оптимальными, и обычно их принято изображать в виде границы Парето в
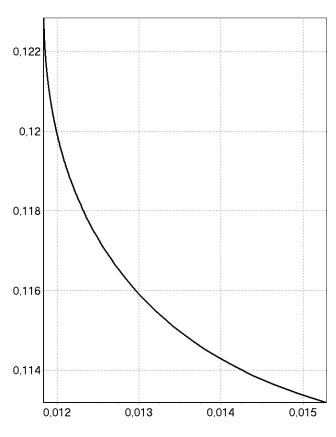
координатных осях H1 и HW (рисунок 3.3).
HW
H1
Рисунок 3.3 — Граница Парето
Однако форма представления, приведённая на рисунке 3.2 в ряде случаев более удобна, так как предоставляет инструмент выбора не только одного из решений, но и весовых коэффициентов, которые позволяют найти это решение. Например, наилучшее (в данном случае — минимальное) значение показателя HW и одновременно наихудшее значение показателя H1 соответствует значению k1 = 0. Стремясь улучшить показатель H1, придётся согласиться на ухудшение показателя HW, и по графикам 3.2 можно определить не только значения самих показателей, но и значения (точнее соотношение) весовых коэффициентов, которые при
