
Индивидуальное задание
.doc|
7.6 |
Линейный сплайн |
Найти экстремумы функции |
Данные к задаче:
|
x |
-3 |
-2.55 |
-2.1 |
-1.65 |
-1.2 |
-0.75 |
-0.3 |
0.15 |
0.6 |
1.05 |
1.5 |
1.95 |
2.4 |
|
y |
0.262 |
-1.032 |
-1.747 |
-1.981 |
-0.564 |
0.774 |
2.400 |
2.131 |
2.2 |
-0.393 |
-1.815 |
-0.788 |
8.030 |
Теория:
Естественная потребность в наличии аппроксимирующих функций, которые сочетали бы в себе локальную простоту многочлена невысокой степени и глобальную на всём отрезке [a,b] гладкость, привела к появлению в 1946 г. так называемых сплайн-функций или сплайнов – специальным образом построенных гладких кусочно-многочленных функций. Получив в 60-х годах XX в. распространение как средство интерполяции сложных кривых, сплайны к настоящему времени стали важной составной частью самых различных вычислительных методов, и нашли широчайшее применение в решении разнообразных научно-технических и инженерных задач.
Пусть отрезок [a,b] разбит точками a=x <x <…<x = b на n частичных отрезков . Сплайном степени m называется функция S (x), обладающая следующими свойствами:
-
функция S (x) непрерывна на отрезке [a,b] вместе со всеми своими производными S (x), S (x), …, S (x) до некоторого порядка p;
-
на каждом частичном отрезке [x ,x ] функция S (x) совпадает с некоторым алгебраическим многочленом P (x) степени m.
Разность m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a,b] производной называется дефектом сплайна.
Простейший пример сплайна даёт непрерывная кусочно-линейная функция, являющаяся сплайном первой степени (линейным сплайном) с дефектом, равным 1. На отрезке [a,b] сама функция S (x) совпадает с некоторым многочленом первой степени.
Линейный сплайн дефекта 1:
P =
P =
S (x) = …
P =
Определение. Пусть функция
![]() определена в некоторой окрестности
определена в некоторой окрестности
![]() ,
,
![]() ,
некоторой точки
,
некоторой точки
![]() своей области определения. Точка
своей области определения. Точка
![]() называется точкой локального максимума,
если в некоторой такой окрестности
называется точкой локального максимума,
если в некоторой такой окрестности
![]() выполняется неравенство
выполняется неравенство
![]() (
(![]() ),
и точкой локального минимума,
если
),
и точкой локального минимума,
если
![]()
![]() .
.
Понятия локальный максимум и локальный минимум объединяются термином локальный экстремум.
Следующая теорема даёт необходимое
условие того, чтобы точка
![]() была точкой локального экстремума
функции
была точкой локального экстремума
функции
![]() .
.
Теорема. Если точка
![]() - это точка локального экстремума функции
- это точка локального экстремума функции
![]() ,
и существует производная в этой точке
,
и существует производная в этой точке
![]() ,
то
,
то
![]() .
.
(доказательство этой теоремы сразу же следует из теоремы Ферма)
Утверждение теоремы можно переформулировать так:
если функция
![]() имеет локальный экстремум в точке
имеет локальный экстремум в точке
![]() ,
то либо
,
то либо
1)
![]() ,
либо
,
либо
2) производная
![]() не существует.
не существует.
Первое достаточное условие. Пусть xо - критическая точка. Если f ¢ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет производную
f ¢ (x) в окрестности точки xо и вторую
производную
![]() в самой точке xо. Если f ¢(xо) = 0,
в самой точке xо. Если f ¢(xо) = 0,
![]() >0 (<0), то точка xо является точкой
локального минимума (максимума) функции
f(x). Если же
>0 (<0), то точка xо является точкой
локального минимума (максимума) функции
f(x). Если же
![]() =0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
Решение:
Вводим исходные данные:
![]()
![]()
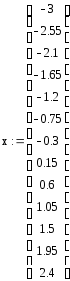
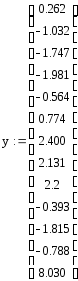
Задаём линейный сплайн:
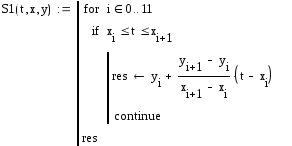
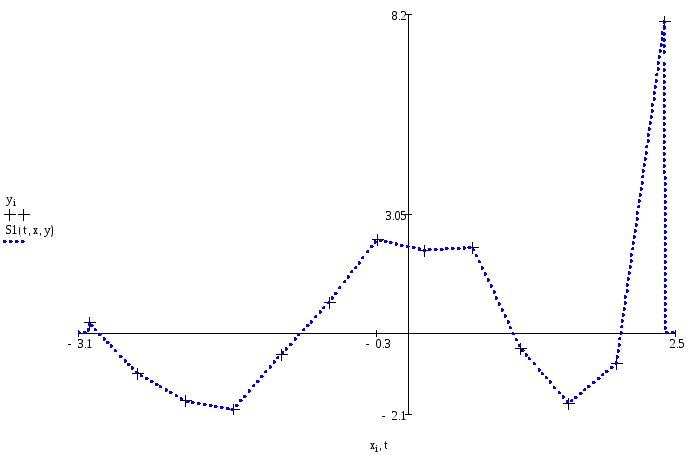
Сплайн имеет вид:
Производные сплайна имеют вид:
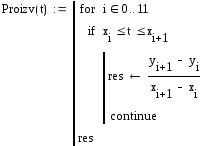
Значения в каждом i-ом x:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
