Среднее Заочное отделение / 4 семестр / Цифровые и микропроцессорные устройства / Программа, методические указания и контрольные задания (ЦиМПУ)

A5F.C83(16) = 10 ∙ 162 + 5 ∙ 161 + 15 ∙ 160 + 12 ∙ 16–1 + 8 ∙ 16–2 + 3 ∙ 16–3 = = 2655.7819824(10).

11011.011(2) = 1 ∙ 24 + 1 ∙ 23 + 0 ∙ 22 + 1 ∙ 21 + 1 ∙ 20 + 0 ∙ 2–1 + 1 ∙ 2–2 + + 1 ∙ 2–3 = 27.375(10).

Правила и примеры перевода чисел в двоичную систему счисления из шестнадцатеричной приведены в [1, с. 6, 7].

Рассмотрим пример:

Переводить десятичные числа в двоичную систему счисления можно различными способами. Наиболее простым является следующий расчетный метод:

Целую часть числа последовательно делят на два до тех пор, по-

ка целая часть частного от последовательного деления станет равна 0. Результат перевода состоит из цифр остатков, причем последний остаток будет представлять старший разряд в записи целой части двоичного числа.

Дробную часть переводят путем последовательного умножения

на два. Результат перевода дробной части получают из цифр целых частей частичных произведений, причем старшим разрядом является первая целая часть.

Целая часть числа переводится точно, дробная – приблизи-

тельно. Точность перевода дробной части зависит от числа знаков после точки (см. [1, c. 8–10]).

Рассмотрим пример перевода десятичного числа 283.64 в двоичную систему счисления с точностью до семи знаков после точки.

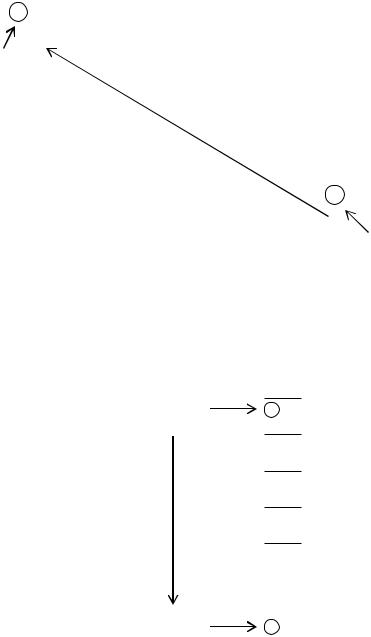
Переведем целую часть числа:

11

Старший

разряд

Переведем дробную часть числа, умножая последовательно на два только дробь, стоящую справа от точки.

0.64

× 2

Старший разряд × 1 .28

2

0.56

× 2

1.12

× 2

Направление чтения × 0.24

2

Запишем результат перевода дробной части: 0.64(10) = 0.1010001(2).

Полный результат перевода: 283.64(10) = 100011011.1010001(2)

Правила представления и суммирования двоичных чисел со знаком в дополнительном коде приведены в [1, с. 14…20]. Перед решением пункта 3 задачи 1 изучите теоретический материал и примеры, приведенные в данных методических указаниях.

Дополнительный код положительного двоичного числа совпадает с его прямым кодом. Дополнительным кодом отрицательного двоичного числа называется его дополнение до граничного числа Xгр. Получается по следующему правилу: в знаковом разряде записывается единица, а во всех других разрядах цифры заменяются на взаимно обратные, после чего к младшему разряду числа добавляется единица.

Аналитически дополнительный код для двоичных чисел, меньше единицы, образуется по формуле:

где Xгр – граничное число,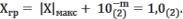

Пример 1.1

Представим в дополнительном коде двоичные числа X1 и X2:

Обратное преобразование, т. е. получение двоичного числа в естественной форме из дополнительного кода выполняется по тому же правилу, что и получение дополнительного кода. Для этого следует вначале заменить все цифры, на взаимно обратные, после чего добавить единицу к младшему разряду. В результате получается прямой код, затем выполняется обратное преобразование из прямого кода к естественной форме числа.

Пример 1.2

Выполним обратное преобразование из дополнительного кода в естественную форму двоичного числа:

13

Полученный результат преобразования совпадает с исходным значением числа X2 в примере 1.1.

При алгебраическом сложении двоичных чисел со знаком в дополнительном коде используются следующие правила:

а) знаковые разряды суммируются так же, как и значащие разряды числа;

б) единица переноса из знакового разряда при сложении в дополнительном коде отбрасывается;

в)если в знаковом разряде суммы получился нуль, то сумма положительна и для перехода к естественной форме числа обратное преобразование не требуется. Если же в знаковом разряде суммы получилась единица, то сумма отрицательна и требуется обратное преобразование.

Рассмотрим примеры.

Пример 1.3

Выполним суммирование двух двоичных чисел X1 = + 0.11001 и X2 = – 0.01011 в дополнительном коде.

14

Результат получился положительным, и обратное преобразо-

полнительном коде. Результат получится отрицательным, и потребуется обратное преобразование.

1 1 1 1 – Переносы

При сложении чисел одного знака может произойти переполнение разрядной сетки, что приведет к искажению результата. На практике для выявления переполнения разрядной сетки применяют модифицированные машинные коды, в которых два знаковых разряда. Для положительных чисел в знаковых разрядах записывается 00, для отрицательных – 11. Появление комбинаций 01 или 10 в знаковых разрядах свидетельствует о переполнении разрядной сетки, т. е. является сигналом ошибки. Например, двоичное число X = – 0.1101 в модифицированном дополнительном коде будет записано следующим образом:

[X]мдоп = 11,0011.

Пример 1.5

Выполним суммирование двух десятичных чисел X1 = + 0.450 и X2 = – 0.575 в двоичной СС с точностью до пяти знаков после запятой

в дополнительном модифицированном коде и сравним результаты суммирования в двоичной и десятичной СС.

Так как | X2 | > | X1 |, то в естественной форме следует выполнить вычитание числа X1 из числа X2 и результату присвоить знак минус.

15

Результаты суммирования в естественной форме и дополнительном модифицированном коде совпадают.

Правило и пример перевода десятичного числа в двоично-

десятичный код 8421 приведены в [1, с. 6]. Рассмотрим пример:

Правила и примеры суммирования десятичных чисел со зна-

ком в коде 8421 приведены в [1, с. 22–27].

Способ суммирования двоично-десятичных чисел зависит от того, какой двоичный код выбран для представления десятичных цифр. Рассмотрим операцию суммирования при использовании кода 8421.

При сложении двоично-десятичных чисел в коде 8421 выполняются дополнительные действия:

–анализ межтетрадных переносов при сложении;

–анализ диапазона двоичных чисел в каждой тетраде начальной суммы;

16

– введение поправок (коррекции) в некоторые тетрады по результатам анализа.

Для упрощения коррекции результата этот процесс обычно делают двушаговым. В результате получается следующее правило сложе-

ния десятичных чисел с одинаковыми знаками в коде 8421:

1) к каждой тетраде любого из операндов прибавить поправку

∆1 = 6(10) = 0110(2);

2)выполнить сложение операндов по правилам двоичной арифметики;

3)к тетрадам суммы, в которых вначале не сформировался

межтетрадный перенос добавить поправку ∆2 = 10(10) = 1010(2) и блокировать передачу возникшей при этом единицы переноса.

Пример 1.6

17

Очевидно, что знак суммы получается автоматически. 3. Выполним вторую коррекцию:

Результаты суммирования в десятичной и двоично-десятич- ной системах счисления совпадают.

Задача 2

1.Разработайте логическую и принципиальную электрическую схему КЦУ, функционирование которого задано таблицей истинности (таблица 2.1).

2.Минимизируйте заданную логическую функцию с помощью карт Карно. Запишите результат минимизации в МДНФ.

3.Постройте логическую схему устройства в базисе И, ИЛИ, НЕ.

4.Запишите результат минимизации через логическую операцию

И-НЕ.

5.Постройте логическую схему устройства в базисе И-НЕ.

6.Постройте принципиальную электрическую схему устройства в базисе И-НЕ на микросхемах схемотехники КМОП, серия которых задана в примечании к таблице 2.1.

7.Проверьте правильность функционирования логических и принципиальной электрической схем КЦУ для пятого набора аргументов и сделайте вывод.

18

8. Определите среднюю задержку распространения сигнала от входов к выходу и среднюю потребляемую мощность в принципиальной электрической схеме КЦУ.

Таблица 2.1 – Исходные данные к задаче 2

Примечание – Для нечетных вариантов принципиальную электрическую схему КЦУ строить на микросхемах серии 1554, для четных – на микросхемах серии 1564.

Методические указания по выполнению задачи 2

Предварительно изучите темы № 1.2 «Логические основы цифровой техники», № 1.3 «Схемотехнические основы цифровой техники» и № 1.4 «Анализ и синтез КЦУ» по [1, с. 31–90].

Рекомендуется следующая методика решения задачи 2.

1. Нанесите значения заданной логической функции на карту Карно и проведите минимизацию. Для построения логической схемы устройства в базисе И-НЕ результат минимизации запишите в минимальной дизъюнктивной нормальной форме (МДНФ). Для записи результата минимизации в МДНФ в замкнутые контуры (области) объединяйте клетки с единичными и неопределенными значениями ЛФ (Ф – неопределенное значение ЛФ). При этом следует помнить, что в

19

замкнутые области можно объединять одну, две, четыре, восемь и т. д.

клеток. В результат минимизации входят только те аргументы,

которые не меняют значение истинности для всех клеток замкнутой области. Если значение аргумента равно 0, то его символ в МДНФ записывается со знаком отрицания. Распределение набо-

ров аргументов по клеткам карты Карно представлено на рисунке 2.1.

Рисунок 2.1 – Распределение наборов аргументов по клеткам карты Карно

2.Для построения логической схемы устройства в базисе И-НЕ результат минимизации необходимо сначала записать в базисе И, ИЛИ, НЕ в МДНФ, а затем полученную ЛФ преобразовать в базис И-НЕ.

3.Рассмотрим пример синтеза КЦУ в базисе И, ИЛИ, НЕ,

функционирование которого задано таблицей истинности (функция

f11(x1, x2, x3) в таблице 2.1).

3.1 Нанесем значения логической функции f11(x1, x2, x3, x4) на карту Карно (рисунок 2.2) и проведем минимизацию, причем результат минимизации запишем в МДНФ.

Рисунок 2.2 – Карта Карно для минимизации логической функции в МДНФ

20