Пример.

Найдем Аккуратно продифференцировав, мы получим, что это выражение равно0, т.е. - гармоническая функция.

Действительно, рассмотрим единичный точечный заряд и функцию. Как известно из физики, эта функция удовлетворяет уравнению Пуассона:

,  = (x), т.к. заряд точечный. И, т.о., и, еслиr 0, то  (x)=0 

§2. Основные определения теории обобщенных функций

Определение 1 (пространство основных функция).

D(R¹) – пространство основных или пробных функций, а именно: пространство бесконечно дифференцируемых функций, имеющих компактный носитель:

Вспомним:

D(R¹) , т.к. ему принадлежит, например, рассматриваемый ранее компакт Шварца.

Определение 2 (сходимость).

Введем в пространстве D(R¹) понятие сходимости.

Пусть {_n} D. Тогда мы скажем, что _nD, если выполняются условия:

1)

2)

Определение 3 (определение обобщенной функции).

Обобщенная функция – это непрерывный линейный функционал на D.

D’={f , f – линейный непрерывный функционал на D} – пространство обобщенных функций.

Замечание (об обычных функциях).

Всякая обычная функция является обобщенной. Под обычной функцией мы будем понимать функцию f (x), которая локально и абсолютно интегрируема по времени.

Если f – обычная, тогда соответствующая обобщенная функция определяется так:

Обычные функции называются обобщенно регулярными.

Обобщенные функции, не являющиеся обычными, называются сингулярно обобщенными. Примером может служить  -функция Дирака.

§3. Свойства обобщенной - функции Дирака

Предварительное уведомление.

Большинство описанных здесь свойств будет объяснено и обобщено в последующих параграфах.

Вариант определения - функции.

Вариант записи:

Производная- функции.

Первообразная от- функции.

- «тета»-функция.

Умножение на гладкую (бесконечно дифференцируемую) функцию.

Серьезной проблемой является нахождение Классическая математика не в состоянии этого сделать.

Носитель - функции.

Для всех других

Замена переменных.

Рассмотрим  (g(x)).

Тогда полагаем:

Пример 1.

g(x)=ax. Покажем это.

Пример 2.

Пример 3.

Покажем, что  (x₂+1) 0.

Пусть Тогда:

. Обоснуем исходя из свойства носителя  - функции:

Преобразование Фурье - функции.

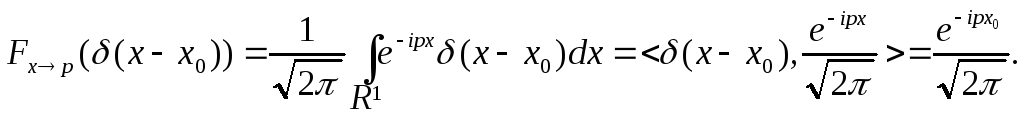
Положим x₀=0 

Формулы Сохоцкого.

, где вD’.

, где

- интеграл в смысле главного значения. Он не совпадает с несобственным интегралом. Так, хотя - не суммируемая в нуле и на бесконечности функция в смысле несобственного интеграла, но:

, т.к.

 -функция, как слабый предел -образной последовательности.

Пусть Последовательностьназывается - образной, если выполняются условия:

1)

2)

Примеры.

1) Используется в процессах тепломассопереноса.

2) . Используется в радиотехнике, теории связи.

3) . Используется в оптике, распространении электромагнитных волн.

Задача.

Доказать, что 2), 3) -  -образные последовательности.

§4. Дифференцируемость вD’

Предварительное замечание.

Пусть f D’. Чему равна производная этой обобщенной функции?

Пусть этой обобщенной функции соответствует обычная функция f (x)(C¹(R¹)):

.

Тогда определена ее производная . Естественным путем поставим этой производной функционал и найдем его:

Определение 1 (производная обобщенной функции).

Пусть f D’. Тогда определена ее производная:

Данное определение корректно, т.е. правая часть – линейный непрерывный функционал на D.

Следствие (о бесконечной дифференцируемости обобщенной функции).

Пусть f D’.

Тогда , т.е. любая обобщенная функция бесконечное число раз дифференцируема вD’, и ее k-ая производная определяется так:

Пример (тета-функция).

Как обычная функция, тета-функция не дифференцируема в нуле. Найдем ее производную, как производную обобщенной функции.

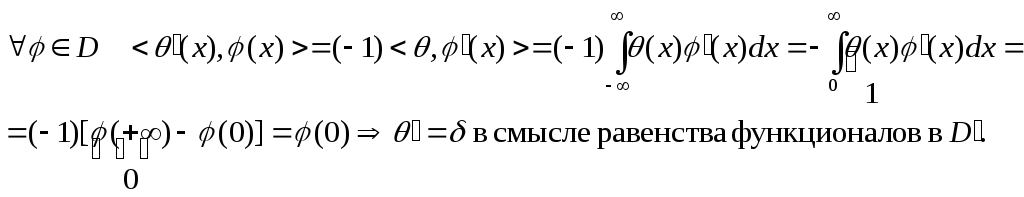
Теорема (о дифференцировании кусочно-гладкой обобщенной функции).

Пусть f (x) – кусочно-гладкая (кусочно-дифференцируемая с разрывами 1-го рода). Будем считать без нарушения общности, что разрыв только в точке x₀. Т.о.

Обозначим .

Тогда в пространстве D’

Доказательство.

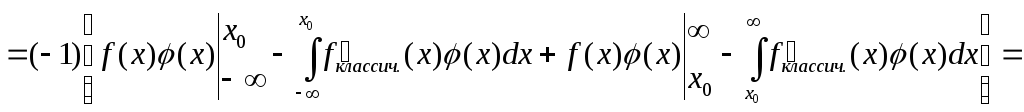
§5. Умножение вD’

Пусть f D’. Дана функция Требуется определить

Определение 1 (умножение на функцию).

Определение корректно, т.к. D  g(x)D.

Пример 1.

Рассмотрим

Пример 2.

g(x) (x)=g(0) (x).

Теорема 1 (правило Лейбница).

Имеет место равенство:

Доказательство.

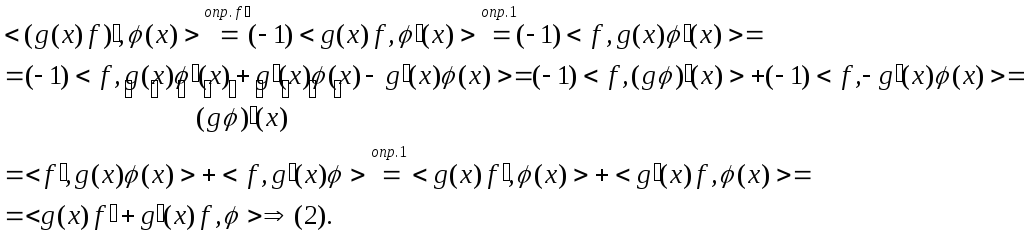
Пример 3.

Это также можно доказать из уже доказанного факта о том, что x(x)=0. Действительно, тогда

Пример 4.

Рассмотрим функциональное уравнение xy(x)=0

Как видно, с классической точки зрения решение этого уравнения не определено в нуле.

Рассмотрим это уравнение с точки зрения обобщенных функций.

xy(x)=0, y(x)D’. Из примера 1 следует, что y(x)=(x) удовлетворяет этому уравнению, и y(x)=C(x) также решение этого уравнения.

Замечание.

Других решений у этого уравнения нет (без доказательства).

Пример 5.

Почему g(x)f определено лишь для g(x)C^(R¹)?

Пусть g C^(R¹). Если аналогичным образом определить операцию умножения на эту функцию, то, оказывается, можно доказать, что 0=1 (!).

Действительно, возьмем(x) такую, чтобы:

Вспомним о обобщенной функции .

Очевидно, что Рассмотрим:

Тогда:

, но согласно полученному:

Возникшее противоречие связано с тем, что равенство помеченное, как «?!», неверное в связи с тем, что

§6. Замена переменных вD’

Определение (линейная замена переменных).

Пусть Тогда положим по определению:

Если f – обычная функция, то (1) превращается в равенство, если обобщенная, то это определение.

Замечание 1 (о корректности определения).

Определение корректно. Действительно,, т.к. это та же самая функция , но смещенная вправо на b и сжатая в a раз.

-

Замечание 2.

.

Если b=0, то

Если a= -1, то (-x)=(x), т.е. (x) – четная функция.

Теорема (замена переменных в функции Дирака).

Если g(x) – не линейная функция, но гладкая (бесконечно дифференцируема), то для (x) можно определить (g(x)) в случае, когда выполняется следующее условие:

В этом случае имеет место формула:

.

Доказательство

I. Пусть g(x)0 x. Тогда очевидно, что (g(x))=0 (доказывается аналогично примеру 3 из §3).

II.Пусть J={x₀} т.е. состоит из одной точки. g(x₀)=0, g’(x₀)0. Пусть g’(x)>0.

.

Т.к. g’(x)>0, то (Im – обозначение образа).

1)x₀[a,b]

Т.о. g ^-1(t)0, t[g(a), g(b] 

2) x₀[a,b].

III. Пусть теперь

{x_j} – нули первого порядка.

Эту часть мы докажем исходя из следующей леммы.

Лемма (о разбиении единицы).

Существует разбиение единицы, т.е.

Пусть -интервалы, покрывающие все R¹, такие, что для j’=j=1,2,…,M x_jV_j, т.е. V_j содержит ровно один корень g(x), а не содержит ни одного корня.

Причем j’ J – счетное множество и попарно пересекаются.

Тогда существует набор функций , подчиненный разбиению, т.е.:Причем

Разобьем R¹на интервалы, указанные в лемме, причем так, чтобы нафункцияg(x)была бы монотонной.

Объяснение последнего равенства:

, т.к.

Т.о. теорема доказана.