94

Лекция № 1. ПОНЯТИЕ СЛУЧАЙНОГО ПРОЦЕССА

Пусть задано ( Ω, А, Р ) – вероятностное пространство.

Случайная величина ξ = ξ (ω) : Ω → R, для которой выполнено : для  борелевского множества В  В,

В – борелевская  - алгебра (сигма-алгебра с интервалами) в R , выполнено ξ^{– 1}(В) = {ω   :  ()  В  А.

Таким образом,  () - измеримая или (А, В) измеримая функция.

Измеримость заключается в том, что множество ξ^{– 1}(В) имеет меру.

Определение1. Случайным процессом называется семейство случайных величин

ξ ( t ) = ξ (ω, t), t  ,   Ω ( Т – время), заданных на одном и том же вероятностном пространстве (Ω, А, Р).

Конструкции:

1. Т может быть конечно. Т = {0, 1, 2 …, n, тогда случайные процессы {ξ _0, ξ _{1 …,} ξ _n - система случайных величин.

2. Т = {0, 1, 2 … - счетное; случайный процесс {ξ _n , n ≥ 0 - последовательность случайных величин (дискретная случайная величина).

3. Т = 0, ) – непрерывный случайный процесс с непрерывным временем.

Лекция № 2.

х

t (диск.)

Рис. 1. Траектория процесса выпуска автомобилей

х

t (диск.)

Рис. 2. Траектория курса акций на фондовой бирже

Случайный процесс представляет собой семейство случайных величин ξ ( t )= ξ(ω, t ),

t   (время),    (элементарный исход). Для  фиксированного t   ξ(ω, t ) – случайная величина.

Для  фиксированного    структура ξ(ω, t), t   является функцией, которая называется траекторией (реализацией) случайного процесса.

Рассмотрим второй подход к определению случайного процесса, который состоит в построении измеримого отображения ξ : Ω → Х (множество возможных траекторий процесса).

Это аналогия с понятием случайной величины.

Этот процесс называется непосредственно заданным случайным процессом.

Пусть ( , А, Р ) – вероятностное пространство.

Построим выборочное вероятностное пространство или пространство траекторий процесса.

1. Пусть Х = { х ( t ), t    - множество всех возможных функций заданных на Т со значением в Х. В роли Х может выступать конечное множество, счетное или нечто более сложное, непрерывное.

2. Построим  - алгебру подмножеств множества Х, при этом подразумеваем, что в Х  - алгебра уже есть.

Пусть С = С_t1, …, _tn (В_{1 …,} В_n) = { х ( )  Х : х ( t₁ )  В_1, …, х ( t n), t  В_n 

функция целиком

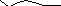
Х	B1		B2	Bn	.
	t1 t2 tn T

Множество функций, проходящих через эти ворота, называются цилиндрическим.

Цилиндрическое множество в Х.

В₁, _…, В_n  В –  - алгебра подмножеств в Х.

(если Х = R, то В – борелевская)

Заметим, что конечное пересечение и объединение множеств цилиндрического характера образуют сигма – алгебру ( - алгебру). Алгебра цилиндрических множеств .

Нужно построить эту -алгебру . Рассмотрим все  - алгебры, содержащие . Рассмотрим пересечение всех  - алгебр. Это пересечение является  - алгеброй, оно является наименьшей  - алгеброй, содержащей . И называется  - алгеброй, порожденной цилиндрическими множествами.

 ( ) = F

Итак, имеем пару ( Х, F), которая образует измеримое пространство.

Можно строго определить измеримое отображение.

Определение 2. (фундаментальное) Случайным процессом называется измеримое отображение ξ : Ω → Х, т.е. для  В  F : ξ^{– 1}(В)  А, ξ^{– 1}(В) – прообраз

3. к определению выборочного вероятностного пространства.

Т.к. мера задана по А, то зададим вероятностную меру на F :

Р_ξ (В) = Р ( ξ^{– 1}(В) )

Эта мера называется индуцируемой ( мера Р индуцирует (порождает) меру Р_ξ ).

Итак, построено три объекта ( Х, F, Р_ξ ), которые составляют вероятностное пространство, его называют выборочное пространство или пространство траекторий. Можно также себе представить, что реализация случайных процессов – это реализация случайного эсперимента на ( Х, F, Р_ξ ).

Пусть В = С = С_t1, …, _tn (В_{1 …,} В_n) (цилиндрическое). Тогда из определения следует

Р_ξ (В) = Р_ξ (С_t1, …, _tn (В_{1 …,} В_n) ) = Р ( ξ^{– 1} (С_t1, …, _tn (В_{1 …,} В_n) ) ) = Р (ω   :  ()  С_t1, …, _tn (В_{1 …,} В_n) ) = Р (ω   :  (, t₁)  В_{1 …,}  (, tn)  В_n) – определена.

Замечание

 () ( t ) =  (, t ) – значение функции в точке t.

Эта вероятность Р_ξ (В) называется конечномерным распределением случайного процесса. Если этот процесс рассматривать при всех t₁, …, tn  Т, В_{1 …,} В_n  В, то это будет семейство конечномерных распределений данного случайного процесса.

Введем еще одно дополнительное понятие.

Будем обозначать через { F_t1, …, _tn (В_{1 …,}В_n )_, t₁, …, t_n  Т; В_{1 …,} В_n  В , n ≥ 1  = Fт (В) семейство вещественных функций, заданных на В_{1 …,} В_n и зависящих от параметров t₁, …, tn.

Лекция № 3

Зададим семейство функций:

F_т (В) = { F_t1, …, _tn (В_{1 …,}В_n )_, t₁, …, t_n  Т; В_{1 …,} В_n  В , n ≥ 1 , зависящих от параметра t и переводящих борелевские множества в R^-1.

В –  - алгебра (борелевская) в Х.

Определение. Семейство функций F_т (В) называется семейством согласованных вероятностных мер, если оно обладает следующими свойствами:

1. для  набора параметров ( t₁, …, t_n ) наша функция F_t1, …, _tn (В_{1 …,} В_n) представляет собой вероятностную меру (совместное распределение).

2. для  перестановки ( i₁ , i₂, …, i_n ) чисел (1, 2, …n) имеет место следующее равенство:

F _i1, t i ₂…, t _{i n} (В _{i 1} , В _{i 2 …,}В _{i n} ) = F _{t 1}, t₂…, t n (В₁ , В_{2 …,}В_n ).

3. F_t1, t _n-1…, t _n (В₁ , _…,В _n-1, Х ) = F_t , …, t _{n -1} (В₁ ,_…,В_n-1 )

(понижение размерности функций).

Все эти свойства характерны для совместного распределения (конечномерного).

Теорема (Колмогорова)

Для того, чтобы существовал случайный процесс, у которого заданное семейство функций F_т (В) было бы семейством конечномерных распределений необходимо и достаточно, чтобы это семейство являлось бы семейством согласованных вероятностных мер.

Иначе. Если F_т (В) – семейство согласованных вероятностных мер, то найдется такой случайный процесс для которого эти функции являются семейством конечномерных распределений.

В качестве выборочного вероятностного пространства (пространство траекторий) выбирается:

Х = {х ( t ), t  Т со значением в Х}–

множество всех функций на Т со значением в Х;

F –  - алгебра, порождаемая цилиндрическими множествами;

мера на F: Р (С) = Р (х ( · )  Х : х ( t₁ )  В₁, …, х ( t _n)  B_n ) = F_t1, …, _tn (В_{1 …,} В_n).

Тогда каждая траектория случайного процесса совпадает с реализацией случайного эксперимента на вероятностном пространстве ( Х, F, Р ), т.е. формально можно записать так:  (, t ) = х ( t ).

Замечание к теореме.

1. Теорема Колмогорова представляет собой теорему существования, при этом теорема не утверждает единственность такого процесса. Объективно может существовать несколько случайных процессов, имеющих одно и тоже семейство конечномерных распределений.

Определение. Случайные процессы ₁, ₂ , имеющие одно и тоже семейство конечномерных распределений называются стахостически эквивалентными.

Иногда также говорят, что эти процессы являются модификациями некоторого одного случайного процесса.

Иначе говоря, для стохастических эквивалентных процессов ₁ ( t ), ₂ ( t ) справедливо следующее соотношение Р ( ₁ ( t ) = ₂ ( t ) ) = 1, t  Т ( с вероятностью 1, их значения совпадают).

2. Множество функций Х (т.е. множество возможных траекторий) слишком широко для описания процесса. Для более детального анализа процесса, желательно знать более определенные свойства траекторий. Поэтому в теории случайных процессов доказывают результаты о характере траекторий тех или иных классов случайных процессов.

Теорема (А.Н. Колмогорова) о существовании непрерывной модификации случайного процесса.

Предположим, что для всех случайных процессов  ( t ) при всех значениях t , t + h  Т справедлива следующая оценка:

М |  ( t + h) -  ( t ) | ^а ≤ с | h | ^{1 + b}

для некоторых а > 0, b > 0, с < ∞, М – мат. ожидание. Тогда случайный процесс  ( t ) имеет непрерывную модификацию, т.е. почти все траектории этого процесса представляют собой непрерывные функции.

Определение. Случайный процесс  ( t ) называется стахостически непрерывным, если  t  Т и h → 0 и для произвольного малого Ε > 0, вероятность

Р = ( |  ( t + h ) -  ( t ) | > E ) → 0, h → 0.

Иначе говоря :  ( t + h ) ^р  ( t ),

т.е.  ( t + h ) и  ( t ) сходятся по вероятности.

Если  ( t + h ) сходятся к  ( t ) в среднеквадратичном, то процесс называется стахостически непрерывным в среднеквадратичном.