3.3.3. Доверительный интервал для дисперсии нормальной св

Пусть X~N(m, ), причем m и – неизвестны. Пусть для оценки извлечена выборка объема n:

1.В качестве точечной оценки дисперсии D(X) используется исправленная выборочная дисперсия которой соответствует стандартное отклонение .

2.При нахождении доверительного интервала для дисперсии в этом случае вводится статистика , имеющая - распределение с числом степеней свободы 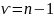независимо от значения параметра

3.Задается требуемый уровень значимости α.

4.Тогда, используя таблицу критических точек - распределения, нетрудно указать критические точки . (3.8)

Подставив вместо соответствующее значение, получим

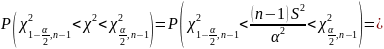
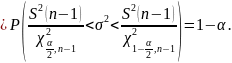(3.9)

Неравенство может быть преобразовано в следующее:

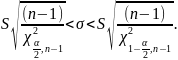(3.10)

Таким образом, доверительный интервал

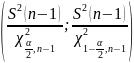
Накрывает неизвестный параметр с надежностью .

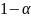А доверительный интервал 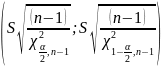c надежностью накрывает неизвестный параметр σ.

3.4. Статистическая проверка гипотез

3.4.1. Основные понятия

Большинство эконометрических моделей требуют много­кратного улучшения и уточнения. Для этого необходимо прове­дение соответствующих расчетов, связанных с установлением выполнимости или невыполнимости тех или иных предпосы­лок, анализом качества найденных оценок, достоверностью по­лученных выводов. Обычно эти расчеты проводятся по схеме статистической проверки гипотез. Поэтому знание основных принципов проверки гипотез является обязательным для эко-нометриста.

Во многих случаях необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвес­тен, но есть основания предположить, что он имеет определен­ный вид (назовем его А), выдвигают гипотезу: генеральная со­вокупность (СВ X) распределена по закону А. Например, можно выдвинуть предположение, что доход населения, ежедневное количество покупателей в магазине, размер выпускаемых дета­лей имеют нормальный закон распределения.

Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предполо­жить, что неизвестный параметр θ равен ожидаемому числу , выдвигают гипотезу: 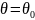- Например, можно выдвинуть предположение о величине среднего дохода населения, средне­го ожидаемого дохода по акциям, о разбросе в доходах и т.д.

Статистической называют гипотезу о виде закона распре­деления или о параметрах известного распределения. В первом случае гипотеза называется непараметрической, а во втором — параметрической.

Гипотеза 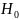, подлежащая проверке, называется нулевой (основной). Наряду с нулевой рассматривают гипотезу Н\, кото­рая будет приниматься, если отклоняется . Такая гипотеза называется альтернативной (конкурирующей). Например, если проверяется гипотеза о равенстве параметра θ некоторому зна­чению , т.е. , то в качестве альтернативной могут рассматриваться следующие гипотезы:

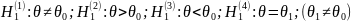
Выбор альтернативной гипотезы определяется конкретной формулировкой задачи, а нулевая гипотеза часто специально подбирается так, чтобы отвергнуть ее и принять тем самым аль­тернативную гипотезу. Для того чтобы принять гипотезу о на­личии корреляции между двумя экономическими показателя­ми (например, между инфляцией и безработицей), можно опровергнуть гипотезу об отсутствии такой корреляции, взяв ее в качестве нулевой гипотезы.

Гипотезу называют простой, если она содержит одно кон- кретное предположение (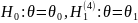 ). Гипотезу на- зывают сложной, если она состоит из конечного или беско- нечного числа простых гипотез :

Сущность проверки статистической гипотезы заключается в том, чтобы установить, согласуются или нет данные наблюдений и выдвинутая гипотеза. Можно ли расхождение между гипоте­зой и результатом выборочных наблюдений отнести за счет слу­чайной погрешности, обусловленной механизмом случайного от­бора? Эта задача решается с помощью специальных методов математической статистики — методов статистической провер­ки гипотез.

При проверке гипотезы выборочные данные могут противо­речить гипотезе . Тогда она отклоняется. Если же статисти­ческие данные согласуются с выдвинутой гипотезой, то она не отклоняется. В последнем случае часто говорят, что нулевая гипотеза принимается (такая формулировка не совсем точна, однако она широко распространена). Статистическая проверка гипотез на основании выборочных данных неизбежно связана с риском принятия ложного решения. При этом возможны ошиб­ки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза.

Ошибка второго рода состоит в том, что будет принята ну­левая гипотеза, в то время как в действительности верна аль­тернативная гипотеза.

Возможные результаты статистических выводов представ­лены следующей таблицей:

Результаты проверки гипотезы	Возможные состояния гипотезы
	верна	верна
Гипотеза отклоняется Гипотеза не отклоняется	Ошибка первого рода Правильный вывод	Правильный вывод Ошибка второго рода

Последствия указанных ошибок неравнозначны. Первая приводит к более осторожному, консервативному решению, вторая — к неоправданному риску. Что лучше или хуже — за­висит от конкретной постановки задачи и содержания нулевой гипотезы. Например, если Но состоит в признании продукции предприятия качественной и допущена ошибка первого рода, то будет забракована годная продукция. Допустив ошибку вто­рого рода, мы отправим потребителю брак. Очевидно, последст­вия второй ошибки более серьезны с точки зрения имиджа фир­мы и ее долгосрочных перспектив.

Исключить ошибки первого и второго рода невозможно в силу ограниченности выборки. Поэтому стремятся минимизи­ровать потери от этих ошибок. Отметим, что одновременное уменьшение вероятностей данных ошибок невозможно, так как задачи их уменьшения являются конкурирующими, и сниже­ние вероятности допустить одну из них влечет за собой увеличе­ние вероятности допустить другую, В большинстве случаев единственный способ уменьшения вероятности ошибок состоит в увеличении объема выборки.

Вероятность совершить ошибку первого рода принято обо­значать буквой а, и ее называют уровнем значимости. Вероят­ность совершить ошибку второго рода обозначают р. Тогда веро­ятность не совершить ошибку второго рода (1 — β) называется мощностью критерия.

Обычно значения а задают заранее, «круглыми» числами (например, 0,1; 0,05; 0,01 и т.п.), а затем стремятся построить критерий наибольшей мощности. Таким образом, если α = 0,05, то это означает, что исследователь не хочет совершить ошибку первого рода более чем в 5 случаях из 100.