6. Обратная матрица и её вычисление.

Определение. Матрица В называется обратной по отношению к матрице А, если

.

Из определения следует, что если матрица А имеет обратную, то обе они должны быть квадратными матрицами одного порядка.

Из определения следует, что если матрица В является обратной по отношению к матрице А, то и матрица А является обратной по отношению к матрице А.

Определение. Матрица имеющая обратную матрицу называется обратимой.

Теорема. Если квадратная матрица А имеет обратную, то она единственная.

Доказательство. Пусть В и С - две матрицы обратные к матрице А. Тогда и . Имеем,

, ч.т.д.

7. Матричный метод, решение системы линейных ур-ний

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с   неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:

, где   — основная матрица системы,   и   — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на   — матрицу, обратную к матрице  : 

Так как  , получаем  . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

Для однородной системы линейных уравнений, то есть когда вектор  , действительно обратное правило: система   имеет нетривиальное (то есть ненулевое) решение только если  . Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Введем матрицу системы

и матрицы   и  . Пусть  .

Представим систему (1.10) в виде матричного уравнения АХ=В. Это легко проверить, перемножив матрицы А и Х.

Действительно,

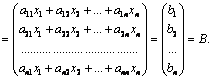
Решим теперь матричное уравнение А·Х=В. Умножим обе части уравнения на матрицу А-1 слева. Тогда А-1·А·Х = А-1·В, а так как

А-1·А=Е, то имеем Е·Х=А-1·В и, наконец,

Х = А-1·В                                           

8. Определение функций. Способы задания функции.

Функция (отображение, оператор, преобразование) - математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция - это "закон", по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной однозначно определяет значение выражения , а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека - его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином "функция" понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

Функция может быть определена разными формулами на разных участках области своего задания.

Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа - основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Пример 1: функция E(x) - целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, гдеr - целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [x] = r. Функция E(x) = [x] постоянна на промежутке [r; r+1) и на нем [x] = r.

Пример 2: функция y = {x} - дробная часть числа. Точнее y ={x} = x - [x], где [x] - целая часть числа x. Эта функция определена для всех x. Если x - произвольное число, то представив его в виде x = r + q ( r = [x]), где r - целое число и q лежит в интервале [0; 1), получим {x} = r + q - r=q

Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.

9. Основные элементарные функции, их св-ва и графики, обратная функция.

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:

алгебраические:,степенная;рациональная.,трансцендентные: показательная и логарифмическая;

тригонометрические и обратные тригонометрические.

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

Мы будем акцентировать внимание на следующем:

- область определения и значения функции;

- четность, нечетность функции;

- периодичность;

- монотонность;

- ограниченность;

- точки пересечения с осями координат;

- график функции.

Линейная функция y = kx + b.

la. Рассмотрим вначале частный случай функций y = kx + b при b = 0.

Функция определена при всех

Областью значения является множество R (так как уравнение kx = c имеет решение при всех с).

Функция является нечетной, f(—x) = - kx = - f(x).

Функция не является периодической, так как k(x+T) = kx => kx + kT = kx => кТ = 0 => Т = 0.

Функция не ограничена.

Функция монотонная (при к > 0 возрастающая, k < 0 убывающая).

Е сли у = 0, то х = 0.

1 б. Рассмотрим частный случай функции y = kx + b при k = 0.

у = b.

Эта функция определена при всех

Областью значения является одна точка b.

Функция четная.

Функция периодическая (периодом является любое число, основного периода нет).

Функция ограничена.

Функция постоянная.

1 в. Функция y = kx + b.

Ф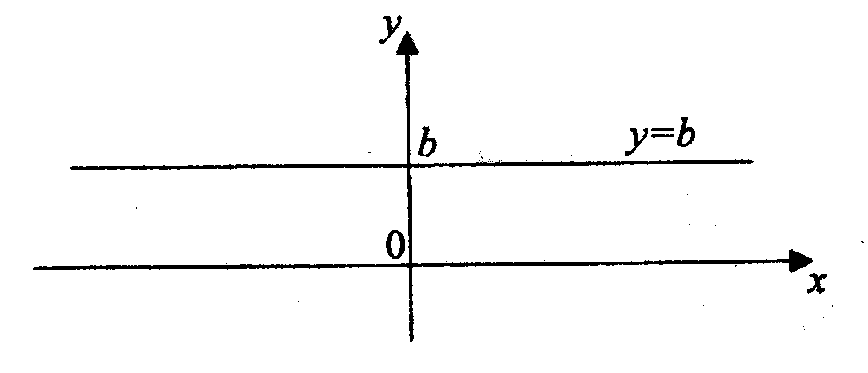 ункция y = kx + b является суммой двух функций y = kx и у = b. Следовательно область определения R (множество действительных чисел).

Область значения R.

Функция общего вида при

Функция не является периодической.

Функция не ограничена.

Функция монотонна (k > 0 возрастающая, k < 0 убывающая).

Г рафик функции получается из графика функции y = kx сдвигом по оси ординат на величину b.

Дробно - линейная функция

а, b, с, d - постоянные, причем (иначе мы имели бы линейную функцию) и (иначе произошло бы сокращение и мы получили бы постоянную функцию).

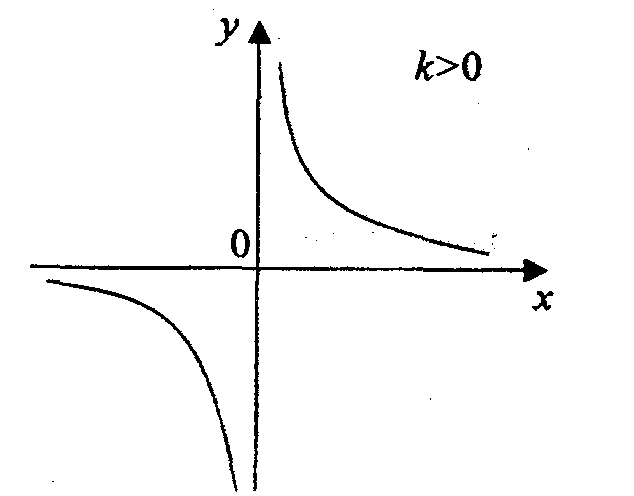
l a. В начале рассмотрим функцию

Функция определена всюду, кроме х = 0, то есть область определения интервалы .

Область значения также интервалы .

Функция нечетная, так как

Функция убывающая (при к > 0) и возрастающая (при k < 0) на интервалах .

Функция неограниченная.

Полученная кривая называется гиперболой.

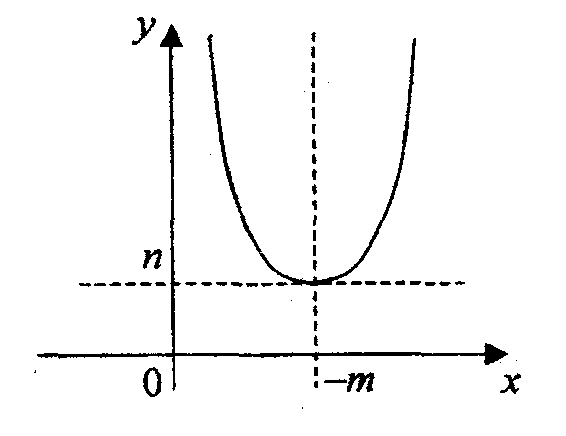
1б. Общий случай

Полагая получаем

Следовательно график функции легко получить из графика функции с помощью сдвига на - т вдоль оси Ох и на n единиц вдоль оси Оу.

Свойства функции получаем из свойств функции

Квадратный трехчлен

( , иначе функция линейная).

1а. Квадратная функция у=ах2.

Функция определена при всех х.

О бласть значения неотрицательные числа (при a > 0) неположительные числа при а < 0.

- функция четная

- функция не является периодической

- функция ограничена снизу при а > 0, ограничена сверху при а < 0

- функция убывает на интервале ( ; 0) при a > 0

возрастает при a < 0

возрастает на интервале (0; ) при а > 0

убывает при а < 0.

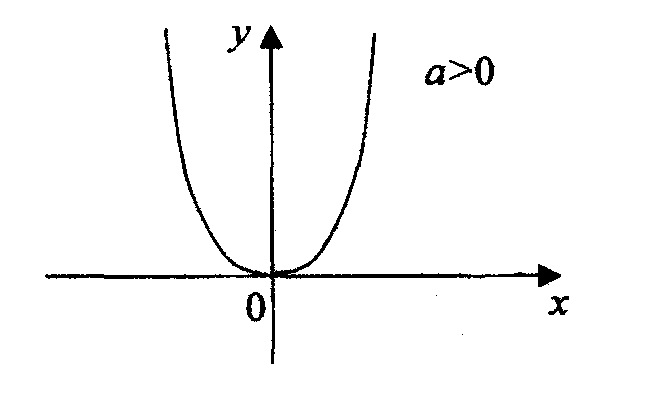
1б. Общий случай .

Получим : Полагая получим

График данной функции получается из графика функции у = ах2

сдвигом на - т по оси Ох и сдвигом на п по оси Оу.

Степенная функция у = хn.

1а. Рассмотрим случай n = 2k.

Функция определена на всей числовой оси.

Функция четная, так как

Функция не является периодической.

На интервале (- ; 0) функция убывает, на интервале (0; + ) функция возрастает.

Функция ограничена снизу.

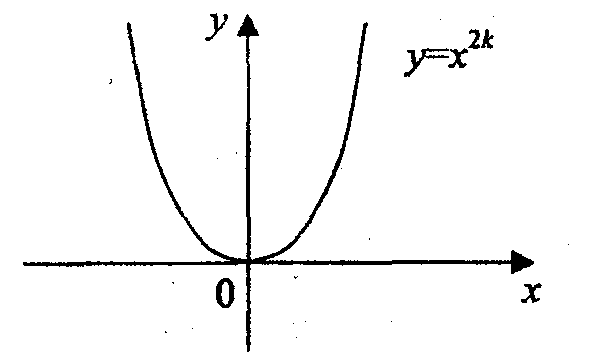
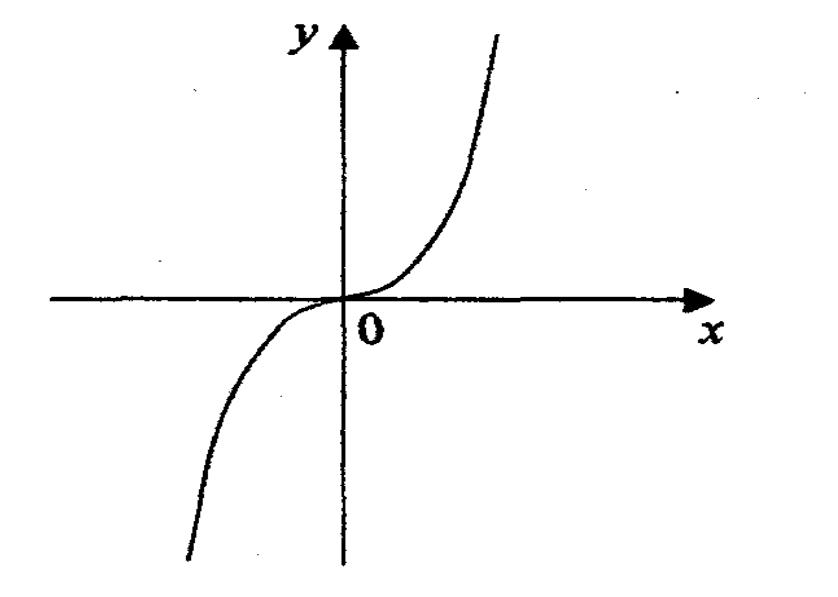
1б. Случай n = 2k + 1, y = x2к+1 .

Функция определена всюду.

Функция нечетная.

Функция не является периодической. Возрастает на всей числовой оси.

Функция не ограничена.

Обратная функция

Пусть на некотором множестве Х задана функция у = f(x) и Y - область значения данной функции.

Возьмем некоторое число . Тогда найдется такое число (возможно не единственное), что Таким образом, каждому значению поставлено в соответствие число (возможно не единственное). Если такое число - единственное, то говорят, что задана функция х = g(y).

/Для существования обратной функции необходимо и достаточно, чтобы функция у = f(x) осуществляла взаимно-однозначное соответствие между множествами Х и Y./

Графики функции у = f(х) и обратной для нее функции х = g(y) совпадают, только аргумент обратной функции рассматривается на оси Оу.

Но если, следуя нашим привычкам, аргумент обозначить буквой х и откладывать его на оси Ох, то есть вместо х = g(y) писать у = g(x), то график функции у = g(x) отличается от графика функции у = f(х).

Легко показать, что графики функции у = f(x) и обратной к ней функции

у = g(x) симметричны относительно биссектрисы I и III координатных углов.

Заметим, что и свойства прямой, и обратной функций связаны между собой.

1. Область определения функции у = f(х) Х является областью значений функции .

Область значения функции у = f(x) Y является областью определения функции .

3. Если функция у =f(х) возрастает (убывает), то функция y = g(x) возрастает (убывает).

4. Если функция у = f(х) дифференцируема в точке , то функция у = g(x) дифференцируема в точке

10. Элементарная функция, сложная функция.

Сложная функция - функция от функции. Если z - функция от у, т.е. z(y), а у, в свою очередь, - функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

В такой функции х - независимая, а у - промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).

Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:

.

Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов ("цепное правило"): если z = f1(y1),y1 = f2(y2), …, yn-1 = fn(x), то

11. Определение числовой последовательности. Способы задания, арифметич.

прогрессиия и геометрич. прогрессия.

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ - функция вида y = f(x), x ? N,где N - множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,…называют соответственно первым, вторым, третьим, … членами последовательности.

Функцию y=f(x), x ? N ( Напомню, что N это натуральные числа, то есть числа от 1 до 9) называютфункцией натурального аргумента или же числовой последовательностью. Её обозначают следующим образом: y=f(n) или y1, y2, y3...,yn или (yn).

Ну а теперь давайте перейдём непосредственно к тем способам, которыми можно задать числовую последовательность.

Первый способ самый простой - словесный. Он используется, когда правило задания последовательности описано словами, не указывая формулы. Таким способом можно к примеру задать следующую последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,...

Второй способ - аналитический. Когда числовая последовательность задана формулой n-ного члена. Для наглядности я приведу три примера:

yn=n2 Это аналитическое задание последовательности чисел: 1, 4, 9, 16, 25...,n2,... Указав конкретное значение n, нетрудно найти член последовательности с соответствующим номером. К примеру нам нужно найти 10 член последовательности, значит n=10. Отсюда y10=102, а значит 10 член последовательности равен 100.

yn=C такая формула говорит нам о последовательности, которая имеет следующий вид: C, C, C, C,... такую последовательность называют постоянной или стационарной.

yn=2n это аналитическое задание последовательности 2, 22, 23, 24,...

3. Третий способ на мой взгляд самый интересный - это рекуррентный способ. Не пугайтесь этого слова, оно означает что нам даётся правило по которому можно вычислить следующие члены последовательности зная предыдущие. Заметьте, что именно правило а не формула, это очень важно! Далее я приведу три примера рекуррентного способа задания числовой последовательности.

Арифметическая прогрессия. Я уверен. что она знакома вам ещё с восьмого класса, она задана рекуррентно соотношениями: а1=а, аn+1=an+d (Где d - разность арифметической прогрессии, a и d - заданные числа)

Геометрическая прогрессия. Она вам тоже несомненно знакома, она рекуррентно задана соотношениями: b1=b, bn+1=bn*q (Где a и q - заданные числа, причём b?0 и q?0; q - знаменатель геометрической прогрессии).

Последовательность Фибоначи. Это возможно новое для вас понятие, но эта последовательность очень проста, каждый последующий её член равен сумме двух предыдущих. Она задана рекуррентно следующими соотношениями: b1=1, b2=1 bn=bn-2+bn-1Приведу начало этой последовательности для наглядности 1, 1, 2, 3, 5, 8, 13, 21...

Если каждому натуральному числу n (n = 1, 2,...) поставлено в соответствие число xn, то говорят, что задана числовая последовательность x1, x2,..., xn..., обозначаемая {xn}. Числаx1, x2,..., xn... называются членами последовательности, а член с номером n - ее n-м членом.

Арифметическая прогрессия

Числовую последовательность {an}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называют арифметической прогрессией. Число d называется разностью арифметической прогрессии: an+1 = an + d. Число Sn называется суммой n первых членов арифметической прогрессии.

Свойства арифметической прогрессии:

Геометрическая прогрессия

Числовую последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ? 0, называют геометрической прогрессией.

Число q называется называется знаменателем прогрессии: bn+1 = bnq.

Число Sn называется суммой n первых членов геометрической прогрессии, Pn - произведением n первых членов геометрической прогрессии.

Свойства геометрической прогрессии:

12. Определение предела ЧП.

Предел числовой последовательности - предел последовательности элементов числового пространства. Числовое пространство - это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому,

предел числовой последовательности - это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.

Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.

Предел (числовой последовательности) - одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений.[1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.

Определение. Число А называется пределом последовательности , если для любого положительного числа существует такой номер N, зависящий от , что для всех номеров выполняется условие .

Обозначение: или при .

Определение. Последовательность, имеющая предел (из определения ясно, что A - конечно), называется сходящейся.

Определение. Если , то называется бесконечно малой последовательностью.

Определение. Последовательность называется бесконечно большой, если для любого положительного числа M существует такой номер N, зависящий от M, что для всех номеров выполняется условие .

В этом случае говорят, что предел равен бесконечности и обозначают .

Определение. Последовательность, не являющаяся сходящейся, называется расходящейся.

Очевидно, что бесконечно большая последовательность является расходящейся.

13. Признак Бирштрасса, существование конечного предела ЧП.

Теорема Больцано - Вейерштрасса, или лемма Больцано - Вейерштрасса о предельной точке - предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства можно выделить сходящуюся подпоследовательность. Теорема Больцано - Вейерштрасса, в особенности случай числовой последовательности ( ), входит в каждый курс анализа. Она используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема носит имена чешского математика Больцано и немецкого математика Вейерштрасса, которые независимо друг от друга её сформулировали и доказали. В зависимости от признака, по к-рому производится выбор отрезковпри применении Б.-В. п. в., получается либо эффективный процесс, либо неэффективный. Примером первого случая является применение Б.-В. <п. в. к доказательству существования у непрерывной действительной функции, принимающей на концах нек-рого отрезка значения разного знака, точки на этом отрезке, в к-рой она обращается в нуль (см. Ноши теорема о промежуточных значениях непрерывной функции). В этом случае признаком, по к-рому производится последовательный выбор отрезков, является наличие у функции значений разных знаков на концах выбираемых отрезков. Если имеется способ вычисления функции в каждой точке, то в результате достаточно большого числа шагов можно получить координату точки, в к-рой функция на рассматриваемом отрезке обращается в нуль, с любой наперед заданной точностью. Таким образом, в этом случае одновременно с доказательством существования корня уравнения на отрезке, на концах к-рого функция принимает значения разных знаков, дается и метод приближенного решения этого уравнения. Примером второго случая является доказательство с помощью Б.-В. п. в. теоремы о достижимости действительной непрерывной на отрезке функцией ее верхней грани. Здесь при последовательном делении : отрезков пополам выбирается тот отрезок, на к-ром верхняя грань значений функции не меньше, чем на втором. Если, как и в первом случае, известен способ вычисления функции в каждой точке, то этого недостаточно для эффективного выбора нужного отрезка. .Поэтому в этом случае с помощью В.- В. п. в. можно лишь доказать теорему существования, утверждающую, что рассматриваемая функция принимает в нек-рой точке свое наибольшее значение, а не получить метод для приближенного отыскания с наперед заданной точностью этой точки.

Имеются различные обобщения Б.-В. <п. <в., напр, на случай re-мерного евклидова пространства применительно к n-мерным кубам при последовательном их делении на конгруэнтные кубы с ребрами, вдвое меньшими ребер исходного куба. Л. Д. Кудрявцев.

14. Определение предела функции на бесконечности.

Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) - b| < ?. Запись этого факта:

Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа ? < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < -M, выполняется неравенство |f(x) - b| < ?. Записывается это так:

15. Определение предела функции в точке.

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, - такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки - частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе "стремление аргумента к бесконечности".

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказываетсянепрерывной (в данной точке).

Определения

Рассмотрим функцию  , определённую на некотором множестве  , которое имеет предельную точку   (которая, в свою очередь, не обязана ему принадлежать).

[править]Предел функции по Гейне

Значение   называется пределом (предельным значением) функции   в точке  , если для любой последовательности точек  , сходящейся к  , но не содержащей   в качестве одного из своих элементов (то есть в проколотой окрестности   ), последовательность значений функции   сходится к  .[1]

[править]Предел функции по Коши

Значение   называется пределом (предельным значением) функции   в точке  , если для любого наперёд взятого положительного числа   найдётся отвечающее ему положительное число   такое, что для всех аргументов  , удовлетворяющих условию  , выполняется неравенство  .[1]

16. Односторонние пределы. Бесконечно большие и ограниченные пределы.

Односторонние пределы

Любой интервал (, а), правым концом которого является точка а, называется левой окрестностью точки а.  Аналогично любой интервал (a, ), левым концом которого является точка а, называется ее правой окрестностью.  Символически запись  означает, что х стремится к а справа, оставаясь большим а, то есть при х > а;   означает, что х стремится к а слева, то естьпри х < а. будем называть левосторонним пределом функции при  слева,  -это правосторонний предел функции.  Теорема. Функция у = f(х) имеет   в том и только в том случае, когда существуют и равны друг другу ее   и  . Tогда   =   =

Бесконечно малые и бесконечно большие

Функция  (х) называется бесконечно малой при ха, если   Ясно, что тогда (x)   для x  O (а, б) и   > 0.  Функция f(х) называется бесконечно большой при  если . Это равносильно тому, что каким бы ни было число М > 0, найдется такая окрестность О (а, б), что для всех x  O (а, б)   M.  Лемма. Если f(х)  при х а, то  0 при ха. Если  (x)  0 при x a, то    при x  a и  (x)  0.  Действительно, пусть f(x)  , то есть является бесконечно большой. Тогда f(x)  М для x  O (а, б).   для x  O (а, б), то есть   для x  O (а, б), это означает, что  , так как  можно взять в качестве  > 0.  Аналогично доказывается вторая часть утверждения.

17. Два определения БМВ(бесконечно малая величина).

Бесконечно малая (величина) - числовая функция или последовательность, которая стремится к нулю.

Бесконечно малая величина есть такая переменная величина, предел которой есть 0, или, что то же самое, это есть такая переменная величина, которая может быть сделана менее всякой данной величины. Поэтому Б. м. величину называют также иногда произвольно малою величиной.

1. Если переменная величина xn имеет своим пределом нуль lim xn = 0, то она называется бесконечно малой. Это же определение можно высказать и в другой формулировке:

Переменная величина xn назвается бесконечно малой, если для всякого наперед заданного положительного числа можно указать такое натуральное число N, что | xn | < для всех номеров n, которые больше N.

Ни одно число, кроме нуля, не может быть отнесено к бесконечно малым величинам.

2. Алгебраическая сумма нескольких бесконечно малых величин есть также величина бесконечно малая.

Алгебраической суммой называется такая сумма, члены которой присоединяются друг к другу не только при помощи знака плюс, но и при помощи знака минус.

3. Разность двух бесконечно малых величин есть величина бесконечно малая.

4. Произведение ограниченной переменной величины на бесконечно малую есть величина бесконечно малая.

Отсюда следует:

а) Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.

б) Произведение переменной величины, стремящейся к пределу, на бесконечно малую есть величина бесконечно малая.

в) Произведение двух бесконечно малых величин есть величина бесконечно малая.

5. Отношение двух бесконечно малых величин не обязательно есть величина бесконечно малая.

Отношение двух бесконечно малых величин может быть величиной конечной, бесконечно малой и даже бесконечно большой величиной.

Об отношении двух бесконечно малых величин иногда говорят, что оно представляет собой "неопределенность" вида .

Вычисление предела отношения двух бесконечно малых часто называется также раскрытием "неопределенности" вида .

18. Связь между БМВ(бесконечно малая величина). и ББВ(бесконечно большая величина).

Бесконечно малые и бесконечно большие величины - Бесконечно малая величина есть такая переменная величина, предел которой есть 0, или, что то же самое, это есть такая переменная величина, которая может быть сделана менее всякой данной величины. Поэтому Б. м. величину называют также иногда произвольно малою величиной. Б. большая величина, или произвольно большая величина, напротив, есть такая, которая может быть сделана более всякой данной величины. Эти два вида переменных величин взаимно соответствуют один другому и должны быть рассматриваемы вместе. Так, в элементарной геометрии разность между длиной окружности круга и периметром вписанного или описанного многоугольника с произвольно большим числом сторон есть величина произвольно малая. Б. малые и Б. большие величины делят на различные порядки. Выбирая из данных переменных величин одну какую-нибудь за малую величину первого порядка, называют Б. малыми величинами того же первого порядка всякую Б. малую величину, отношение которой к данной есть величина конечная. Если же отношение это есть Б. малая величина и притом 1-го порядка, то ее называют Б. малой величиной 2 -го порядка и т. д. Таким образом, если, напр., ? есть бесконечно малая величина, а k какая-нибудь конечная величина, то k? есть также Б. малая величина 1-го порядка, а ? n есть Б. малая величина n-го порядка. В то же время 1/? считается Б. большой величиной 1-го порядка, 1/? n - Б. большой величиной n-го порядка и т. д. Порядок малости или великости какой-нибудь переменной величины может быть не только целый, но и дробный, или иррациональный; так, напр., при Б. большом х 1-го порядка величина logx есть Б. большая величина Б. малого порядка. Громадное значение, какое имеют Б. малые величины в анализе, основано на следующих двух положениях: I. При разыскании предела отношения двух выражений, содержащих Б. малые величины различных порядков, можно отбросить все Б. малые величины кроме тех, порядок которых наименьший. II. При разыскании предела суммы выражения, содержащего Б. малые величины различных порядков, можно отбросить все Б. малые величины кроме тех, порядок которых наименьший. На этих положениях основано все дифференциальное и интегральное исчисление (см, это сл.). В течение долгого времени эти свойства Б. малых величин казались парадоксальными и возбуждали споры и возражения со стороны многих математиков.

19. Теорема о структуре сходящихся переменных.

Структура сходящихся последовательностей

Последовательность, у которой существует предел, называется сходящейся.

Последовательность не являющаяся сходящейся называется расходящейся.

Определение: Последовательность {xn} называется сходящейся, если

существует такое число а, что последовательность {xn-а} является

бесконечно малой. При этом число а называется пределом последовательности

{xn}.

В соответствии с этим определением всякая бесконечно малая

последовательность является сходящейся и имеет своим пределом число ноль.

Можно, также, дать еще одно определение сходящейся последовательности:

Последовательность {xn} называется сходящейся, если существует такое число

а, что для любого положительного числа ( можно указать номер N такой, что

при n(N все элементы xn этой последовательности удовлетворяют неравенству:

|xn-a|<(.

При этом число а называется пределом последовательности.

Некоторые свойства сходящихся последовательностей:

ТЕОРЕМА: Сходящаяся последовательность имеет только один предел.

Доказательство: Пусть a и b - пределы сходящейся последовательности

{xn}. Тогда, используя специальное представление для элементов xn

сходящейся последовательности {xn}, получим xn=а+(n, xn=b+(n, где (n и (n -

элементы бесконечно малых последовательностей {(n} и {(n}.

Вычитая данные соотношения, найдем (n-(n=b-a. Так как все элементы

бесконечно малой последовательности {(n-(n} имеют одно и то же постоянное

значение b-a, то (по теореме: Если все элементы бесконечно малой

последовательности {(n} равны одному и тому же числу с, то с=0) b-a=0, т.е.

b=a. Теорема доказана.

ТЕОРЕМА: Сходящаяся последовательность ограничена.

Доказательство: Пусть {xn} - сходящаяся последовательность и а - ее

предел. Представим ее в следующем виде:

xn=а+(n,

где (n- элемент бесконечно малой последовательности. Так как бесконечно

малая последовательность {(n} ограничена (по теореме: Бесконечно малая

последовательность ограничена.), то найдется такое число А, что для всех

номеров n справедливо неравенство |(n|(А. Поэтому | xn | ( |a| + A для всех

номеров n, что и означает ограниченность последовательности {xn}. Теорема

доказана.

Ограниченная последовательность может и не быть сходящейся. Например,

последовательность 1, -1, 1, -1, … - ограничена , но не является

сходящейся. В самом деле, если бы эта последовательность сходилась к

некоторому числу а, то каждая из последовательностей {xn-a} и {xn+1-a}

являлась бы бесконечно малой. Но тогда (по теореме: Разность бесконечно

малых последовательностей есть бесконечно малая последовательность.) {(xn-

a) - (xn+1-a)}={xn- xn+1} была бы бесконечно малой, что невозможно т.к.

|xn- xn+1| = 2 для любого номера n.

ТЕОРЕМА: Сумма сходящихся последовательностей {хn} и {yn} есть

сходящаяся последовательность, предел которой равен сумме пределов

последовательностей {хn} и {yn}.

Доказательство: Пусть а и b - соответственно пределы

последовательностей {хn} и {yn}. Тогда:

xn=а+(n, yn=b+(n,

где {(n} и {(n) - бесконечно малые последовательности. Следовательно, (хn +

yn) - (а + b) =(n+(n.

Таким образом, последовательность {(хn + yn) - (а + b)} бесконечно

малая, и поэтому последователдьность {хn + yn} сходится и имеет своим

пределом число а+b. Теорема доказана.

ТЕОРЕМА: Разность сходящихся последовательностей {хn} и {yn} есть

сходящаяся последовательность, предел которой равен разности пределов

последовательностей {хn} и {yn}.

Доказательство: Пусть а и b - соответственно пределы

последовательностей {хn} и {yn}.Тогда:

xn=а+(n, yn=b+(n,

где {(n} и {(n) - бесконечно малые последовательности. Следовательно, (хn -

yn) - (а - b) =(n-(n.

Таким образом, последовательность {(хn - yn) - (а - b)} бесконечно

малая, и поэтому последователдьность {хn - yn} сходится и имеет своим

пределом число а-b. Теорема доказана.

ТЕОРЕМА: Произведение сходящихся последовательностей {хn} и {yn} есть

сходящаяся последовательность, предел которой равен произведению пределов

последовательностей {хn} и {yn}.

Доказательство: Пусть а и b - соответственно пределы

последовательностей {хn} и {yn}, то xn=а+(n, yn=b+(n и

xn(yn=a(b+a((n+b((n+(n((n. Следовательно,

xn(yn-а(b=a((n+b((n+(n((n.

(в силу теоремы: Произведение ограниченной последовательности на бесконечно

малую есть бесконечно малая последовательность.) последовательность

{a((n+b((n+(n((n} бесконечно малая, и поэтому последовательность {xn(yn-

а(b} тоже бесконечно малая, а значит последовательность {xn(yn} сходится и

имеет своим пределом число а(b. Теорема доказана.

ЛЕММА: Если последовательность {yn} сходится и имеет отличный от ноля

предел b, то, начиная с некоторого номера, определена последовательность

[pic], которая является ограниченной.

Доказательство: Пусть [pic]. Так как b(0, то (>0. Пусть N - номер,

соответствующий этому (, начиная с которого выполняется неравенство:

|yn-b|<( или |yn-b|<[pic]

из этого неравенства следует, что при n(N выполняется неравенство

|yn|>[pic]. Поэтому при n(N имеем [pic]. Следовательно, начиная с этого

номера N, мы можем рассматривать последовательность [pic], и эта

последовательность ограничена. Лемма доказана.

ТЕОРЕМА: Частное двух сходящихся последовательностей {xn} и {yn} при

условии, что предел {yn} отличен от ноля, есть сходящаяся

последовательность, предел которой равен частному пределов

последовательностей {xn} и {yn}.

Доказательство: Из доказанной ранее леммы следует, что, начиная с

некоторого номера N, элементы последовательности {yn} отличны от ноля и

последовательность [pic] ограничена. Начиная с этого номера, мы и будем

рассматривать последовательность [pic]. Пусть а и b - пределы

последовательностей {xn} и {yn}. Докажем, что последовательность [pic]

бесконечно малая. В самом деле, так как xn=а+(n, yn=b+(n, то

[pic][pic].

Так как последовательность [pic] ограничена, а последовательность [pic]

бесконечно мала, то последовательность [pic] бесконечно малая. Теорема

доказана.

Итак, теперь можно сказать, что арифметические операции над сходящимися

последовательностями приводят к таким же арифметическим операциям над их

пределами.

ТЕОРЕМА: Если элементы сходящейся последовательности {xn}, начиная с

некоторого номера, удовлетворяют неравентству xn(b (xn(b), то и предел а

этой последовательности удовлетворяет неравенству а(b (a(b).

Доказательство: Пусть все элементы xn, по крайней мере начиная с

некоторого номера, удовлетворяют неравенству xn(b. Предположим, что а<xn-ab, однако при этом предел а может оказаться равным

b. Например, если xn=1/n, то xn>0, однако [pic].

Следствие 1: Если элементы xn и уn у сходящихся последовательностей

{xn} и {yn}, начиная с некоторого номера, удовлетворяют неравенству xn (

уn, то их пределы удовлетворяют аналогичному неравенству

[pic].

Элементы последовательности {yn-xn} неотрицательны, а поэтому

неотрицателен и ее предел [pic]. Отсюда следует, что

[pic].

Следствие 2: Если все элементы сходящейся последовательности {xn}

находятся на сегменте [a,b], то и ее предел с также находится на этом

сегменте.

Это выполняется, так как а(xn(b, то a(c(b.

ТЕОРЕМА: Пусть {xn} и {zn}- сходящиеся последовательности, имеющие

общий предел а. Пусть, кроме того, начиная с некоторого номера, элементы

последовательности {yn}удовлетворяют неравенствам xn(yn(zn. Тогда

последовательность {yn} сходится и имеет предел а.

Доказательство: достаточно доказать, что {yn-a} является бесконечно

малой. Обозначим через N' номер, начиная с которого, выполняются

неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера,

будут выполнятся также неравенства xn-а ( yn-а ( zn-а. Отсюда следует, что

при n(N' элементы последовательности {yn-a} удовлетворяют неравенству

|yn-a| ( max {|xn-a|, |zn-a|}.

Так как [pic] и [pic], то для любого (>0 можно указать номера N1 и N2

такие, что при n(N1 |xn-a|<(, а при n(N2 |zn-a|<(. Итак

последовательность {yn-a} бесконечно малая. Теорема доказана.

Итак, мы показали неравенства, которым удовлетворяют элементы

сходящихся последовательностей, в пределе переходят в соответствующие

неравенства для пределов этих последовательностей.

20. Теоремы о пределах сходящихся переменных.

 Числовая последовательность может иметь только один предел.

Доказательство. Предположим противное. Это означает, что существует последовательность  , имеющая два различных предела а и в. По лемме   и  , где   и   – бесконечно малые последовательности, откуда получаем  . Так как все элементы бесконечно малой последовательности   имеют одно и по же значение в-а, то в-а=0, то есть в=а, что противоречит предположению. Теорема доказана.

Теорема 8. Сходящаяся числовая последовательность ограничена.

Доказательство. Пусть   – сходящаяся к числу а, тогда  , где  . Так как бесконечно малая последовательность ограничена, то $ такое число  , что для всех   выполняется  . Поэтому   для всех  , а это и означает, что последовательность   ограничена.

Теорема 9. Если последовательность   сходится к числу а, то и любая подпоследовательность этой последовательности сходится к этому же числу.

Доказательство. По условию  , то есть для любого числа   существует такой номер N, что для всех номеров   выполняется неравенство  . Пусть   – некоторая подпоследовательность последовательности  . Тогда для всех номеров   выполняется  , поэтому  .

Замечание. Теорема 3 справедлива для случая  , то есть для бесконечно большой последовательности  . Таким образом, каждая подпоследовательность бесконечно большой последовательности является бесконечно большой последовательностью. Доказательство этого утверждения аналогично доказательству теоремы 3.

Теорема 10. Если последовательность   сходится к числу  , то, начиная с некоторого номера, определена последовательность  , которая является ограниченной.

Доказательство. Пусть  , так как  . Пусть N – номер, начиная с которого выполняется условие  . Отсюда при   получаем   или  . Тогда при    , что означает ограниченность последовательности  , начиная с номера N.

Рассмотрим теперь несколько простейших свойств пределов числовых последовательностей.

1. Если  ,  , с – действительное число, то  .

Доказательство. Последовательность   – бесконечно малая и поэтому по лемме  .

2. Если последовательность сходится, то последовательности   также сходятся, причем  .

Доказательство. Пусть  ,  . По лемме  ,  ,  , где  . Следовательно,  , где по свойству бесконечно малых последовательностей  . Поэтому по лемме получаем  .

Следствие. Свойство 2 выполняется для любого конечного числа сходящихся последовательностей.

3. Если последовательности   и   сходятся, то последовательность   также сходится, причем  .

Доказательство. Пусть  ,  , тогда  ,  ,  , где  , поэтому  . По свойствам бесконечно малых последовательностей   – бесконечно малая. Тогда по лемме  .

Следствие 1. Если последовательность   сходится, то для любого числа с последовательность   также сходится, причем  .

Следствие 2. Если последовательность   сходится и k – натуральное число, то последовательность { } также сходится, причем  .

4. Если последовательности   и   сходятся,   при   и  , то последовательность   также сходится, причем  .

Доказательство. Пусть  ,  , тогда  ,  , где  . По теореме 10 существует номер N такой, что для всех номеров   последовательность   ограничена

 

Последовательность   бесконечно малая при  , так как   – ограничена, а   – бесконечно малая последовательность. Таким образом, теорема доказана.

21. Некоторые приёмы раскрытия неопределённостей.

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов  ,  ,   пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

Для раскрытия неопределённостей типа   используется следующий алгоритм:

Выявление старшей степени переменной;

Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа   существует следующий алгоритм:

Разложение на множители числителя и знаменателя;

Сокращение дроби.

Для раскрытия неопределённостей типа   иногда удобно применить следующее преобразование:

Пусть   и 

[править]Пример

«Замечательный предел»   — пример неопределённости вида  . По правилу Лопиталя

22. Теорема о сжатой переменной.

Теорема о сжатой переменной (о двух милиционерах) - теорема в математическом анализе о существовании предела у функции, которая "зажата" между двумя другими функциями, имеющими одинаковый предел. Формулируется следующим образом:

Если функция y = f(x) такая, что ф(х)<=f(х)<=Ф(х) для всех x в некоторой окрестности точки a, причем функции ф(х) и Ф(х) имеют одинаковый предел при х->а, то существует предел функции y = f(x) при х->а, равный этому же значению, то есть

Лим(ф(х))=лим(Ф(х))=а => лим(f(х))=а

Пусть, начиная с некоторого , выполняются неравенства , причем крайние переменные имеют одинаковый конечный предел , тогда переменная также имеет предел, причем тот же самый.

Доказательство:

Возьм?м любое , по определению предела начиная с некоторого номера будут выполняться неравенства:

и В силу неравенств (*) выполняется неравенство (начиная с некоторого номера ):

Это и означает, что переменная имеет пределом . , ч. т. д.

23. Вывод формулы первого замечательного предела.

Первым замечательным пределом именуют  . Известны также и следствия из первого замечательного предела:

       Все приведенные выше формулы получаются из основной:  . Примечательность последней формулы состоит в том, что вместо х можно подставлять любое выражение, лишь бы это выражение стремилось к нулю.

24. Второй замечательный предел для ЧП и функции.

В теории пределов так называется каждое из трех равенств: , где е = 2,71828… – как доказано в 1873 г. французским математиком Ш. Эрмитом,трансцендентное число(Трансцендентное число – число, которое не является корнем никакого многочлена с целыми коэффициентами. Иначе говоря, трансцендентное число – это число, не являющееся алгебраическим. В зависимости от того, над каким числовым полем рассматриваются многочлены с целыми коэффициентами, областями, над которыми рассматриваются трансцендентные числа, служат полядействительных, комплексных или р-адических чисел.), основание натуральных логарифмов, говорят такженеперово число (названо в честь шотландского математика Непера; как считают многие современные исследователи, необоснованно).

25. Сравнение БМВ, применение эквивалентных БМВ при вычислении пределов.

Зададимся вопросом, как можно сравнить две бесконечно малые величины или две бесконечно большие величины?

Определения. Пусть при   функции f(x) и g(x) являются бесконечно малыми. Тогда:

2. Если   , то f(x) называется бесконечно малой высшего порядка относительно g(x).

2. Если   (конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).

3. Если   , то f(x) и g(x) называются эквивалентными бесконечно малыми.Эквивалентность записывается так:   .

Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак  мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.

26. Два определения непрерывности функции в точке.

Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.

Тот же факт можно записать иначе:

Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 - точкой разрыва.

Функциональные ряды Примеры решения задач математика

Пример непрерывной функции:

y

 f(x0)+

 f(x0)

 f(x0)-

 

0 x0- x0 x0+  x 

Пример разрывной функции:

 

  y

 

 f(x0)+

 f(x0)

 f(x0)-

  x0 x

 

  Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

верно неравенство  .

 

  Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.

 

f(x) = f(x0) + (x)

где (х) – бесконечно малая при хх0.

27. Непрерывность функци на интервале. Точки разрыва функции 1-го и 2-го рода.

Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.

Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.

Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Замечание. Функция, непрерывная на отрезке [a,b] может быть разрывной в точках a и b (рис. 1)

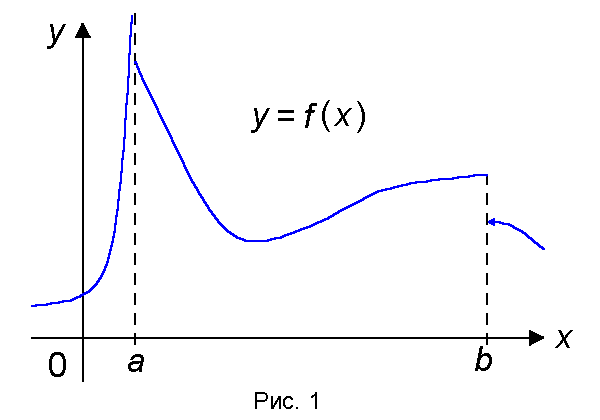
Множество функций, непрерывных на отрезке [a, b] обозначается символом C[a, b].

Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если - значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .

Точки разрыва первого и второго рода

Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:

если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;

если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

28. Свойства непрерывных функций.

в отрезке:

1. Если ф-ция y=f(x) непрерывна на [a,b] и f(a)*f(b)<0, т.е. знаки f(a) и f(b) противоположны, то на (a,b)  найдется хотя бы одна точка х=с, что f(c)=0 (график)-теорема Больцана-Коши.

2. Если ф-ция y=f(x) непрерывна на [a,b], то она ограничена на этом промежутке.

3. Если ф-ция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке min m и max M (теорема Вейерштрасса).

в точке:

1. если ф-ция f(x) и g(x) непрерывна в х0, то их сумма,произведение, частное (при φ(х0)≠0) явл. ф-циями, непрерывными в х0

2. если ф-ция y=f(x) непрерывна в х0, и f(x0)>0, то существует окрестность х0, в которой f(x)>0

3. если y=f(U) непрерывна в U0, а U=φ(x) непрерывна в U0=φ(x0), то сложная ф-ция y=f[φ(x)] непрерывна в х0.

Локальные

Функция, непрерывная в точке  , является ограниченной в некоторой окрестности этой точки.

Если функция   непрерывна в точке   и   (или  ), то   (или  ) для всех  , достаточно близких к  .

Если функции   и   непрерывны в точке  , то функции   и   тоже непрерывны в точке  .

Если функции   и   непрерывны в точке   и при этом  , то функция   тоже непрерывна в точке  .

Если функция   непрерывна в точке   и функция   непрерывна в точке  , то их композиция   непрерывна в точке  .

[править]Глобальные

Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.

Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.

Областью значений функции  , непрерывной на отрезке  , является отрезок   где минимум и максимум берутся по отрезку  .

Если функция   непрерывна на отрезке   и   то существует точка   в которой  .

Если функция   непрерывна на отрезке   и число   удовлетворяет неравенству   или неравенству   то существует точка   в которой  .

Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.

Монотонная функция на отрезке   непрерывна в том и только в том случае, когда область ее значений является отрезком с концами   и  .

Если функции   и   непрерывны на отрезке  , причем   и   то существует точка   в которой   Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.