
1. Понятие матрица. Действие над матрицами.
Определение. Матрицей размера m n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМО-УГОЛЬНАЯ ИЛИ КВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ.
ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ,НАЗЫВАЮТСЯ ЭЛЕМЕНТАМИ МАТРИЦЫ.
Операции над матрицыми.
1. ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
2. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
-Исходная матрица 3х2
-Транспонированная матрица 2х3
3.МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО
СКЛАДЫВАТЬ И ВЫЧИТАТЬ
4.Умножение строки на столбец (скалярное произведение)
5.Умножение матрица на столбец (кажая строка матрицы скалярно умножается на столбец)
6.ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ
МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА
МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B
7.Умножение матрицы на матрицу
КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ
8.УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование
2. Определитель. Вычисление определителей.
Определи?тель (или детермина?нт) - одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.Определитель матрицы А обозначается как: det(A), |А| или ?(A).
Пусть A = (aij) (i, j = 1, …, n) - квадратная матрица порядка n. Определителем (или детерминантом) матрицы A называется число, которое ставится в соответствие этой матрице и может быть вычислено по ее элементам. Обозначается определитель матрицы A символами
Определитель матрицы n?n называется определителем n-го порядка.
Правило вычисления определителей
1. Определителем матрицы 1?1, состоящей из одного числа, будем считать само это число.
2. Определитель матрицы 2?2 вычисляется по формуле
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка . Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы будем обозначать или det .
Определение 1. Определителем квадратной матрицы второго порядка называется число .
Определителем квадратной матрицы порядка , , называется число
где - определитель матрицы порядка , полученной из матрицы вычеркиванием первой строки и столбца с номером .
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка:
Замечание. Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание. В определении 1 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Замечание. В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение det .
Рассмотрим некоторые свойства определителей, которые сформулируем в виде утверждений.
Утверждение 1. При транспонировании матрицы определитель не меняется, то есть .
Утверждение 2. Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть .
Утверждение 3. Если в матрице поменять местами две строки, то ее определитель сменит знак.
Утверждение 4. Если матрица имеет две одинаковые строки, то ее определитель равен нулю.
В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Утверждение 5. Если строку матрицы умножить на число , то ее определитель умножится на это число.
Утверждение 6. Если матрица содержит нулевую строку, то ее определитель равен нулю.
Утверждение 7. Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
Утверждение 8. Пусть в матрице i-ая строка имеет вид . Тогда , где матрица получается из матрицы заменой i-ой строки на строку , а матрица - заменой i-ой строки на строку .
Утверждение 9. Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Утверждение 10. Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
3. Свойства определителей.
Определитель - кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , где и т. д. - строчки матрицы, - определитель такой матрицы.
При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
С использованием индексной нотации определитель матрицы 3?3 может быть определён с помощью символа Леви-Чивита из соотношения:
Определитель транспонированной матрицы равен определителю исходной матрицы:
![]()
Это свойство вытекает из определения детерминанта и выражает равноправие строк и столбцов определителя.
Умножение всех элементов строки или столбца определителя на некоторое число λ равносильно умножееию определителя на это число:
![]() .
.
Такое свойство определителей позволяет, в частности, выносить общий множитель элементов строки или столбца за знак определителя.
Если в определителе переставить местами любые две строки или два столбца, то определитель изменяет свой знак на противоположный.
 .
.
Если матрица содержит нулевую строку (столбец), то определитель этой матрицы равен нулю:
![]() .
.
Если две строки (столбца) матрицы равны между собой, то определитель этой матрицы равен нулю:
![]() .
.
Если две строки (столбца) матрицы пропорциональны друг другу, то определитель этой матрицы равен нулю:
 .
.
Епределитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:
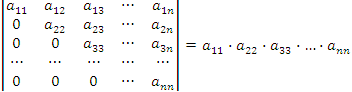 .
.
Если все элементы k-ой строки (столбца) определителя представлены в виде сумм ak j + bk j, то определитель можно представить в виде суммы соответствующих определителей:
![]()
![]() .
.
ЕОпределитель не изменится, если к элементам любой его строки (или столбца) прибавить соответствующие элементы другой строки (или соответствующего столбца), умноженные на одно и тоже число:
![]()
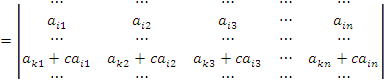
Пусть A и B – квадратные матрицы одного и того же порядка. Тогда определитель произведения матриц равен произведению определителей:
![]()
4. Т. Крамера и её формулы.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
? = det (ai j)
и n вспомогательных определителей ? i (i= ), которые получаются из определителя ? заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
? ? x i = ? i ( i = ). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i = ? i / ?.
Если главный определитель системы ? и все вспомогательные определители ? i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы ? = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
5. Метод Гаусса, решение системы линейных ур-ний.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными
Расширенная матрица этой системы имеет вид
Метод Гаусса основывается на следующих утверждениях.
I. Системы уравнений, полученные в результате следующих преобразований:
перестановка уравнений;
умножение уравнения на любое число. отличное от нуля;
прибавление одногоуравнения, умноженного на любое число, к другому уравнению,
являются эквивалентными, т.е. имеют одни и те же решения.
II. Преобразованиям уравнений системы, очевидно, соответствуют элементарные преобразования строк расширенной матрицы системы:
перестановка строк;
умножение всех элементов строки на любое число. отличное от нуля;
прибавление элементов одной строки, умноженных на одно и то же число, к соответствующим элементам другой строки.
Матрицы A и B, полученные одна из другой с помощью элементарных преобразований строк, называются эквивалентными, что обозначается A ? B.
Чтобы решить систему n уравнений с n неизвестными, нужно расширенную матрицу системы с помощью элементарных преобразований строк привести к такому виду, чтобы основная матрица системы (стоящая слева от черты)
Метод Гаусса является наиболее широко распространенным методом решения задач линейной алгебры; как вы увидите в дальнейшем, с его помощью решаются самые разные задачи.
Дана система линейных алгебраических уравнений (СЛАУ) с неизвестными. Требуется решить эту систему: определить, сколько решений она имеет (ни одного, одно или бесконечно много), а если она имеет хотя бы одно решение, то найти любое из них.
Формально задача ставится следующим образом: решить систему:
где коэффициенты и известны, а переменные - искомые неизвестные.
Удобно матричное представление этой задачи:
где - матрица , составленная из коэффициентов , и - векторы-столбцы высоты .
Стоит отметить, что СЛАУ может быть не над полем действительных чисел, а над полем по модулю какого-либо числа , т.е.:
- алгоритм Гаусса работает и для таких систем тоже (но этот случай будет рассмотрен ниже в отдельном разделе).
