
- •2. Вероятности случайных событий (теоремы сложения и умножения вероятностей)
- •3. Формула Бернулли
- •4. Функция распределения случайных величин и ее свойства
- •5. Дискретные случайные величины и их числовые характеристики
- •6. Плотность вероятности случайных величин и ее свойства (равномерный и нормальный законы распределения)
- •7. Непрерывные случайные величины и их числовые характеристики
- •1. Равномерная случайная величина.
- •8. Дискретные случайные векторы и их числовые характеристики (теорема сложения дисперсий)
- •9. Непрерывные случайные векторы и их числовые характеристики
- •10. Независимость и некоррелированность случайных величин, связь между ними
- •11. Точечные оценки неизвестных параметров распределений (выборочные среднее и дисперсия) Точечные оценки. Методы нахождения точечных оценок
- •12. Интервальные оценки неизвестных параметров распределений (математического ожидания и дисперсии нормальнораспределенной генеральной совокупности)
9. Непрерывные случайные векторы и их числовые характеристики
 .
(3.5)
.
(3.5)




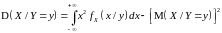
10. Независимость и некоррелированность случайных величин, связь между ними
Случайные величины
и
называются независимыми,
если для любых
 имеет место равенство:
имеет место равенство:

или, в терминах функций распределения,
 .
(3.9)
.
(3.9)
Случайные величины
и
,
для которых корреляционный момент
 ,
называются некоррелированными.
,
называются некоррелированными.
из независимости случайных величин всегда следует их некоррелированность
Безразмерным аналогом является коэффициент корреляции, определяемый формулой:
 ,
,
11. Точечные оценки неизвестных параметров распределений (выборочные среднее и дисперсия) Точечные оценки. Методы нахождения точечных оценок
При k
= 1 величину
 называют выборочным
средним
и обозначают
называют выборочным
средним
и обозначают
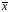 :
:

При
 величину
величину
 называют
выборочной
дисперсией
и
обозначают
называют
выборочной
дисперсией
и
обозначают
 :
:
 .
.
При
точечном оценивании ищут статистику
 ,
(т.е. функцию, зависящую только от выборки
,
(т.е. функцию, зависящую только от выборки
 ),
значение которой при заданной выборке
принимают за приближенное значение
параметра
),
значение которой при заданной выборке
принимают за приближенное значение
параметра
 .
В этом случае статистику
называют оценкой
параметра
.
.
В этом случае статистику
называют оценкой
параметра
.
Обосновать
качество оценки
 можно лишь исходя из ее свойств, не
зависящих от конкретной выборки. Для
изучения таких свойств (естественно,
вероятностного характера) в соответствии
с замечанием из п. 1.1. под оценкой следует
понимать случайную
величину
можно лишь исходя из ее свойств, не
зависящих от конкретной выборки. Для
изучения таких свойств (естественно,
вероятностного характера) в соответствии
с замечанием из п. 1.1. под оценкой следует
понимать случайную
величину
 .
Выбор из множества оценок одного и того
же параметра наилучшей основан на
критерии сравнения качества оценок,
предложенном Р.А.Фишером. Согласно этому
критерию оценка
должна быть:
.
Выбор из множества оценок одного и того
же параметра наилучшей основан на
критерии сравнения качества оценок,
предложенном Р.А.Фишером. Согласно этому
критерию оценка
должна быть:
состоятельной, т. е. с возрастанием объема выборки
 должна сходиться по вероятности к
истинному неизвестному значению
параметра
:
должна сходиться по вероятности к
истинному неизвестному значению
параметра
:
 ;
;несмещенной, т. е. математическое ожидание должно быть равно оцениваемому параметру :
 ;
;
эффективной, т. е. должна обладать минимальной дисперсией в рассматриваемом классе оценок.
Величина
 называется смещением
оценки
.
Таким образом, оценка
является
несмещенной тогда и только тогда, когда
ее смещение
называется смещением
оценки
.
Таким образом, оценка
является
несмещенной тогда и только тогда, когда
ее смещение
 .
Оценка
,
у которой
.
Оценка
,
у которой
 при
при
 ,
называется асимптотически
несмещенной.
,
называется асимптотически
несмещенной.
Достаточным условием состоятельности несмещенной оценки в силу неравенства Чебышева является стремление к нулю ее дисперсии:
 при
.
при
.
Эффективность оценки позволяет исследовать следующее неравенство Рао-Крамера: для широкого класса непрерывных распределений и для любой несмещенной оценки , имеющей конечную дисперсию, справедливо неравенство:
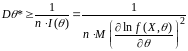 ,
,
где
 - плотность вероятностей наблюдаемой
случайной величины
- плотность вероятностей наблюдаемой
случайной величины
 ,
,
 - информация Фишера о параметре
,
содержащаяся в одном наблюдении над
случайной величиной
.
- информация Фишера о параметре
,
содержащаяся в одном наблюдении над
случайной величиной
.
Таким
образом, оценка
является эффективной, если она обращает
неравенство Рао-Крамера в равенство,
т.е.
 .
.
Наиболее распространенными методами получения точечных оценок неизвестных параметров распределений, удовлетворяющих требованиям 1 - 3 (хотя бы частично), являются метод моментов и метод максимального правдоподобия.
Метод
моментов.
Пусть
- выборка из генеральной совокупности,
имеющей функцию распределения
 ,
зависящую от векторного параметра
,
зависящую от векторного параметра
 .
Предположим, что у наблюдаемой случайной
величины
существуют первые
.
Предположим, что у наблюдаемой случайной
величины
существуют первые
 моментов
моментов
 которые являются функциями от
:
которые являются функциями от
:
 .
Метод моментов состоит в нахождении
решения
.
Метод моментов состоит в нахождении
решения
 системы уравнений, получаемой
приравниванием теоретических моментов
соответствующим выборочным моментам:
системы уравнений, получаемой
приравниванием теоретических моментов
соответствующим выборочным моментам:
 .
.
Для нахождения оценки может быть использована также система уравнений, основанных на приравнивании центральных теоретических и выборочных моментов:
 .
.
Использование именно первых r моментов является необязательным.
В случае двумерного
неизвестного параметра
 его оценка по методу моментов
его оценка по методу моментов
 обычно определяется как решение системы
уравнений:
обычно определяется как решение системы
уравнений:

Оценки, получаемые по методу моментов являются:
- состоятельными (при весьма общих предположениях);
- несмещенными не всегда;
- вообще говоря, неэффективными.
На практике оценки, получаемые по методу моментов, часто используются как первое приближение, на основе которого находятся более «хорошие» оценки.
Достоинство метода моментов заключается в том, что системы уравнений для нахождения оценок решаются довольно просто. Однако имеет место произвол в выборе уравнений для нахождения оценок и метод вообще неприменим, когда моментов необходимого порядка не существует (пример, - закон распределения Коши).
