2.1. Последовательный поиск

При последовательном поиске мы всегда будем предполагать, что список неотсортирован. Перед алгоритмом поиска стоит задача определения местонахождения ключа. Алгоритмы поиска возвращают индекс записи, содержащей нужный ключ. Если ключевое значение не найдено, то алгоритм поиска обычно возвращает значение индекса, превышающее верхнюю границу массива, или нулевое значение.

Для наших целей будем предполагать, что элементы списка имеют номера от 1 до N. Если целевой элемент отсутствует, то возвращаем значение 0. Для простоты предполагаем, что ключевые значения не повторяются.

Алгоритм последовательного поиска последовательно просматривает по одному элементу списка, начиная с первого, до тех пор, пока не найдет целевой элемент.

Пример алгоритма последовательного поиска

SeqSearch (list, target, N)

// list - список для просмотра

// target - цель поиска

// N - число элементов списка

for i = 1 to N do

if list [i][ = target

then return (i)

endif

end for

return 0

end

Значимой операцией в данном алгоритме является операция сравнения.

Лучший случай - целевой элемент стоит первым в списке. Число операций f_А ^(N) =1.

Худший случай - их два. В первом случае целевой элемент стоит в конце списка; во втором - его вообще нет.

В первом случае число сравнений f_А ^(N) = N. Столько же сравнений и во втором случае. Ясно, что N дает верхнюю оценку сложности любого алгоритма поиска, поскольку, если число сравнений больше N, то это означает, что сравнение с каким-то элементом выполнялось дважды.

Анализ среднего случая.

Если целевое значение содержится в списке, то оно может занимать одно из N возможных равновероятных положений, то есть вероятность каждого из них 1/N.

Число сравнений, требующихся для поиска, определяется номером элемента (для первой позиции одно, для второй позиции два и т.д.), следовательно, f_А (N) =  i = =

Последовательный поиск можно применять и на отсортированном списке

Задание: написать алгоритм поиска, выдающего тот же результат, что и предыдущий алгоритм, однако работающий быстрее за счет того, что он останавливается, когда целевое значение оказывается меньше текущего значения в списке.

Использовать функцию

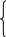-1, если x < y

Compare (x,y) = 0, если x = y

1, если x < y

Вызов функции считать за одно сравнение. Провести анализ в наихудшем случае при условии, что целевое значение найдено.

2.2. Двоичный поиск

При сравнении целевого значения со средним элементом отсортированного списка возможен один из трех исходов: значения равны, целевое значение меньше элемента списка, либо целевое значение больше элемента списка.

В первом и наилучшем случае, поиск завершен. В остальных двух случаях мы можем отбросить сразу половину списка.

Когда целевое значение меньше среднего элемента, мы знаем, что если оно имеется в списке, то находится перед этим средним элементом. Когда же оно больше среднего элемента, то, если оно находится в списке, то стоит после этого среднего элемента. Таким образом, за одно сравнение исключается половина рассматриваемой на данном шаге части списка.

BinarySearch (list, target, N)

start  1

end  N

while start  end do

middle  (start-end) / 2

select (Compare (list (middle, target) from

case - 1: start  middle +1

case 0: return (middle)

case 1: end  middle – 1

end select

end while

return (0)

end

Здесь Start и End – начальный и конечный индекс очередной части списка, middle – ее середина. Start  middle + 1 и end  middle – 1, объясняются тем, что в результате сравнения мы знаем, что среднее значение не является искомым и поэтому его можно исключить из рассмотрения.

Поскольку алгоритм всякий раз делит список пополам, то будем считать, что N=2^k-1 для некоторого k.

Если в некотором проходе цикл имеет дело со списком из 2^j-1 элементов, то в первой половине списка 2^j-1 – 1 элементов, один элемент в середине и 2^j-1 – 1 элементов во второй половине списка. Поэтому к следующему проходу остается 2^j-1 – 1 элемент.

Это предположение позволит упростить анализ, но не является важным.

Анализ наихудшего случая.

Степень двойки в длине оставшейся части списка при всяком проходе цикла уменьшается на 1. Последняя итерация цикла проводится, когда размер оставшейся части становится равным 1, а это происходит, когда j=1 (2^j-1–1 = 1).

Значит, при N=2^k-1 число проходов не превышает k.

Решая это уравнение относительно k, получаем 2^k = N + 1. Следовательно k = log₂ (N + 1) – оценка наихудшего случая, то есть f_А ^(N) = log₂ (N + 1).

Анализ среднего случая.

При анализе среднего случая рассмотрим только вариант, когда целевое значение есть в списке.

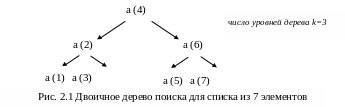
В этом случае у целевого значения N возможных положений. Будем считать, что они равноправны, то есть вероятность каждого из них тем самым равна 1/N. Для вывода формулы рассмотрим двоичное (бинарное) дерево поиска.

Для списка из 2^k – 1 = 7 элементов (k=3) двоичное дерево приведено на рис. 2.1.

Для поиска элемента уровня 1 требуется 1 сравнение; уровня 2 – 2 сравнения. Следовательно, на уровне i требуется i сравнений.

На уровне i содержится (2 i – 1) элементов (узлов). Следовательно, полное число сравнений для всех возможных случаев можно подсчитать, просуммировав произведение числа узлов на каждом уровне на число сравне­ний на этом уровне:  f_А (N) = для N = 2^k-1.

 f_А (N) = =

Так как N=2^k – 1, то 2^k = N + 1, то  f_А (N) =

При росте N значение k/N становится близким к нулю и тогда

 f_А (N)  k – 1  log₂ (N + 1) – 1

Задание. Построить дерево двоичного поиска для N  2^k – 1, например, для N = 10.

Оценить число уровней и узлов на каждом уровне.