1.4. Классификация алгоритмов по виду функции трудоемкости

В зависимости от влияния исходных данных на функцию трудоемкости алгоритма может быть предложена следующая классификация, имеющая практическое значение для анализа алгоритмов:

1. Количественно-зависимые по трудоемкости алгоритмы

Это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:

f_А (D) = f_А (|D|) = f_А (N)

Примерами алгоритмов с количественно-зависимой функцией трудоемкости могут служить алгоритмы для стандартных операций с массивами и матрицами – умножение матриц, умножение матрицы на вектор и т.д.

2. Параметрически-зависимые по трудоемкости алгоритмы

Это алгоритмы, трудоемкость которых определяется не размерностью входа (как правило, для этой группы размерность входа обычно фиксирована), а конкретными значениями обрабатываемых слов памяти:

f_А (D) = f_А (d₁,…,d_n) = f_А (P₁,…,P_m), m  n

Примерами алгоритмов с параметрически-зависимой трудоемкостью являются алгоритмы вычисления стандартных функций с заданной точностью путем вычисления соответствующих степенных рядов. Очевидно, что такие алгоритмы, имея на входе два числовых значения – аргумент функции и точность, выполняют существенно зависящее от значений количество операций.

а) Вычисление x^k последовательным умножением  f_А (x, k) = f_А (k).

б) Вычисление e^x=(xⁿ/n!), с точностью до   f_А = f_А (x, )

3. Количественно-параметрические по трудоемкости алгоритмы

Однако в большинстве практических случаев функция трудоемкости зависит как от количества данных на входе, так и от значений входных данных, в этом случае:

f_А (D) = f_А (|D|, P₁,…,P_m) = f_А (N, P₁,…,P_m)

В качестве примера можно привести алгоритмы численных методов, в которых параметрически-зависимый внешний цикл по точности включает в себя количественно-зависимый фрагмент по размерности.

3.1 Порядково-зависимые по трудоемкости алгоритмы

Среди разнообразия параметрически-зависимых алгоритмов выделим еще одну группу, для которой количество операций зависит от порядка расположения исходных объектов.

Пусть множество D состоит из элементов (d₁,…,d_n), и |D|=N,

Определим D_p = {(d₁,…,d_n)} как множество всех упорядоченных N-ок из d₁,…,d_n, отметим, что |D_p|=n!.

Если f_А (_iD_p)  f_А (_jD_p), где _iD_p, _jD_p  D_p, то алгоритм будем называть поряд­ково-зависимым по трудоемкости.

Примерами таких алгоритмов могут служить ряд алгоритмов сортировки, алгоритмы поиска минимума и максимума в массиве.

1.5. Классификация скоростей роста. Асимптотический анализ функций

Как было отмечено выше, точное знание количества операций, выполненных алгоритмом, не играет существенной роли в анализе алгоритма для больших размерностей входа. Куда более важной оказывается скорость роста этого количества при возрастании объема входных данных. Она называется скоростью роста функции трудоемкости алгоритма.

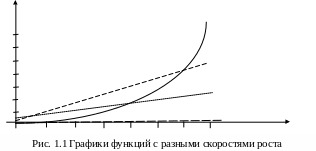
На рис. 1.1 приведено несколько графиков различных функций.

у

х²/8

160

140

120

100 3х

80

60

_{40 х+10}

20

2log x

2 6 10 14 18 22 26 30 х

Значение функции зависит от того, большие или малые значения аргумента мы рассматриваем.

Например, в точке x = 2, наименьшее значение y функции x²/8, а максимальное – у функции (х+10). Однако с ростом х функция x²/8 становится и остается впоследствии наибольшей.

В таблице 1 приведены некоторые часто встречающиеся классы функций (и, соответствующие классы скорости роста).

Таблица 1. Классы скорости роста функций

n	log2 n	n		n log2 n	n2	n3	2n	n!
1 2 5 10 15 20 30 40	0 1.0 2.3 3.3 3.9 4.3 4.9 5.3	1 2 5 10 15 20 30 40	1 1.4 2.23 3.16 3.87 4.47 5.47 6.32	0 2.0 11.6 33.2 58.6 86.4 147.2 212.9	1 4 25 100 225 400 900 1600	1 8 125 1000 3375 8000 27000 64000	2 4 32 1024 32768 1048576 1073741824	1 2 120 3628800 1307674368000 ………………….

Из таблицы видно, что при небольших размерах входных данных значения функций отличаются незначительно, однако при росте этих размеров разница существенно возрастает. На малых объемах принципиальная разница оказывается скрытой, поэтому и проводят сравнения для больших объемов.

Данные рисунка и таблицы иллюстрируют еще одно свойство функций: быстро­растущие функции доминируют функции с более медленным ростом.

Если мы обнаружим, что сложность алгоритма представляет собой сумму двух или несколько функций, то часто отбрасывают все функции, кроме тех, которые растут быстрее всего.

Например, если установлено при анализе алгоритма, что он делает x³ + 30x операций, то говорят, что сложность алгоритма растет как x³. Причина этого в том, что уже при х=100, разница между х³ и (х³+30х) составляет всего лишь 0,3%.

Таким образом, при анализе алгоритма рассматривается общий характер поведения алгоритма, а не подробности этого поведения. Нас, скорее, будет интересовать класс скорости роста, к которому относится алгоритм, нежели точное количество выполняемых операций каждого типа.

При анализе поведения функции трудоемкости алгоритма часто используют принятые в математике асимптотические обозначения, позволяющие показать скорость роста функции, маскируя при этом конкретные коэффициенты.

Такая оценка функции трудоемкости алгоритма называется сложностью алгоритма и позволяет определить предпочтения в использовании того или иного алгоритма для больших значений размерности исходных данных.

В асимптотическом анализе приняты следующие обозначения [1]: