Тема 4 Симплекс – метод

1 Идея симплекс – метода

2 Преобразованная задача

3 Способ перехода от одного ДБР к другому

4 Условие оптимальности ДБР

5 Схема симплекс - метода

6 Сходимость СМ

1. Идея симплекс – метода

[Калихман с.193]

Согласно фундаментальной теореме вместо исследования бесконечного множества ДР, необходимо рассмотреть лишь конечное число ДБР. Таким образом, принципиальная схема решения ЗЛП такова:

1. Найти все ДБР.

2. Вычислить для каждого из них соответствующее значение ЦФ Z.

3. Сравнить и определить наилучшее.

НО!!!!

Но, в общем случае при больших значениях и m количество БР (и, значит и ДБР) может быть огромным (порядка ) и практическое осуществление перебора всех ДБР станет невозможным.

Эти трудности обусловлены тем, что указанная принципиальная схема связана с беспорядочным перебором ДБР, без учета, насколько новое проверяемое ДБР изменяет ЦФ Z и приближает ли оно нас к искомому оптимуму.

Число анализируемых ДБР можно резко сократить, если их перебор производить целенаправленно, добиваясь монотонного изменения ЦФ, т.е. чтобы каждое следующее ДБР было лучше предыдущего (или по крайней мере не хуже).

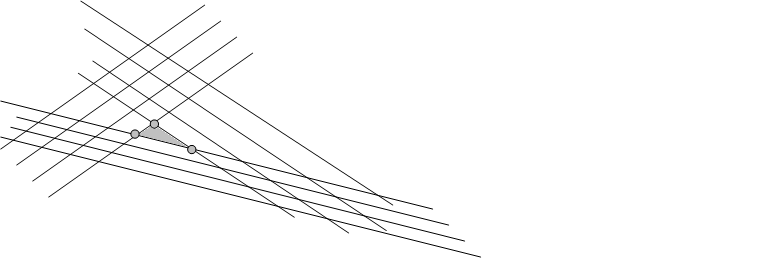
Проиллюстрируем сказанное на рисунке.

Даже если начнем с худшего ДБР, то при целенаправленном переборе (обеспечивающем монотонное улучшение ЦФ) перебор сильно сокращается.

Основной метод решения ЗЛП – симплекс – метод - базируется на идее последовательного улучшения решения.Очевидно, что для реализации этой идеи метод должен включать три основных элемента:

1. Способ определения исходного ДБР.

2. Критерий, по которому можно определить оптимальность найденного решения или необходимость его дальнейшего улучшения.

3. Правило перехода к следующему “лучшему” ДБР.

2 Преобразованная задача (!!!)

Рассмотрим ЗЛП в канонической форме:

(1)

(2)

(3)

• Пусть нам известно, что некоторый вектор х – ДБР системы (2).

Не теряя общности, предположим, что первые столбцов матрицы образуют базис данного ДБР.

Матрицу, составленную из векторов – столбцов, принадлежащих базису, мы условились называть базисной матрицей, по определению – базисная матрица невырожденна.

Пусть

- базисная матрица ДБР (первые столбцов матрицы ).

– матрица, составленная из остальных столбцов матрицы .

Тогда

(4)

В соответствии с представлением (4) разобьем вектор на подвекторы и , т.е.

(5)

Переменные , соответствующие столбцам, вошедшим в базис, мы условились называть базисными переменными. Остальные переменные – небазисными.

где

• – вектор базисных переменных,

• – вектор небазисных переменных.

С учетом (4( и (5) систему (2) можно записать в виде:

(6)

Так как матрица невырожденна, то она имеет обратную матрицу . Домножим (6) слева на .

(7)

Система (7) эквивалентна системе (6), а, следовательно, и системе (2) .

?? Что означает эквивалентна??

• Разобьем вектор с на подвекторы 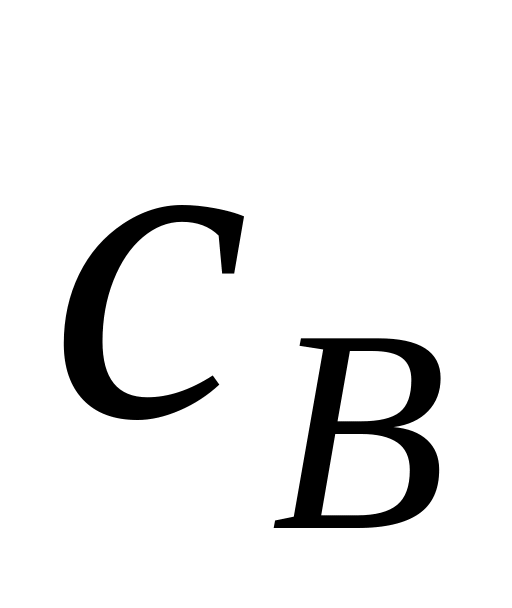и 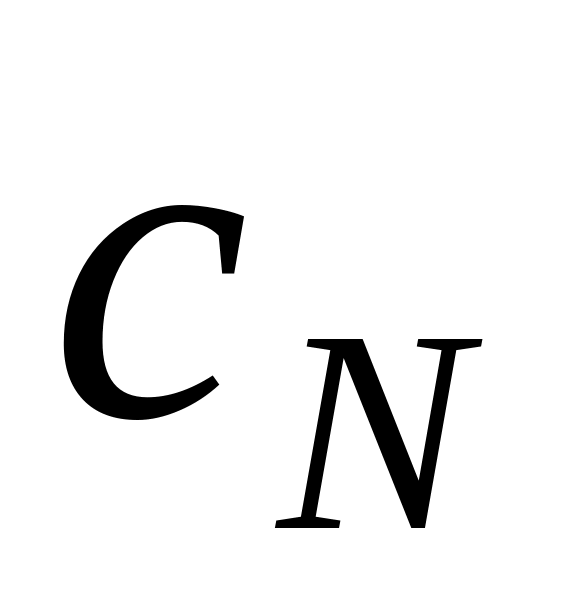, в соответствии с разбиением матрицы А: .

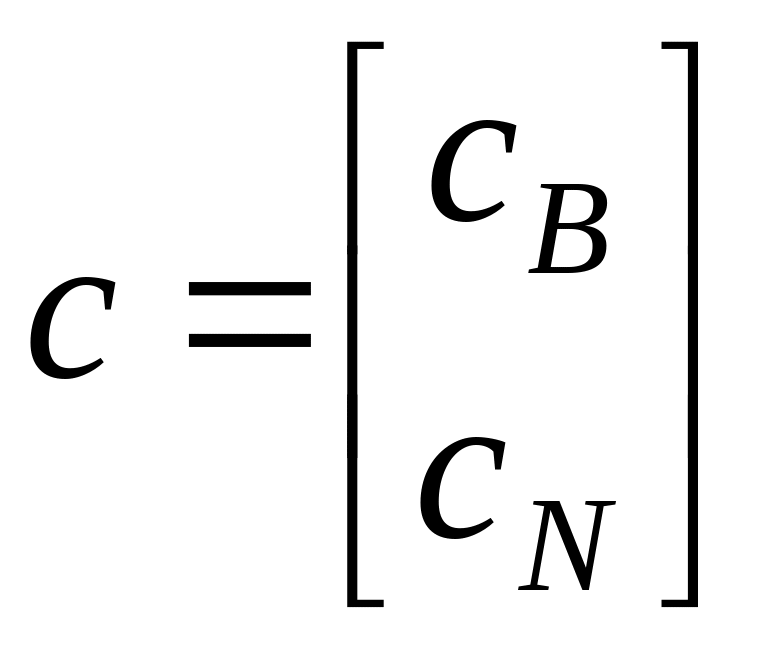Тогда задачу (1) –(3) можно записать в виде:

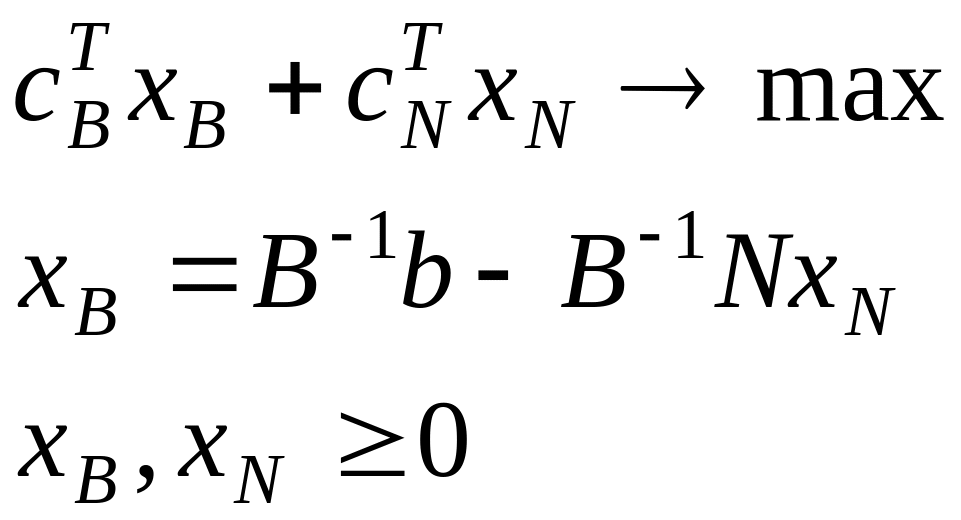
Подставим значение в ЦФ задачи:

Тогда исходная задача может быть представлена в виде:

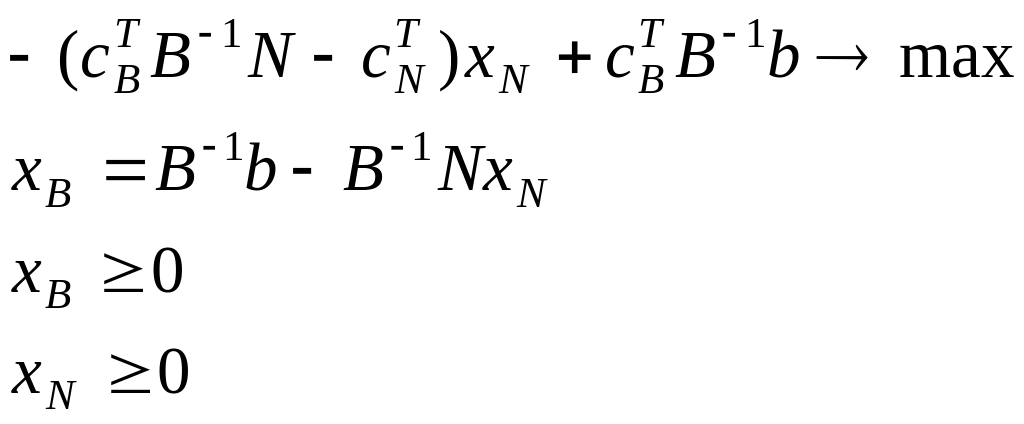
Получили так называемую преобразованную задачу. Обозначим

Можно записать преобразованную задачу следующим образом:

(8)

(9)

(10)

Задача (8)-(10) эквивалентна задаче (1)-(3).

Если же мы положим , то получим (конкретную) точку.

Так как - ДБР, то у него , значит, принимает числовое значение . Т.о. ДБР , а соответствующее значение ЦФ = .

Не смотря на то, что , в преобразованную задачу включаются все компоненты, соответствующие , т.к. они указывают на то, что произойдет со значениями ЦФ и , если один из элементов вектора увеличивается, начиная с нуля.

Иногда задачу (8)-(10) называют диагональной формой исходной задачи, соответствующей ДБР х, а система (9) называется диагональной системой относительно переменных Система названа диагональной, потому что представима в виде:

…