Вопросы для самоконтроля

1. Угол поворота твердого тела, вращающегося вокруг неподвижной оси, меняется со временем по закону где – положительная постоянная. Угловое ускорение равно:

а) б)

в) г)

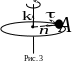
2. Твердое тело начинает вращаться вокруг неподвижной оси. Направление вращения показано на рис. 3. Вектор полного ускорения некоторой точки тела, отстоящей от оси вращения на расстоянии изменяется со временем по закону где – положительная постоянная, и – единичные векторы, жестко связанные с точкой , направления которых показаны на рис. 3. Укажите правильные равенства:

а) б) в)

г) д) е)

где и – векторы угловой скорости и углового ускорения точки , – единичный вектор, направленный вдоль оси вращения.

3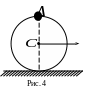 . Колесо радиуса катится без проскальзывания по горизонтальной плоскости. Угловая скорость вращения колеса относительно оси, проходящей через точку равна . Чему равна угловая скорость колеса относительно оси, проходящей через точку (см. рис. 4):

а) б)

в) г) ,

где – скорость центра колеса.

4. Твердое тело совершает плоское движение. Известны направления скоростей двух точек и тела в некоторый момент времени. Какая из точек , , или (см. рис. 5) лежит на мгновенной оси вращения.

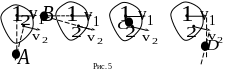
Примеры решения задач

Пример 1. Твердое тело вращается вокруг неподвижной оси по закону , где и – положительные постоянные. Найти:

а) зависимости угловой скорости и углового ускорения от времени;

б) угловое ускорение в момент остановки;

в) средние значения угловой скорости и углового ускорения за промежуток времени от до остановки.

Р е ш е н и е. а) Используя определения угловой скорости и углового ускорения, найдем

, (5)

. (6)

б) Найдем угловое ускорение в момент остановки В этот момент времени угловая скорость будет равна нулю. Из уравнения (5) следует, что

.

Подставляя это значение в (6), получим

.

в) Средней угловой скоростью называется отношение угла поворота тела ко времени , за которое произошел этот поворот

.

Аналогично, среднее угловое ускорение равно:

,

где – изменение угловой скорости за время . Таким образом, для тог чтобы найти значение средней скорости за время движения , надо найти угол, на который повернется твердое тело за это время. Подставляя в уравнение зависимости угла поворота от времени , найдем угол поворота тела к моменту остановки

.

Так как в начальный момент времени угол , получаем

.

Для определения среднего значения углового ускорения, найдем изменение угловой скорости за это время. Так как в начальный момент (см. (5)), а в конечный , получаем

.

Пример 2. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением , где – положительная постоянная. Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол с ее вектором скорости .

Р е ш е н и е. При вращении твердого тела вокруг неподвижной оси все

точки тела движутся по окружностям. Вектор скорости произвольной

точки А тела будет направлен по касательной к окружности, вдоль которой движется эта точка рис 3.

П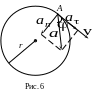 олное ускорение точки А равно

,

где и – тангенциальное и нормальное ускорения соответственно. Направление ускорений показано на рис. 6. Видно, что угол между вектором полного ускорения и вектором скорости – это угол между вектором полного и тангенциального ускорений. Как видно из рисунка,

. (7)

Найдем зависимость угловой скорости от времени. По условию задачи , тогда

.

Разделив переменные

и интегрируя правую и левую части этого уравнения, с учетом того, что в начальный момент времени угловая скорость равна нулю

,

получим зависимость угловой скорости от времени

.

Подставляя в уравнение (7) зависимости угловой скорости и углового ускорения от времени, получим

,

откуда

.

Пример 3. Твердое тело вращается с постоянной угловой скоростью вокруг горизонтальной оси . В некоторый момент времени ось начали поворачивать вокруг вертикальной оси с постоянным угловым ускорением . Найти зависимости угловой скорости и углового ускорения тела от времени.

Р е ш е н и е. В данной задаче твердое тело совершает сложное движение – одновременное вращение вокруг двух взаимно перпендикулярных осей. Пусть направления вращения будут такими, как показано на рис. 7. Вокруг оси тело вращается с постоянной по величине угловой скоростью . Величина угловой скорости вокруг оси меняется со временем по закону

,

т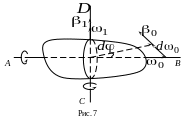 .к. по условию задачи начальная скорость вокруг этой оси равна нулю

и угловое ускорение не меняется с течением времени. Направление угловых скоростей показано на рис. 7. Результирующее движение тела будет происходить с угловой скоростью , являющейся векторной суммой двух взаимно перпендикулярных скоростей и

, (8)

поэтому величина угловой скорости равна

.

Мы получили зависимость угловой скорости вращения тела от времени.

По определению угловое ускорение тела равно

,

или с учетом уравнения (8)

.

Вектор – это вектор углового ускорения , направленного вдоль оси в туже сторону, что и вектор , так как по условию задачи тело вдоль этой оси вращается равноускоренно.

Вектор , оставаясь постоянным по модулю, меняет свое направление в пространстве, поворачиваясь вокруг оси с угловым ускорением . Модуль его приращения за промежуток времени (см. рис. 7) равен

,

где – угол поворота вектора вокруг оси за это время. Разделив правую и левую части этого уравнения на , получим

.

Вектор приращения направлен перпендикулярно вектору и лежит в плоскости, перпендикулярной оси , поэтому вектор углового ускорения направлен перпендикулярно вектору . С учетом вышесказанного модуль углового ускорения зависит от времени по закону

.

П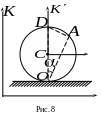 ример 4. Точка находится на ободе колеса радиуса , которое катится без проскальзывания по горизонтальной поверхности со скоростью . Положение точки на ободе задано углом (рис. 8). Найти: а) величину скорости точки ; б) полный путь , проходимый точкой между двумя последовательными моментами ее касания поверхности.

Р е ш е н и е. а) Скорость точки найдем двумя способами.

Для решения задачи первым способом введем две системы отсчета. Неподвижную систему свяжем с горизонтальной поверхностью, а систему – с центром колеса. Система движется поступательно относительно системы со скоростью . В системе колесо вращается вокруг оси, проходящей через точку . Скорости точек, лежащих на ободе колеса, в системе направлены по касательной к окружности и имеют одинаковую величину скорости. Для нахождения величины этой скорости рассмотрим точку . Скорость этой точки в системе отсчета можно найти, воспользовавшись правилом преобразования скоростей,

,

где – скорость точки в системе (см. рис. 9а). Однако, по условию задачи колесо катится без проскальзывания, поэтому . С учетом этого получаем

.

Таким образом, величина скорости всех точек, лежащих на ободе колеса, в системе равна скорости , т.е. .

Для нахождения скорости точки воспользуемся правилом преобразования скоростей

.

Н етрудно доказать, что угол между векторами скоростей и равен (см. рис. 9а и 9б), поэтому

или

.

Для нахождения величины скорости вторым способом, воспользуемся тем, что плоское движение твердого тела можно свести к чисто вращательному движению вокруг мгновенной оси вращения, проходящей через точку (рис. 8), т.к. скорость этой точки в данный момент времени равна нулю. Это означает, что угловые скорости точек и одинаковы или

,

где – длина стороны . Треугольник прямоугольный, поэтому . Таким образом, величина скорости точки равна

.

б) Путь , пройденный точкой между двумя последовательными моментами ее касания поверхности, найдем, воспользовавшись формулой (см. раздел “Кинематика материальной точки”)

. (9)

Точка в системе отсчета (см. рис. 9а) за время переместилась на расстояние , равное

.

С другой стороны, за это время прямая , жестко связанная с колесом, повернулась на угол , поэтому

,

т.е.

,

или

.

Подставляя это выражение в (9) и учитывая, что угол меняется в пре-

делах от до , найдем искомый путь

.

Пример 5. Вращающийся диск (рис. 10) движется в положительном направлении оси . Найти уравнение , характеризующее положение мгновенной оси вращения, если в начальный момент ось диска находилась в точке и в дальнейшем движется с постоянной скоростью , а диск раскручивается без начальной угловой скорости с постоянным угловым ускорением .

Р е ш е н и е. Решим задачу двумя способами.

П е р в ы й с п о с о б. Проведем прямую линию перпендикулярную оси и проходящую через точку (пунктирная линия на рис. 10). Мгновенная ось вращения должна проходить через точку, лежащую на этой прямой. Это обусловлено тем, что прямая, соединяющая мгновенную ось вращения с любой точкой диска, а значит и с точкой , и скорость этой точки взаимно-перпендикулярны. Из этого можно сделать вывод, что координаты точки и мгновенной оси вращения одинаковы. Исходя из этого и учитывая условия задачи, получим зависимость координаты мгновенной оси вращения от времени

. (10)

Для нахождения зависимости координаты мгновенной оси от времени введем вспомогательную систему отсчета , жестко связанную с точкой диска (на рис. 10 эта система не показана). Пусть точка это точка, через которую проходит мгновенная ось вращения. Тогда вектор скорости этой точки относительно системы равен

,

где – скорость точки в системе . По определению скорость равна нулю, поэтому

,

т.е. скорость точки в системе имеет направление противоположное направлению скорости точки в системе . Таким образом, учитывая направление вращения диска, мы приходим к выводу, что координата точки должна быть положительной, как показано на рис. 10. Величина скорости равна

,

где – угловая скорость вращения диска в данный момент времени, равная (см. условие задачи). Отсюда следует, что

. (11)

Исключая время из уравнений (10) и (11), находим уравнение траектории, характеризующее положение мгновенной оси вращения

.

В т о р о й с п о с о б. Напомним, что векторное произведение двух векторов и равно

.

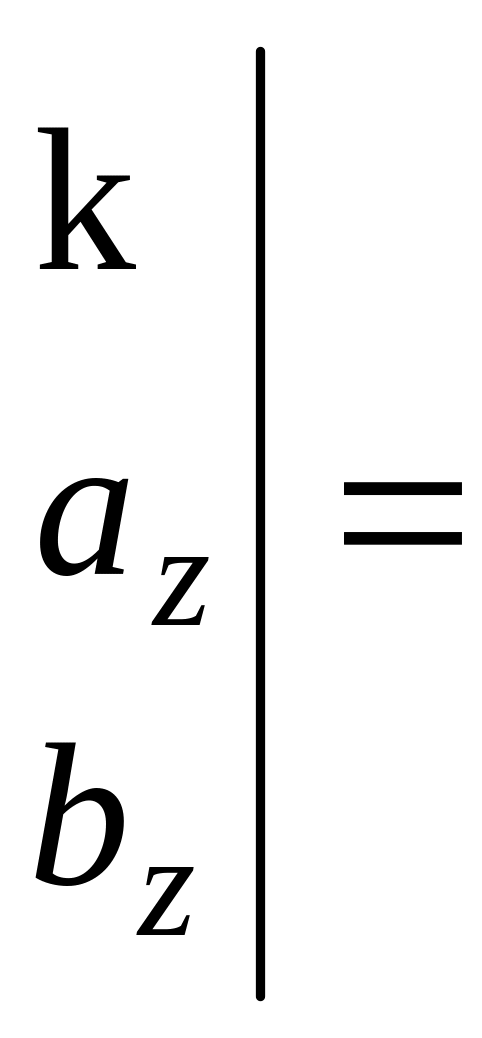
Выберем на диске произвольную точку (рис. 11), положение которой в системе задается вектором равным,

,

где – радиус-вектор этой точки в системе , а – радиус-вектор точки в той же системе отсчета, или в проекциях на координатные оси

, ,

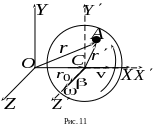Скорость точки в системе , согласно уравнению (4), равна

.

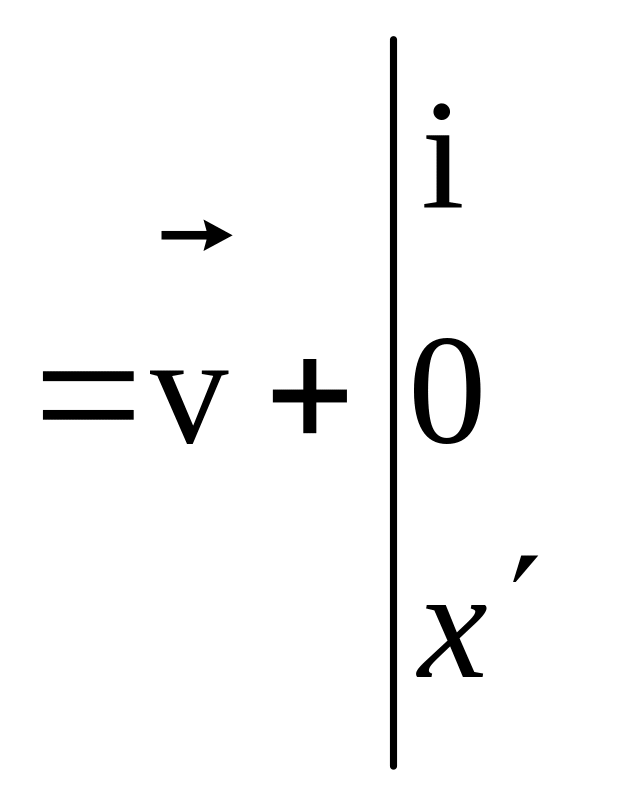
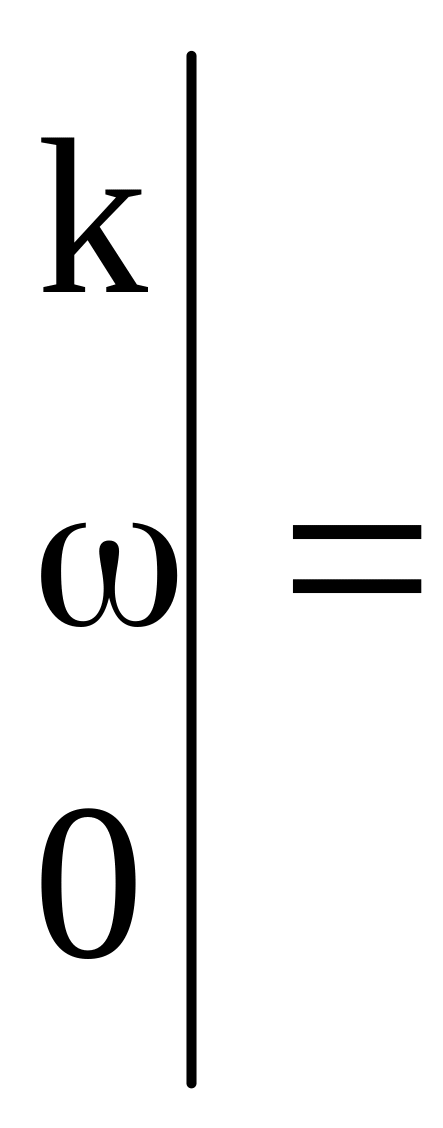
Чтобы точка была расположена на мгновенной оси вращения, должны выполняться условия . Тогда, как следует из последнего уравнения,

.

Исключая из этих выражений время , получим уравнение траектории движения мгновенной оси вращения

.