
10797
.pdf
В качестве |
Г |
рассмотрим график функции |
y = f (x) . Если |
для его наклонной асимптоты |
|
l записать уравнение |
y = kx + d , то коэффициенты k и |
|
d можно найти по формулам
k = lim |
f ( x) |
, |
|
||
x→+∞ |
x |
|
( x→−∞) |
|
|
Выразим теперь
d = lim
x→+∞ ( x→−∞)
y из
f ( x) − kx . |
|
|
|
уравнения (2.2):
y = ± b 
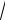 x2 − a2 и используем для полученных двух a
x2 − a2 и используем для полученных двух a
функций эти формулы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
b |
|
|
|
|
a |
|
2 |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|||||||
|
|
|
lim |
|
|
|
|
|
= lim ± |
|
|
|
1 − |
|
|
|
= ± |
|
|
|
; |
|
|
|||||||||||||||||||||
|
|
|
|
|
x |
|
|
a |
|
|
|
|
a |
|
|
|||||||||||||||||||||||||||||
|
|
x→+∞ |
|
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
( x→−∞) |
|
|
|
|
|
( x→−∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
lim f |
|
( x) − kx = |
|
|
|
|
|
± |
b |
|
|
|
|
|
|
|
|
|
M |
b |
x |
= |
|
||||||||||||||||||||
|
lim |
|
|
|
|
x2 − a2 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
( x→−∞) |
|
|
|
|
|
|
|
|
|
|
( x→−∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
− x)( |
|
|
|
|
|
|
+ x) |
|
|
|
|
||||||||||||||||||
|
|
= ± |
b |
|
|
|
|
|
x2 − a2 |
|
|
x2 − a2 |
= |
|
||||||||||||||||||||||||||||||
|
|
|
|
lim |
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
+ x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
a |
|
|
x→+∞ |
|
|
|
|
|
|
x |
2 |
− a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
( x→−∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= ± |
b |
lim |
|
x2 − a2 − x2 |
= ± |
b |
|
lim |
|
|
|
|
|
|
−a2 |
|
|
|
|
|
|
= 0. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
a |
x→+∞ |
|
|
x |
2 |
− a |
2 |
+ x |
|
|
|
a |
x→+∞ |
|
|
|
x |
2 |
− a |
2 |
+ x |
|
|
||||||||||||||||||||
|
( x→−∞) |
|
|
|
|
|
|
|
|
( x→−∞) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Следовательно, |
прямые |
|
|
y = ± |
b |
x |
|
|
являются |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
x → +∞ и |
|||||||
наклонными |
|
асимптотами |
|
гиперболы |
|
|
при |
|
|
|||||||||||||||||||||||||||||||||||
при |
x → −∞ . |
Поэтому |
построение |
|
|
гиперболы |
по |
|||||||||||||||||||||||||||||||||||||
каноническому |
уравнению |
|
|
|
(2.2) |
|
следует |
|
|
|
начинать |
с |
||||||||||||||||||||||||||||||||
30
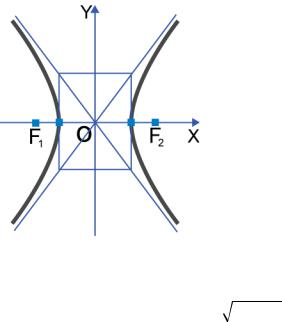
изображения основного прямоугольника, продолжая диагонали которого получаем прямые с уравнениями
y = ± |
b |
x . |
Обе |
бесконечные |
ветви |
рисуем |
|
||||||
|
a |
|
|
|
|
|
неограниченно приближающимися к ним (рис. 2.11).
Рис. 2.11
Фокусы находятся на расстоянии c = 
 a2 + b2 от начала координат.
a2 + b2 от начала координат.
Гипербола с равными полуосями называется равносторонней, её каноническое уравнение имеет вид x2 − y2 = a2 . Основной прямоугольник равносторонней гиперболы становится квадратом, прямые y = x и y = −x являются асимптотами, перпендикулярными друг к другу (рис. 2.12).
31
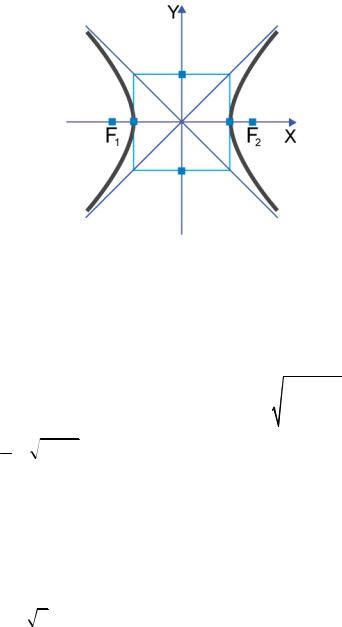
Рис. 2.12
Отношение расстояния между фокусами к расстоянию между вершинами гиперболы называется эксцентриситетом гиперболы и обозначается буквой ε :
ε = |
c |
. |
Для гиперболы ε > 1, поскольку |
c > a . Так как |
|||||||||||||
|
|||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
+ b2 |
b 2 |
|
|
|||||||
ε |
2 |
|
|
c2 |
|
a2 |
b 2 |
|
|||||||||
|
= |
|
|
|
= |
|
|
|
= 1 + |
|
, то ε = |
1 + |
|
|
и |
||
|
a |
2 |
|
a |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
a |
a |
|
|||||||
b = 
 ε 2 −1 . a
ε 2 −1 . a
Следовательно, как и для эллипса, эксцентриситет гиперболы определяется отношением её осей. Он характеризует форму её основного прямоугольника. Чем меньше эксцентриситет, тем меньше отношение b к a , то есть основной прямоугольник более вытянут в направлении действительной оси. Для равносторонней гиперболы
ε = 
 2 .
2 .
32

2.4. Ещё одна знаменитая кривая второго порядка – это парабола. Для её определения нужна прямая L на плоскости и не лежащая на прямой точка F . Множество всех точек плоскости, равноудалённых от данной точки F (называемой фокусом) и данной прямой L (называемой директрисой), называется параболой. Расстояние от фокуса до директрисы параболы принято обозначать через p (рис. 2.13).
Величину p называют фокальным параметром параболы.
Рис. 2.13
Для получения уравнения параболы необходимо ввести систему координат на плоскости. Проведём ось абсцисс через фокус параболы перпендикулярно директрисе и будем считать её направленной от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис. 2.14).
33
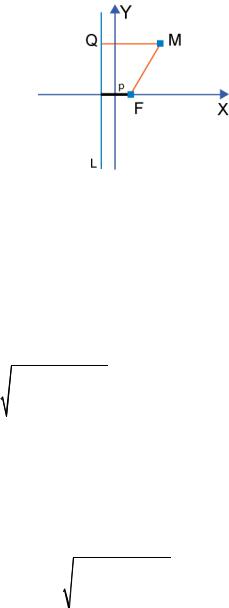
Рис. 2.14
Тогда фокус F приобретёт координаты
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;0 , |
а |
уравнение директрисы в |
этой |
системе |
|||||||||||||||||||
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координат будет иметь вид |
x = − |
p |
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
M параболы |
||||
|
|
|
Координаты произвольной точки |
||||||||||||||||||||||
обозначим |
x , |
|
y |
и |
|
запишем |
|
расстояние |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
MF = |
x − |
|
|
+ y |
|
|
. |
|
Расстояние |
|
|
от |
|
M |
до |
||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
директрисы равно MQ , где Q - |
|
основание |
|||||||||||||||||||||||
перпендикуляра, |
опущенного |
|
из M |
|
|
на |
директрису. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
p |
|
|
Поскольку |
Q |
имеет |
координаты |
|
|
; y , |
то |
||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
MQ = x + |
p |
. Тогда для параболы получаем |
|
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
|
2 |
|
|
|
|
p |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x − |
|
|
|
+ y |
|
= x + |
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|

Возведём обе части полученного равенства в квадрат
x2 − px + |
p2 |
+ y2 = x2 + px + |
p2 |
|
|
|
|
|
|
||||
4 |
4 |
|
|
|||
и запишем каноническое уравнение параболы |
|
|||||
|
|
|
|
|
||
|
|
y2 = 2 px . |
(2.3) |
|||
|
|
|
|
|
|
|
Как уравнения эллипса и гиперболы, оно тоже является уравнением второго порядка.
Так как уравнение (2.3) содержит переменную y только в чётной степени, то парабола симметрична
относительно оси Ox . Так как p > 0 , то x ³ 0 . Это означает, что парабола расположена справа от оси Oy .
При x = 0 получаем y = 0 . |
|
|
|
При возрастании |
x возрастает и y , причём, |
||
если x → +∞ , то y → +∞ . |
Построив в первой четверти |
||
график функции y = |
|
|
, и, отразив его |
|
2 px |
||
симметрично относительно оси Ox , получим геометрическое изображение параболы (рис. 2.15).
Рис. 2.15
35
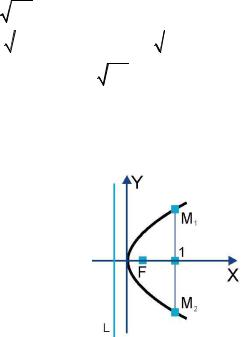
Ось симметрии параболы (в данном случае совпадающая с осью Ox ) называется её осью. Точка, в которой парабола пересекает свою ось, называется её вершиной (в нашем случае вершина совпадает с началом координат). Для описания геометрического смысла фокального параметра p можно взять какое-
либо значение абсциссы, например, x = 1 . Из уравнения (2.3) найдём соответствующие ему значения ординаты:
y = ± |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p . |
Это |
даёт |
на |
|
параболе две |
точки |
|||||||
M1 (1; |
|
) |
|
M 2 (1; − |
|
) , расстояние |
|
||||||
2 p |
и |
2 p |
между |
||||||||||
|
|
|
|
|
|
|
|||||||
которыми равно |
2 |
|
2 p |
(рис. |
2.16). Тем самым, чем |
||||||||
больше |
|
|
p , |
|
тем |
|
больше |
|
расстояние |
M1M 2 . |
|||
Следовательно, параметр p характеризует «ширину» области, ограниченной параболой.
Рис. 2.16
В трёх рассмотренных случаях мы двигались от определений конкретных линий к их уравнениям, которые оказались уравнениями второго порядка. Можно поставить обратную задачу: начать сразу с анализа уравнения.
36

2.5. Рассмотрим уравнение вида |
|
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 , |
(2.4) |
где коэффициенты A, B,C, D, E и F — |
любые |
действительные числа, но, по крайней мере, одно из
чисел A , B |
или C |
отлично от |
нуля |
(т.е. |
A2 + B2 + C 2 ¹ 0 ). |
Оно |
называется |
общим |
|
уравнением линии (кривой) второго порядка. |
|
|||
Например, уравнение x2 + xy + y2 - y - |
5 = 0 |
|||
относится к классу уравнений второго порядка и получается из общего вида (2.4) при конкретном
значении коэффициентов: A = 1 , B = 0,5 , |
C = 1, |
D = 0 , E = - 0,5 , F = - 5 . |
|
Кроме рассмотренных классических |
кривых |
(эллипса, гиперболы и параболы), уравнение (2.4) может привести ещё к нескольким случаям, называемым вырожденными.
Если в уравнении (2.4) B = D = E = F = 0 , то
остаётся только два слагаемых, т.е. |
Ax2 + Cy2 = 0 . |
|||||||||||
При одинаковых знаках A и C уравнению |
||||||||||||
соответствует |
на |
плоскости |
одна |
точка |
– |
начало |
||||||
координат. При разных |
знаках |
A |
и |
C |
– |
пара |
||||||
|
|
|
|
|
|
|
|
|
||||
пересекающихся прямых |
y = ± − |
A |
|
x . |
|
|
|
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
C |
|
|
|
|
||
Если в уравнении (2.4) остаются ненулевыми |
||||||||||||
два других слагаемых, например, |
оно |
имеет |
вид |
|||||||||
Cy2 + F = 0 , |
то |
возможны |
|
две |
ситуации: |
при |
||||||
одинаковых знаках коэффициентов C и F решений нет, а при разных знаках C и F получаются две параллельные прямые.
37
Если из уравнения (2.4) остаётся одно слагаемое
Cy2 = 0 или |
Ax2 = 0 , то на плоскости |
получается |
||
одна прямая. |
Если |
B = D = E = 0 |
и в |
уравнении |
Ax2 + Cy2 + F = 0 |
коэффициенты |
A > 0 , C > 0, |
||
F > 0, то опять ему не удовлетворяют координаты ни одной точки плоскости.
2.6. Итак, после преобразований уравнения (2.4) получаются три основные линии: эллипс, гипербола и парабола или линии, отнесённые к вырожденным случаям. Все эти ситуации разбиваются на три типа, соответствующие трём основным линиям.
I. Эллиптический тип:
1) |
x2 |
+ |
y2 |
|
= 1 (эллипс или окружность), |
|
a2 |
b2 |
|
||||
|
|
|
|
|
||
2) |
x2 |
+ |
y2 |
|
= 0 (точка), |
|
a2 |
b2 |
|
||||
|
|
|
|
|
||
3) |
x2 |
|
+ |
y2 |
|
= - 1 (пустое множество). |
a2 |
|
b2 |
|
|||
|
|
|
|
|
||
II. Гиперболический тип:
4) |
x2 |
- |
y2 |
= 1 (гипербола), |
|
a2 |
b2 |
||||
|
|
|
38
5) |
x2 |
- |
y2 |
= 0 (пара пересекающихся |
|
a2 |
b2 |
||||
|
|
|
прямых).
III. Параболический тип:
6)y2 = 2 px (парабола),
7)y2 = a2 (пара параллельных прямых),
8)y2 = 0 (прямая),
9)y2 = - a2 (пустое множество).
Если для каждого из уравнений вычислить число
AC − B2 , то можно заметить, что оно положительно для уравнений первого типа, отрицательно для второго и равно нулю для уравнений третьего типа. Оказывается, это выполняется в общем случае. То есть по исходным коэффициентам уравнения (2.4), которые присутствуют в конкретной задаче, можно сразу определить, к какому типу относится линия, задаваемая этим уравнением:
I. |
Если |
AC − B2 > 0 , то уравнение задаёт линию, |
|
относящуюся к эллиптическому типу (случаи 1; 2 |
|
|
или 3). |
AC − B2 < 0 , то уравнение задаёт линию, |
II. |
Если |
|
|
относящуюся к гиперболическому типу (случаи 4 |
|
|
или 5). |
|
39
