10797

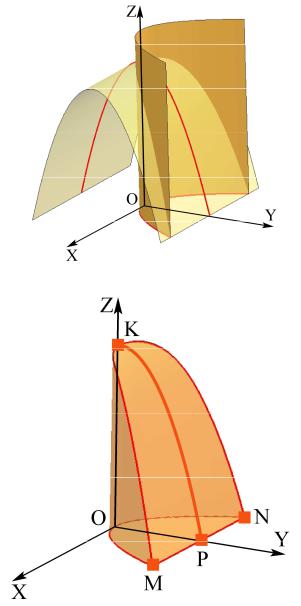
Рис. 3.44

Рис. 3.45

100

ГЛАВА 4

ОБРИСОВКА КОНТУРОВ или

ПОДБОР КРИВЫХ И ПОВЕРХНОСТЕЙ

Чтобы воспользоваться рассмотренным в предыдущих главах материалом для решения поставленной задачи, нужно соотнести дизайнерский образ с геометрическими формами классических поверхностей. Будем исходить из принципов гармоничного формообразования объекта, с которым мы работаем. Сначала сделаем предварительный эскиз двух сечений по плоскостям симметрии бутылки (рис.

4.1).

Рис. 4.1

101

Далее разделим сложный объём, ограниченный поверхностью бутылки на пять частей, чтобы каждую часть представить ограниченной своим видом поверхности второго порядка (рис. 4.2). Тем самым мы формируем геометрическую модель бутылки, не детализируя вопросы стыковки отдельных частей. Предполагаем, что при изготовлении будет использоваться компьютерный вариант модели, в котором эти вопросы будут увязаны.

Рис. 4.2

Представим границу сечения верхней части V1 в виде равносторонней гиперболы

(рис. 4.3). Начало системы координат xOz совместим с центром гиперболы.

102

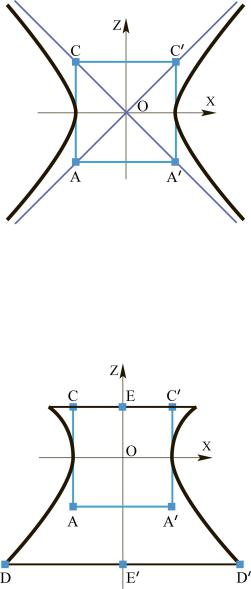
Рис. 4.3

Построив гиперболу, срежем её по горизонтали: сверху – продолжив верхнюю сторону CC′ квадрата, снизу – по линии DD′ на расстоянии EE′ = 3, 6 см от стороны CC′ (рис. 4.4).

Рис. 4.4

103

Рассмотрим в пространстве систему координат (x, y, z) , добавив ось Oy к исходной системе xOz . Верхнюю часть V1 теперь можно представить в виде

пространственной области, ограниченной однополостным гиперболоидом и плоскостями z = c и z = d , параллельными координатной плоскости xOy

(рис. 4.5). Объём υ(V1 ) будем вычислять по формуле, полученной в первой главе:

d

υ(V1 ) = ∫ Q(z)dz . c

Рис. 4.5

Следующий шаг – получение зависимости площади сечений гиперболоида плоскостями,

параллельными xOy , от координаты z . В связи с тем,

что сечение горлышка должно быть круглым, а сечение основной части бутылки предполагалось сделать в виде эллипса, область V1 нужно разделить на две части.

104

Верхняя часть V1 - горлышко V11 - будет ограничена гиперболоидом вращения с равными

полуосями a = b = c = 1 AA′ = 1,1 и уравнением

2

x2 + y2 − z2 = 1. 1, 21 1, 21 1, 21

Уравнение окружности, являющейся сечением гиперболоида плоскостью, параллельной координатной

плоскости xOy , получается, если зафиксировать значение z :

Радиус rz этой окружности имеет разные значения в зависимости от координаты z : rz = 1, 21+ z2 , а

площадь Q(z) = π rz 2 = π (1, 21+ z2 ) .

Высоту отсечённого элемента V11 задаём, исходя из размера эскиза: EO′ = 1,9 . Это даёт пределы изменения координаты z : −0,8 ≤ z ≤ 1,1. Поэтому

1,1

υ(V11 ) = ∫ π (1, 21+ z2 )dz .

−0,8

Чтобы довести решение до числового ответа, необходимо уметь вычислять определённый интеграл хотя бы в самых простых ситуациях. Это требует знакомства с основами математического анализа.

105

Итак, в нашем случае

= π (1, 21×1,1+ 1,13 ) -π (-1, 21×0,8 - 0,83 ) = 9,147 .

Переход от горлышка к широкой части бутылки обозначим V12 , и будем рассматривать его в виде

области, ограниченной плоскостями, параллельными плоскости xO y и однополостным гиперболоидом,

сплюснутым по оси Oy . Систему координат оставляем прежней. В ней уравнение гиперболоида примет вид

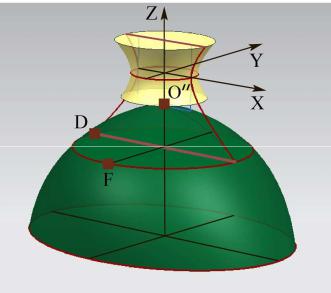
Чтобы найти величину полуоси b , учтём присутствие на поверхности бутылки точки F , которая находится на эскизе в плоскости yOz на расстоянии EE′ = 3, 6 см от плоскости верхнего края (рис. 4.5).

Измерение даёт координаты в системе (x, y, z) : F (0; −2, 2; −2,5) . Для удовлетворения этого условия

необходимо значение b , которое получается из уравнения гиперболоида при подстановке в него x = 0 ; y = −2, 2 ; z = −2,5 :

1, 21 0,785 1, 21

Зафиксировав значение z в (4.2), придём к уравнению эллипса, являющегося сечением гиперболоида плоскостью, параллельной координатной плоскости xOy :

При каждом конкретном значении z получается эллипс со своими полуосями az и bz :

Значение площади Q(z) в этом случае

Q(z) = π a b = π 0,785 (1, 21+ z2 ) .

Поэтому

107

Суммируя полученные значения, найдём объём верхней части бутылки:

υ(V1 )=υ(V11 )+υ(V12 )=27,07 см3 .

Рис. 4.6

108

Для нахождения параметров p и q в уравнении

(4.3) учтём присутствие на параболоиде точек D и F , расположенных на гиперболоиде. Координаты точки

F известны, а для нахождения координаты xd точки D подставляем в уравнение (4.2) y = 0 и z = −2,5 :

Чтобы подобрать форму параболоида, без излома соединяющегося с гиперболоидом, состыкуем эти

поверхности в сечении плоскостью Для выполнения такого условия в точке D стыкующиеся гипербола и парабола должны иметь одинаковый наклон касательной. Это обеспечивается равенством производной в этой точке.

Вернувшись к уравнению (4.1) гиперболы в плоскости xOz , выразим z = ±x2 −1, 21 и найдём производную соответствующих функций:

109