
9957
.pdf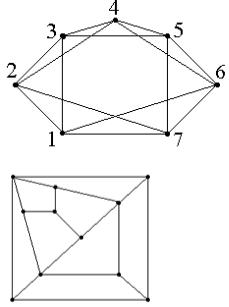
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 1 |
0 |
0 |
0 |
1 |
1 |
1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 0 1 0 0 |
0 |
1 |
1 |
|
1 0 |
1 |
1 |
1 |
1 |
1 |
0 |
|||||||||||
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
|
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1) |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
2) |
0 0 1 0 1 |
0 |
0 |
0 |
3) |
0 1 |
1 |
0 |
1 |
0 |
0 |
0 |
|||||||||||
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
1 |
0 1 |
1 |
0 |
1 |
1 |
1 |
|
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
|
0 0 0 0 1 |
0 |
0 |
1 |
|
|
1 1 |
1 |
1 |
1 |
0 |
1 |
0 |
|
||||||||
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|||
|
|
|
1 |
0 |
0 |
0 |
0 |
1 |
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
|
|
|
1 |
0 |
|
1 |
0 |
|
1 |
0 |
||||||||||||||||||||||||
9. Транспортная компания осуществляет грузовые перевозки в города A, B, C, D, E, F, G. В таблице приведена матрица смежности графа рейсов компании.
|
A |
B |
C |
D |
E |
F |
G |
|
|
|
|
|
|
|
|
A |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
B |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
C |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
D |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
E |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
F |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
G |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
Нужно задать граф диаграммой и матрицей инцидентности. Установите последовательность городов (гамильтонов цикл) с началом в городе D,
проходящую через все города ровно один раз с возвращением в D, при условии,
что город F был посещен после города А. 10.Существуют ли в полном двудольном
графе K3,3 и в графе G, заданном на рисунке 3.80,
эйлеров цикл, гамильтонов цикл, эйлерова цепь,
гамильтонова цепь? Укажите их или докажите их
отсутствие.
Рис. 3.80.
11.Является ли данный граф на рисунке 3.81
гамильтоновым?
Рис. 3.81.

171
12. На рисунке 3.82. изображен план подземелья, в одной из комнат которого скрыты богатства рыцаря. После смерти рыцаря его наследники нашили завещание, в котором было сказано, что для отыскания сокровищ достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причем в точности по одному разу через каждую. Сокровища скрыты за той дверью, которая будет пройдена последней. В какой комнате были скрыты сокровища?
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
6 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
9 |
|
|
10 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
||
16 |
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|||
|
20 |
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.82.
13.Сможет ли экскурсовод провести посетителей по выставке так, чтобы они побывали в каждом зале ровно один раз (рис.3.83.)? Вершины графа – это вход,
выход, двери, соединяющие залы, перекрестки, а ребра – залы и коридоры. Где на выставке следовало бы сделать вход и выход, чтобы можно было провести экскурсию по всем залам, побывав в каждом из них в точности один раз?
Рис.3.83.

172
14.В небольшой роще находится заяц (рис.3.84). Выскочив из норы и бегая по снегу от дерева к дереву, он оставил следы и, наконец, спрятался под одним из этих деревьев. Где находится сейчас заяц? Под каким деревом находится его нора? Сколько решений имеет задача?
рис.3.84.
3.5.Деревья.
Понятие дерева как математического объекта было впервые предложено Кирхгофом в связи с определением фундаментальных циклов, применяемых при анализе электрических цепей. Деревья имеют особое положение в теории графов из-за предельной простоты строения, и часто при решении какой-либо задачи на графах ее сначала анализируют на деревьях.
Определение 11. Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется лесом. Таким образом, деревья являются компонентами леса.
Рис. 3.85. Граф – дерево |
Рис.3.86. Лес (из трех деревьев) |
173
В произвольном графе G вершина а называется концевой (листом), если deg(a)=1. Инцидентное ей ребро называется концевым ребром.
Корнем (центром) в дереве называется вершина с минимальным эксцентриситетом. Эксцентриситет вершины v – это длина кратчайшего пути от вершины v до самой удаленной от нее вершины. Центр дерева состоит из одной вершины или двух смежных вершин.
Нулевое дерево – это дерево, не имеющее ни одной вершины.
Построение дерева начинается с корня дерева, который является единственной вершиной «первого уровня». Далее идут вершины «второго уровня» и т.д., где вершины очередного уровня (каждая из вершин) будут связаны ровно с одной вершиной предыдущего уровня и не будут иметь никаких иных связей. Верхняя вершина называется предком для связных с ней нижних вершин, а нижние вершины – потомками соответствующей верхней вершины. На любом дереве существует единственная вершина, не имеющая предка – корень, и может быть сколько угодно вершин, не имеющих потомков
– листьев. Все остальные вершины имеют ровно одного предка и сколь угодно потомков.
Примерами деревьев могут служить генеалогические и организационные диаграммы. Деревья используются для организации информации в системах управления базами данных (иерархическая база данных может быть представлена деревом с корнем) и для представления синтаксических структур в компиляторах программ.
Пусть G =(V,E) и V =n, E =m. Тогда справедливы следующие
утверждения:
1.G – дерево. G – связный граф и m=n-1.
2.G – ациклический граф, обладающий тем свойством, что если какую-
либо пару его несмежных вершин соединить ребром, то полученный граф
будет содержать ровно один цикл.
3. G – ациклический граф и m=n-1.
174
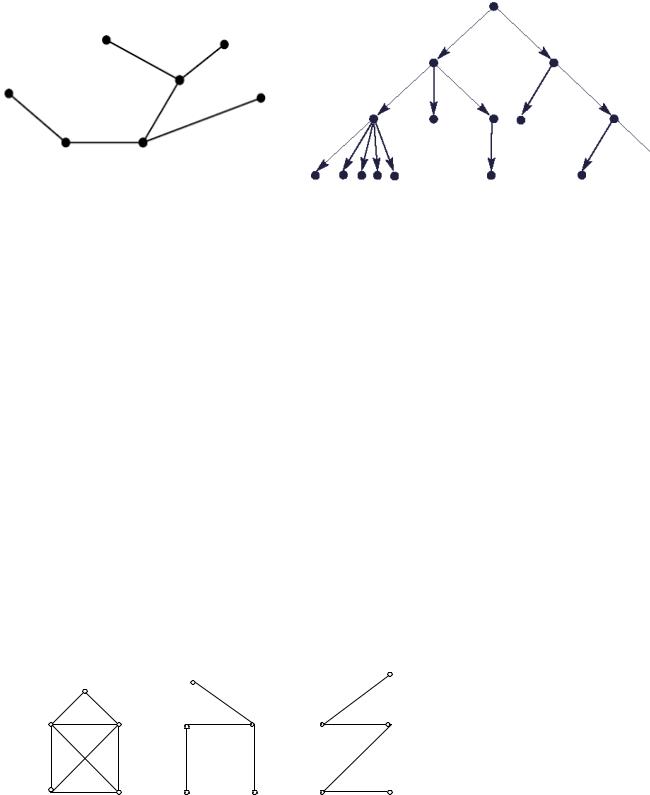
4.Любые две несовпадающие вершины графа соединяет единственная простая цепь.
Рис.3.87. Граф – неориентированное
дерево.
Рис.3.88. Ориентированное дерево
Определение 12. Ориентированный граф называется ориентированным
деревом, если: 1) существует ровно одна вершина х0 V , называемая корнем,
которая не имеет предшествующих вершин; 2) любой вершине x j ¹ х1 в графе
Gнепосредственно предшествует ровно одна вершина.
Вориентированном дереве полустепень захода каждой вершины (за исключением корня) равна 1, а полустепень корня дерева равна 0.
Двоичным деревом называется ориентированное дерево, полустепень
исхода каждой вершины которого не превышает 2.
Для графов, которые сами по себе не являются деревьями, вводится
понятие остовного дерева.
Подграф G′ = (V ′, E ) графа G = (V , E ) называется остовным поддеревом
(остовным каркасом), если V ′ = V и G – дерево, т.е. остовной подграф получается из исходного графа удалением только ребер без удаления вершин.
(1) |
(2) |
(3) |
Рис.3.89. Граф G (1) и два его остова (2) и (3).
175
Часто, особенно когда графы используются для моделирования реальных
систем, их вершинам или ребрам приписываются некоторые числа (веса). Граф,
сзаданными весами вершин и/или ребер называется взвешенным
(нагруженным) графом. Глубина вершины определяется как длина пути от нее к корню дерева. Глубина графа – это максимальная глубина его вершин.
Кратчайший остов взвешенного графа G – это остов, у которого сумма весов ребер наименьшая. Кратчайшее остовное дерево находит применение при решении задач, в которых необходимо связать n точек некоторой сетью так,
чтобы общая длина «линий связей» была минимальной (прокладка дорог,
газопроводов, линий электропередач).
Порожденный подграф графа G = (V , E ) – |
это такой граф G |
′ |
|
′ ′ |
), у |
|||||||
|
= (V , E |
|||||||||||
которого V |
′ |
V , |
Е |
′ |
= {(а, б) Е |
|
′ |
т.е. порожденный |
подграф |
|||
|
||||||||||||
|
|
|
а, б V }, |
|||||||||
получается из исходного графа удалением вершин и всех ребер, инцидентных удаленным вершинам.
Свойство 1. Любое конечное дерево имеет хотя бы две концевые вершины и одно концевое ребро.
Свойство 2. Дерево с n вершинами содержит n-1 ребро.
Доказательство. Простейшее дерево имеет только одно ребро и две вершины. Каждый раз, добавляя еще одно ребро в конце ветви, прибавляем также и вершину.
Свойство 3. Лес, состоящий из k компонент и имеющий n вершин,
содержит n- k ребер.
Доказательство следует из того факта, что для каждой компоненты выполнено свойство 2, а именно число ребер на 1 меньше числа вершин,
следовательно, для k компонент число ребер будет меньше числа вершин на k.
Таким образом, если в графе n вершин, то число ребер будет n- k.■
Свойство 4 (Теорема Кэли). Число различных деревьев, которые можно построить на n различных вершинах, равно nn−2 .
|
|
|
|
176 |
Доказательство. Пусть G − |
дерево с n вершинами V = {a1, a2 ,…, an }. |
|||
Пусть а1 |
− |
лист в дереве G , а b1 |
− смежная с ним вершина. Удалив из G |
|
вершину |
а1 |
и ребро |
e1 = (а1,b1 ) , |
получим дерево G1 , к которому также |
применим |
описанную |
процедуру. |
Повторяем ее до тех пор, пока после |
|
удаления вершины аn − 2 и ребра en − 2 = (аn − 2 ,bn − 2 ) не получим дерево Gn − 2 ,
состоящее из одного ребра en −1 = (аn −1,bn −1 ) . Дереву G поставим в соответствие упорядоченный набор вершин p(G) = (b1,…,bn − 2 ) , где каждая вершина bi может быть любой из множества V. По теореме умножения из комбинаторики всего различных наборов p(G) можно составить nn−2
способами, а значит число различных деревьев, которые можно построить на n
различных вершинах, равно nn−2 ■.
Свойство 5. Последовательность целых чисел d1 , d2 ,…, dn является
последовательностью степеней вершин некоторого дерева на n вершинах тогда
n
и только тогда, когда : 1) каждое di ³1, i = 1,2,…, n и 2) ∑ deg(vi ) = 2n - 2 .
i =1
Пример. 3.30. Даны последовательности чисел: а) 1, 1, 2, 3, 5, 5, 6; б) 4, 5, 6, 7; в) 1, 1, 1, 3; г) 1, 1, 1, 1, 1, 2, 3, 4. Проверим, можно ли построить дерево,
такое, что данная последовательность чисел являлась бы последовательностью степеней вершин этого дерева.
n
Ответ: а) нет, т. к. ∑ deg(vi ) =17 ¹ 2n - 2 ; б) нет, так как нет ни одной висячей
i =1
вершины ( deg(v) ¹ 1) ; в) да, так как выполняются условия свойства 5; г) да, так как выполняются условия теоремы.
Теорема 6. Число ребер произвольного неориентированного графа G ,
которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m - n + k , где m – число ребер графа, n – число вершин графа, k – число компонент связности графа.
177
Доказательство. Рассмотрим i-тую компоненту связности Gi графа G .
Пусть Gi содержит ni вершин. Тогда остов Gi′ графа Gi , являясь деревом,
содержит ni −1 ребро. Следовательно, для получения Gi′ из компоненты Gi
нужно удалить |
mi − (ni − 1) ребер, где mi |
– число ребер в Gi . |
|||
Просуммируем |
удаляемые |
ребра |
по |
всем компонентам связности, |
|
k |
= m , |
k |
k |
|
− 1) = m − n + k .■ |
получим ∑ mi |
∑ ni = n , |
∑ mi − (ni |
|||
i =1 |
|
i =1 |
i =1 |
|
|
Определение 12. Число ν (G) = m − n + k называется цикломатическим
числом графа G , число ν * (G) = n − k коциклическим рангом или корангом.
Оно равно числу ребер, входящему в любой остов графа G .
Очевидно, что ν (G) +ν * (G) = m .
Следствие 1. Неориентированный граф G является деревом тогда и только тогда, когда ν (G) = 0.
Следствие 2. Неориентированный граф G имеет единственный цикл тогда и только тогда, когда ν (G) = 1.
Физический смысл цикломатического числа: оно равно наибольшему числу независимых циклов в графе. При расчете электрических цепей цикломатическим числом можно пользоваться для определения независимых
контуров.
Примеры 3.30.
1) Для полного графа К5 (5 вершин, С52 = 10 ребер) цикломатическое число
равно ν (К5 ) = 10 − 5 + 1 = 6 .
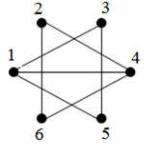
2) Для графа на рисунке 3.90
ν (G) = 7 − 6 + 1 = 2 .
Рис. 3.90.

178
Кодирование деревьев
Каждому корневому дереву с m ребрами можно взаимно однозначно сопоставить двоичный вектор длины 2m, называемый кодом дерева.
Построение кодового дерева начинается с корня дерева, каждая вершина может породить не более двух вершин, причем левой вершине будет соответствовать 0, а правой 1. Концевые вершины соответствуют кодовым словам. Пример кодового дерева на рисунке 3.91.
Рис. 3.91. Кодовое дерево
Утверждение. Для того, чтобы последовательность нулей и единиц являлась кодом некоторого дерева, необходимо и достаточно, чтобы число нулей и единиц в последовательности было одинаковым, причем в любом начальном отрезке последовательности количество нулей было не меньше количества единиц.
Например, последовательность (0011101001) не может быть бинарным кодом дерева, поскольку в отрезке 00111 из пяти первых цифр этой последовательности единиц больше, чем нулей.
Чтобы построить корневое дерево по коду из нулей и единиц, нужно разбить последовательность на пары 0 и 1, следуя правилу: первая попавшая в коде единица образует пару с предшествующим нулем; каждая следующая единица образует пару с ближайшим слева неиспользованным нулем. Если образованные таким образом пары пометить снизу кода фигурными скобками,
то каждая такая скобка будет соответствовать ребру графа.
179
Пример 3.31. Построить дерево по коду (010010010111010011).
Разобьем элементы последовательности на пары и построим дерево на рисунке 3.92:
01001001011010011
1 |
2 |
|
7 |
|
|
3 |
4 |
8 |
|||
|
|
|
5 |
|
9 |
|
|
|
|
||
|
|
6 |
|
|
|
Рис.3.92.
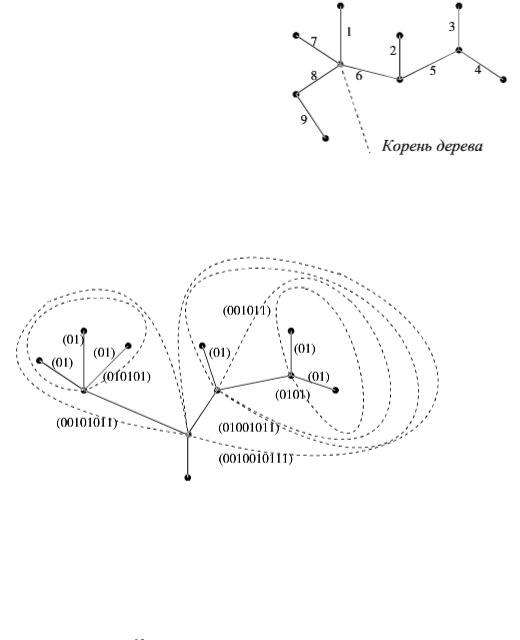
Пример 3.32. Построить бинарный код дерева, изображенного на
рисунке 3.93.
Рис.3.93. Бинарное кодовое дерево.
Этапы построения бинарного кода указаны на рисунке 3.93.
Ответ: 001010110010010111.
Семантическое дерево – это двоичное дерево, корень которого помечен булевой функцией от  переменных, из каждого узла идут по два ребра: одно соответствует нулевому значению соответствующей переменной (его изображают штриховой линией), а другое – единичному значению этой переменной (оно изображается сплошной линией). Таким образом, каждой ветви от корня до листа сопоставляется набор значений переменных, а листья помечаются соответствующими значениями функции.
переменных, из каждого узла идут по два ребра: одно соответствует нулевому значению соответствующей переменной (его изображают штриховой линией), а другое – единичному значению этой переменной (оно изображается сплошной линией). Таким образом, каждой ветви от корня до листа сопоставляется набор значений переменных, а листья помечаются соответствующими значениями функции.
Семантическое дерево соответствует вычислению булевой функции
