9957

140

(xn , x1 ). Но тогда x1, x2 ,…, xn , x1 – простой цикл в исходном графе,

проходящий через ребро (a,b).■

Свойство 3. Если в графе степень каждой вершины не меньше 2, то в

нем есть цикл.

Доказательство. Найдем в графе простой путь наибольшей длины (он существует, так как длина простого пути не может превышать n −1). Пусть это x1, x2 ,…, xn . Вершина xn смежна с xn −1 , а так как ее степень не меньше двух,

то она смежна еще хотя бы с одной вершиной, скажем, с y. Если вершина y

была бы отлична от всех вершин пути, то последовательность x1, x2 ,…, xn , y

Свойство 4. Если у графа все простые циклы четной длины, то граф не

имеет ни одного цикла нечетной длины.

Доказательство. Для графа, являющегося простым циклом, утверждение очевидно. Допустим, что у графа, все простые циклы которого четной длины,

все же найдется цикл нечетной длины. Во всяком непростом цикле существует вершина, через которую путь проходит более одного раза. В такой вершине цикл разобьется на два, причем один из них, очевидно, будет иметь нечетную длину, а другой – четную. Будем продолжать расчленение нечетного цикла до тех пор, пока не дойдем до простых циклов. Хотя бы один из них должен иметь нечетную длину. Существование такого простого цикла противоречило бы условию. Следовательно, принятое предположение неверно. Значит, верно, что если у графа все простые циклы четной длины, то граф не имеет ни одного цикла нечетной длины. ■

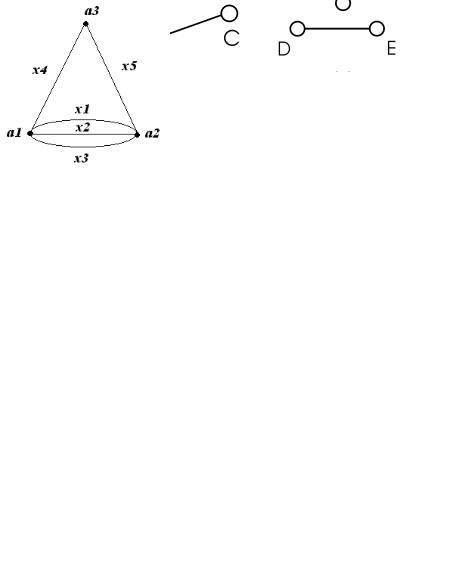
Проиллюстрируем введенные понятия для графа на рис. 3.47.

a2 x2a1x1a2 , a1x1a2 x5a3 x4a1 и a2 x5a3 x4a1x3a2 .

Две вершины графа A и B называются связанными, если в графе существует маршрут с концами A и B. Связанные маршрутом вершины связаны также и простой цепью. Отношение связанности вершин обладает свойствам эквивалентности и определяет разбиение множества вершин графа на непересекающиеся подмножества.

Граф называется связным, если в нем для любых двух вершин имеется маршрут, соединяющий эти вершины. Заметим, что по свойству 1 можно в этом определении заменить слово «маршрут» словами «простая цепь».

Все подграфы графа связны и называются связными компонентами

графа. Для каждого н-графа верно G = G(Hi ) .

i

142

Для произвольного графа определим на множестве вершин отношение соединимости: вершина a соединима с вершиной b, если существует соединяющий их маршрут. Легко видеть, что это отношение рефлексивно,

симметрично и транзитивно, то есть является отношением эквивалентности.

Классы эквивалентности называются областями связности, а порождаемые ими подграфы – компонентами связности графа. В связном графе имеется только одна компонента связности – весь граф. Компоненты связности можно определить также как связные подграфы данного графа. У графа на рис.3.44 в)

две компоненты связности.

Ребро, при удалении которого увеличивается число компонент связности,

называется перешейком (или мостом).

Теорема 5. Ребро является перешейком в том и только том случае, если

через него не проходит никакой цикл.

Доказательство. Если через ребро (a,b) проходит цикл, то после удаления этого ребра вершины a и b останутся соединимыми, значит, число компонент связности не увеличится. Обратно, если после удаления ребра (a,b)

число компонент связности не увеличивается, то вершины a и b останутся в одной компоненте, то есть существует соединяющий их маршрут, не проходящий через это ребро. По свойству 1 в нем имеется простой путь x1, x2,…, xn, соединяющий a и b, но тогда x1, x2,…, xn, x1– цикл, проходящий через (a,b). ■

Пусть G – ориентированный граф. В орграфе последовательность ребер,

в которой конец каждой дуги совпадает с началом следующей, называется

путем (в нем ребра проходят по их ориентации). Путь называется

ориентированной цепью, если каждое ребро встречается в нем не более одного раза, и простой ор-цепью, если каждая вершина инцидентна не более чем двум его ребрам. Контур – замкнутый путь в орграфе.

Если в ориентированном графе нельзя «пройти» от одной вершины до другой вершины, то расстояние между ними называют бесконечным.

143

Пусть vi и v j – вершины орграфа G. Вершина vi достижима из v j ,

если существует путь с началом vi и концом v j . Любая вершина достижима сама из себя. Вершины vi и v j сильно связаны, если они достижимы одна из другой.

Например, для графа, изображенного на рисунке 3.49, вершины v2 и v3

сильно связаны, вершины v1 и v4 сильно связаны, вершина v6 достижима из v1, но вершина v1 недостижима из v6 .

Рис. 3.49.

Орграф называется связным, если он связен без учета ориентации дуг, и

сильно связным, если из любой вершины vi в любую вершину v j существует путь. Компонентой сильной связности ориентированного графа называется максимальное множество вершин, в котором существуют пути (маршруты) из любой вершины в любую другую.

Граф, изображенный на рисунке. 3.50,

имеет три компоненты сильной связности. Они обведены пунктирными линиями.

Рис. 3.50.

Заметим, что существуют дуги, не принадлежащие ни одной из компонент сильной связности.

Достижимость в графе описывается матрицей достижимости

R=[rij], i, j=1, 2, ... n, где n – число вершин графа, а каждый элемент определяется следующим образом:

Матрица сильной связности ориентированного графа G − квадратная

матрица S(G)=[sij] порядка n, элементы которой равны 1 или 0:

Матрица достижимости несет важную информацию об ориентированном

графе. Ее анализ позволяет найти сильные компоненты графа, в которые входят взаимно достижимые вершины. Для двух таких вершин с номерами i и j должно выполняться равенство rij=rji=1. Поэтому, чтобы найти сильную компоненту, в

которую входит i-я вершина орграфа, нужно просмотреть i-ю строку и i-й

столбец матрицы R и сформировать множество Рi = {j : rij = rji = 1 номеров вершин, порождающих искомую сильную компоненту. Из определения матрицы достижимости вытекает, что в Рi содержатся номера всех вершин данной сильной компоненты. Поскольку две различные сильные компоненты

не пересекаются, множества Рi с номерами их вершин при поиске других

сильных компонент исключаются из рассмотрения. Процесс поиска начинается с произвольной вершины и заканчивается, когда для каждой вершины будет найдена содержащая ее сильная компонента. Может оказаться, что некоторые

(а может быть и все) сильные компоненты содержат только по одной вершине,

поскольку каждая вершина, по определению, достижима сама из себя.

Пример 3.20. Пусть матрица достижимости графа имеет вид:

145

В соответствии с описанной выше процедурой поиск сильных компонент

приведет к следующим результатам: Р1 = {xi }, Р2 = {x2 , x3}, Р3 = {x4 , x5},

Р4 = {x6 , x7 }.

Пример 3.21.

Определение связности, достижимости и расстояний на графе по

матрице смежности.

Пусть G – помеченный граф, V = {1, 2,…, n} и S(G )– матрица смежности графа G. Умножим матрицу S(G) на себя. Элемент sij2 квадрата матрицы смежности – это есть число маршрутов длины 2, соединяющих вершину vi с

вершиной v j .

Диагональные элементы матрицы S 2 , в частности, совпадают со степенями соответствующих вершин. Точно так же можно показать, что

146

элементы матрицы S 3 – это количество маршрутов длины 3, соединяющие соответствующие пары вершин; элементы S 4 – количество маршрутов длины

4, и т. д.

Таким образом, расстояние между вершинами vi и v j равно наименьшей

степени r матрицы S(G) такой, что (i,j)– элемент матрицы S r отличен от 0. Так как расстояния не могут быть больше n-1, где n – порядок графа, то для того,

чтобы найти все расстояния и выяснить другие связанные с ними вопросы,

достаточно рассмотреть степени r ≤ n-1. Если sij2 = 0 для всех 1 ≤ r ≤ n-1, то не существует маршрута между вершинами i и j, и граф не связан.

Некоторое ребро неориентированного графа называется перешейком,

если при его удалении число компонентных связностей увеличивается на единицу. Перешеек не может входить в цикл.

Разрез − множество ребер, удаление которого делает граф несвязным.

Ребро называется тупиком, если степень одной из инцидентных ему

вершин равна единице.

Вершина является шарниром, если ее удаление вместе с инцидентными ребрами увеличивает количество компонент связности.

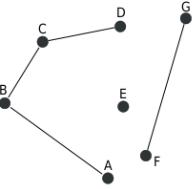
Пример 3.22. Определим шарниры в графе на рисунке 3.53.

Рис. 3.53.

147

Граф на рис. 3.53 связный, то есть представляет собой одну компоненту связности. Удалим вершину 2 вместе с инцидентными ребрами (строку 2 и

столбцы 3, 4, 5 в матрице инцидентности). В графе останутся три ребра: 13, 15

и 46. Ребра 13 и 15 образуют одну компоненту связности, а ребро 46 – другую.

Удаление вершины 2 увеличило количество компонент связности, поэтому вершина 2 является шарниром в графе.

Алгоритм связности.

Пусть G = (V , E) – граф. Алгоритм предназначен для вычисления значения c = c(G) – числа компонент связности графа G .

begin

V ′ := V ;

c := 0 $

while V ′ ¹ Æ do begin

Выбрать y ÎV ′ ;

Найти все вершины, соединенные маршрутом с у;

Удалить вершину у из V ′ и соответствующие ребра из E ;

c := c + 1;

end

end

Пример. 3.23. Применим алгоритм для графа на рис. 3.54.

Рис.3.54.

148

Граф на рис. 3.54. имеет три компоненты связности. Результаты поиска

представлены в таблице

Расстоянием между двумя вершинами графа называется длина кратчайшего пути, соединяющего эти вершины. Расстояние между вершинами a и b обозначается через d (a,b). Если в графе нет маршрута или пути,

соединяющего a и b, то есть эти вершины принадлежат разным компонентам

связности, то расстояние между ними считается бесконечным.

Расстояние от данной вершины a до наиболее удаленной от нее вершины называется эксцентриситетом вершины a и обозначается через e(a). Таким

образом, e(a) = max d (a, x).

x VG

Вершину с наименьшим эксцентриситетом называют центральной, а

вершину с наибольшим – периферийной. Множество всех центральных

вершин называется центром графа. Сама величина наименьшего эксцентриситета называется радиусом графа и обозначается через r(G), а

имеет полный граф, его диаметр равен 1. Среди связных графов с n вершинами наибольший диаметр, равный n −1, имеет цепь Pn .

Пример 3.24. Для графа G, изображенного на рисунке 3.55, найдем

радиус, диаметр и центры.

149

Рис. 3.55.

Решение. Чтобы определить центры, радиус, диаметр графа G, найдем

матрицу D(G) расстояний между вершинами графа, элементами dij которой

Заметим, что матрица D(G) симметрична относительно главной диагонали. С помощью полученной матрицы для каждой вершины графа G

Рис.3.56

Центр графа (рис. 3.56) составляют вершины 4, 6, 7; периферийные вершины – 1, 5 и 9; радиус его равен 3, а диаметр 5.