9957

110

Для любого н-графа матрица смежности симметрична относительно главной диагонали. Если граф не имеет петель, то на главной диагонали стоят все нули.

Свойства матрицы смежности для ор-графа:

1.Сумма единиц по строке определяет полустепень исхода;

2.Сумма единиц по столбцу определяет полустепень захода;

3.Сумма единиц по строкам и по столбцам определяет степень вершин.

Список ребер является более компактным описанием графа. Для всех трех графов он одинаков. Для н-графов G1 и G2 порядок вершин может быть произвольным, для ор-графа сначала указывается начало дуги, потом конец.

Пусть G – неориентированный граф.

Степень вершины (англ. degree, также валентность, англ. valency) в

теории графов – количество рёбер графа G, инцидентных вершине x. При

подсчёте степени ребро-петля учитывается дважды. Степень вершины обозначается как d(x) или deg(x). Максимальная и минимальная степень вершин графа G обозначаются соответственно (G) и δ(G).

Набор степеней графа – это последовательность степеней его вершин,

выписанных в неубывающем порядке.

Вершина степени 0 называется изолированной, вершина степени 1

называется висячей (или концевой) вершиной.

Вершина называется нечетной, если ее степень – число нечетное.

Вершина называется четной, если ее степень – число четное.

111

Набор степеней графа на рис. 3.21: (1, 3, 6, 8).

Максимальная степень равна (G)=8, минимальная δ(G)=1. Чётное число вершин (две вершины: u, z)

данного графа имеют нечётную степень. Сумма степеней всех вершин равна 18, то есть равна удвоенному числу рёбер графа.

Теорема 1. Сумма степеней всех вершин графа с n вершинами равна

n

удвоенному числу m его ребер: ∑ deg(vi ) = 2m .

i =1

Доказательство: Подсчет всех степеней вершин графа можно вести по вершинам. Возьмем пустой граф. Сумма степеней вершин такого графа равна нулю. При добавлении ребра, связывающего любые две вершины, сумма всех степеней увеличивается на 2 единицы. Таким образом, сумма всех степеней вершин четна и равна удвоенному числу ребер.■

Из этой теоремы следует, что каждый граф имеет чётное число нечётных вершин.

Терема 2. (Лемма о рукопожатиях)1. Любой конечный неориентированный граф имеет чётное число вершин нечётных степеней.

Доказательство: Обозначим через ∑1 и ∑2 – количество всех вершин графа, имеющих нечетную и четную степень соответственно. По теореме 1 ∑1+ ∑2 = 2m , следовательно, ∑1 = 2m − ∑2 . Правая часть этого соотношения четна, поэтому четна и левая часть.■

Если все вершины графа имеют одинаковую степень k, граф называют k-

регулярным или регулярным графом степени k. В этом случае сам граф имеет степень k. Примерами регулярных графов являются правильные

1 Лемма о рукопожатиях берёт название от популярной аналогии: в группе людей, некоторые из которых пожимают друг другу руки, чётное число людей поприветствовало таким образом нечётное число коллег.

112

многогранники: куб, октаэдр и т.д. Из теоремы 1 следует, что в регулярном

графе степени k число ребер kn .

2

Пример 3.9. Александр, Борис, Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?

Решение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени (см.

рисунок 3.22), а производимому рукопожатию соответствует отрезок или часть кривой, соединяющие конкретные точки – имена.

Рис. 3.22. а) нулевой граф с пятью вершинами; б) неполный граф с пятью вершинами

Рассмотрим процесс соединения точек А, Б, В, Г, Д ребрами.

1. Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рис. 3.22 a). Такая схема, состоящая из «изолированных» вершин, называется

нулевым графом.

2. Ситуация, когда совершены еще не все рукопожатия, может схематически быть изображена, например, с помощью рисунке 3.22 b): пожали руки А и Б, А и Г, Д и Г, В и Д. Следующий момент, когда добавятся,

например, пожатия рук А и В, Г и Б. Графы, в которых не построены все возможные ребра, называются неполными графами.

3. На рисунке 3.23 изображен граф, соответствующий всем совершенным рукопожатиям. Этот граф является полным графом.

113

Рис. 3.23. Полный граф с пятью вершинами.

Если подсчитать число ребер графа, изображенного на рисунке 3.23, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Всего их 10.

Пример 3.10. Доказать, что число зрителей, пришедших на стадион смотреть футбольный матч и имеющих нечетное число знакомых (среди того же множества зрителей), четно.

На языке теории графов имеем нечетные вершины. Нужно доказать, что их четное количество, а это доказано в теореме 2.

Пример 3.11. В кабинете 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?

Решение. Предположим, что это возможно. Рассмотрим тогда граф,

вершины которого соответствуют телефонам, а ребра – соединяющим их проводам. В этом графе 15 вершин, степень каждой из которых равна пяти.

Подсчитаем количество ребер в этом графе. Для этого сначала просуммируем степени всех его вершин. Ясно, что при таком подсчете каждое ребро учтено дважды (оно ведь соединяет две вершины). Поэтому число ребер графа должно быть равно 15·5/2, но это число нецелое, следовательно, такого графа не существует, а значит, и соединить телефоны требуемым образом невозможно.

При решении этой задачи мы выяснили, как подсчитать число ребер графа, зная степени всех его вершин. Для этого нужно просуммировать степени вершин и полученный результат разделить на два.

Ответ: соединить телефоны требуемым образом невозможно.

115

Задачи.

1.Изобразить неориентированный граф, удовлетворяющий условиям:

1)число вершин n>6;

2)число ребер m >9.

Составить матрицу смежности, соответствующую данному графу.

2.Изобразить орграф, удовлетворяющий условиям:

1)число вершин n>8;

2)число дуг m>10.

Составить матрицу инцидентности, соответствующую данному графу.

3.Для графов, изображенных на рисунке 3.24 и 3.25, составить матрицы смежности и инцидентности.

Рис. 3.24

Рис.3.25.

4.Задайте разными способами граф на рис. 3.26. Является ли бинарное отношение, соответствующее заданному орграфу, рефлексивным,

антирефлексивным, симметричным, антисимметричным, транзитивным?

Рис. 3.26.

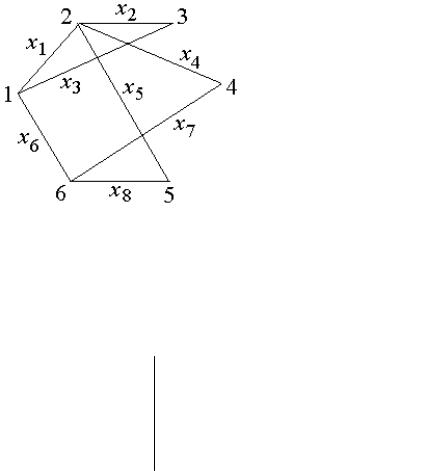
5. По матрице инцидентности определите степени вершин:

7. Составьте для каждого из графов G и H (рис.3.27) множества вершин и ребер. Задайте графы G и H матрицами инцидентности и смежности, а также списком ребер:

G H

Рис.3.27.

8. По матрице инцидентности нарисуйте граф. Составьте список его вершин и

ребер, а также матрицу смежности.

x1 x2 x3 x4 x5 x6 x7

117

10. Даны орграфы (рис. 3.28 – 3.29). Составьте для каждого из них матрицу смежности, матрицу инцидентности, матрицу достижимости. Каковы максимальная полустепень исхода и минимальная полустепень захода в этих орграфах? Являются ли эти орграфы направленными? Есть ли в них источники или стоки?

Рис. 3.29

Рис. 3.28.

11.Являются ли бинарные отношения, соответствующие орграфам из

антисимметричными, транзитивными?

12.Какое бинарное отношение соответствует: а) неориентированному псевдографу без кратных ребер; б) турниру?

13.Найдется ли граф с пятью вершинами, у которого одна вершина изолированная, а другая степени 4?

14.Изобразите граф с пятью вершинами, у которого две вершины имеют одинаковую степень?

15.Если в графе с пятью вершинами ровно две вершины имеют одинаковую степень, то могут ли они быть обе изолированными или иметь степень 4?

16.Верно ли, что в полном орграфе всегда существует источник?

118

17.Орграф задан матрицей инцидентности, в которой строки соответствуют

18.Нарисуйте граф с пятью вершинами, который: а) имеет два стока и один источник; б) не имеет ни стока, ни источника.

19.Сколько рёбер имеет полный граф с p вершинами?

20.Постройте полный граф с 10-ю ребрами.

21.Постройте граф отношения «а делит в» (а|b) для множества чисел от 1 до

20.Является ли бинарное отношение, соответствующее построенному графу,

рефлексивным, антирефлексивным, симметричным, антисимметричным,

транзитивным?

22. При каких n существуют графы с n вершинами, каждая из которых имеет:

а) степень 3? ; б) степень 4?

23. Постройте граф (если он существует) с последовательностью степеней:

а) (4, 3, 3, 2, 2); б) (5, 4, 2, 2, 1); в) (3, 3, 2); г) (3, 2, 2, 1).

24.Постройте орграф, для которого последовательность (3, 3, 3, 2, 2) является как списком полустепеней исхода вершин, так и списком полустепеней захода.

25.Сколько вершин может быть у графа с 4 ребрами, если петли, кратные ребра и изолированные вершины у него отсутствуют?

26.Сколько рёбер может быть у регулярного графа с 9 вершинами?

27.Сколько рёбер имеет регулярный граф с p вершинами степени r?

119

28. Существуют ли графы со следующими наборами степеней вершин:

а) {2, 3, 3, 2, 3}; б) {1, 2, 3, 4}? Если существуют, то изобразите их графически. 29. Покажите, что простой граф, имеющий, по крайней мере, две вершины,

содержит две вершины одинаковой степени. 30. Являются ли следующие графы планарными?

31. Проверьте формулу Эйлера для следующих графов:

32.В студенческой группе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этой группе), 11 по 4, а 10 по 5 друзей?

33.Семеро студентов, разъезжаясь на каникулы, договорились, что каждый пошлет электронное письмо трем остальным. Может ли оказаться, что каждый получит письма от тех, кому написал сам?

34.В государстве 100 городов, из каждого выходит по 4 дороги. Сколько всего дорог в государстве?