
9286
.pdf
y
2 |
x |
|
|
|
|
|
Решение x 2, y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Положим (x) = [ max { 0, g(x)} ]2 |
0, если x 2 |
|
||||
, тогда (x) = |
( - x + 2) 2 , если |
. |
||||
|
|
|
x 2 |
|||
Минимум f (x) + * (x) |
достигается в точке |
1 |
. При |
последова- |
||
2 - |
|
|||||
2 * |
||||||
тельность таких точек стремиться к точке x = 2, являющейся точкой минимума ис-
ходной задачи.
График:
2 *
2 1.5
1 * |
1 0.5 |
f 2 *
f 1 *
0 |
2 |
Алгоритм метода штрафных функций. f (x) min
---
gi (x) 0, i = 1,m
81
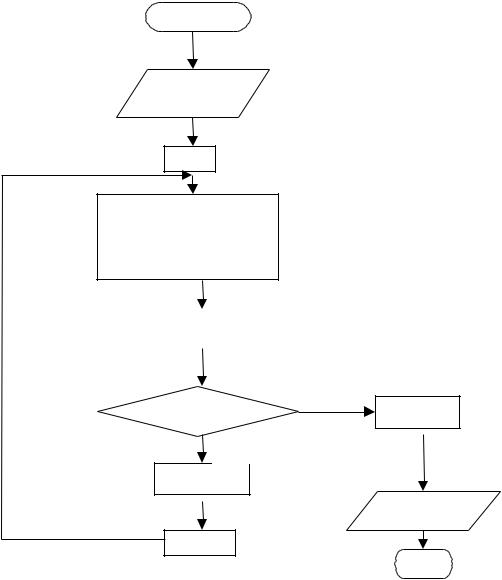
---
h j (x) = 0, j = 1, l
x R n
начало
Ввод
, x 1 , 1 ,
Ре шить задачу безусловной
minоптимизации(f( x ) ( x ))
k
x *
и найти ее ре шение |
. |
|
|
|
|
|
|
|
нет
Вывод
конец
– точность вычисления;
– некое число, 1;
x1 – начальная точка;
1 – штрафной параметр, 1 0 ; k – параметр цикла;
x* – оптимальное решение задачи безусловной оптимизации (на каждой итера-
ции свое);
82
x ** – оптимальное решение исходной задачи.
83
Метод барьерных функций или метод внутренних штрафных функций.
В этом методе к целевой функции исходной задачи добавляется барьерная функция, которая не позволяет генерируемым точкам выходить за пределы допу-
стимой области. Эта последовательность точек сходится к оптимальному решению исходной задачи.
Барьерные функции используются, также, как и штрафные, для преобразования задачи с ограничениями в задачу безусловной оптимизации или в последователь-
ность таких задач. Барьерные функции как бы препятствуют выходу из допустимой области. Ограничения должны быть только в форме неравенств.
Исходная задача f (x) min
gi (x) 0 , i 1,...,m x R n
преобразуется в задачу безусловной оптимизации:
f1(x) f (x) * B( x) min, |
x R n , |
0 , |
где B(x) – барьерная функция, которая в общем виде записывается как:
m
B(x) 1(gi (x)) , i 1
где 1 – функция одной переменной, удовлетворяющая условиям:
1( y) 0, если y 0 и lim 1( y) .
y 0
B(x) конструируется таким образом, чтобы она была неотрицательна и непре-
рывна в области { x : gi (x) 0} и стремилась к бесконечности при приближении из внутренней точки к границе области.
|
m |
( 1) |
|
Типичная барьерная функция имеет вид: |
B( x) |
|
(«минус», так как зада- |
|
|||
|
i 1gi (x) |
|
|
ча на min и gi (x) 0 ).
Функцию f (x) B( x) называют вспомогательной конструкцией.
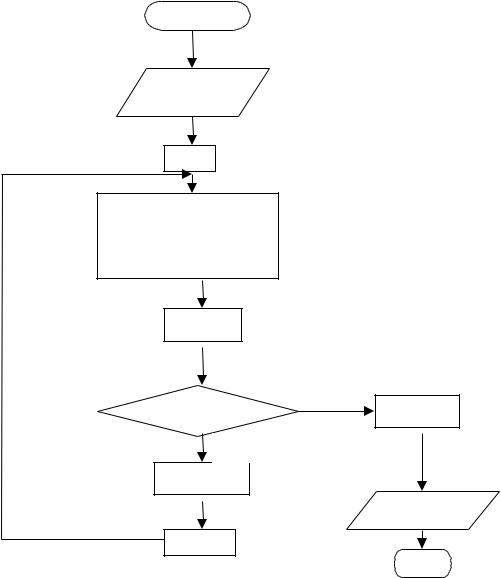
Алгоритм метода барьеров. f (x) min
---
gi (x) 0, i = 1, m
x R n
начало
Ввод
, x1 , 1 ,
k 1
Ре шить задачу безусловной
оптимизации
f ( x ) k * B(x)
и найти ее ре шение x* .
xk 1 x*
kB( xk 1 )
нет
k 1 k
k k 1
x** xk 1
Вывод x**
конец
– точность вычисления; k – параметр цикла;
– некое число, (0,1) ;
x1 – начальная точка;
1 – штрафной параметр, 1 0 ;
x* – оптимальное решение задачи безусловной оптимизации (на каждой итера-
85
ции свое); x** – оптимальное решение исходной задачи.
2.4 Контрольные вопросы
Контрольные вопросы к разделу 1 «Оптимизационные задачи нелинейного
программирования. Их классификация»
1.Привести примеры оптимизационных нелинейных задач в науке,
производстве и экономике.
2.Формулировка задач нелинейного программирования и их классификация.
3.Унимодальные функции. Выпуклые функции. Геометрический смысл выпуклости функции.
4.Как проверить, является ли функция выпуклой или вогнутой.
5.Глобальный и локальный максимум (минимум). Методы нахождения.
6.Пусть данная точка удовлетворяет достаточным условиям существования локального минимума. Как установить, является ли этот минимум глобальным.
7.Приведите алгоритм определения глобального оптимума.
Контрольные вопросы к разделу 2 «Безусловная нелинейная оптимизация
функций одной переменной. Классификация методов».
1.Точный метод поиска экстремума функции одной переменной.
2.Одномерная минимизация функций. Прямые методы: перебора, поразрядного поиска и дихотомии
3.Метод сканирования
a)Экстремум каких функций можно найти методом сканирования?
b)Основное достоинство метода сканирования.
c)Способ «размещения» точек вычисления критерия оптимальности на оси Х.
d)Каким образом повысить точность нахождения решения?
e)Условие отыскания оптимального решения.
4.Метод деления пополам
86
a)Для каких функций пригоден метод половинного деления?
b)Каково основное достоинство метода половинного деления?
c)Каким образом повысить точность нахождения решения Х*?
d)Условие отыскания оптимального решения.
e)Всегда ли метод гарантированно дает решение?
f)Каким образом определяется следующий отрезок, на котором находится экс-
тремум?
5.Одномерная минимизация функций. Метод золотого сечения.
a)Всегда ли метод гарантированно дает решение?
b)Как влияет вид функции на процесс нахождения решения?
c)Каким образом определяется следующий отрезок, на котором находится экс-
тремум?
d)Основное достоинство метода золотого сечения.
e)Каким образом повысить точность нахождения решения?
f)Что делится по правилу золотого сечения?
g)Сколько раз нужно вычислить значение функции на каждом шаге?
6.Одномерная минимизация функций. Метод средней точки и метод хорд.
7.Одномерная минимизация функций. Метод Ньютона.
a)Условие окончания поиска.
b)Каким образом повысить точность нахождения решения?
c)Всегда ли метод гарантированно дает решение?
d)Возможно ли нахождение решения задачи оптимизации за один шаг?
e)Как влияет вид функции на процесс нахождения решения?
Контрольные вопросы к разделу 3 «Безусловная оптимизация функции
многих переменных».
1.Квадратичные формы и их типы. Градиент и его геометрический смысл.
2.Классические (точные) методы безусловной оптимизации функции многих переменных. Критерий Сильвестра проверки достаточных условий экстрему-
ма.
87
3.Классические (точные) методы безусловной оптимизации функции многих переменных. Формулировка способа проверки условий экстремума функции многих переменных через собственные значения матрицы Гессе.
4.Главные отличительные признаки методов второго порядка от методов перво-
го и нулевого порядков.
5.Численные методы безусловной оптимизации функции многих переменных.
Классификация методов. Итерационный процесс поиска минимума. Исчерпы-
вающий спуск.
6.Численные методы нулевого порядка безусловной оптимизации функции мно-
гих переменных. Метод покоординатного спуска.
7.Численные методы первого порядка безусловной оптимизации функции мно-
гих переменных. Метод наискорейшего спуска.
8.Численные методы второго порядка безусловной оптимизации функции мно-
гих переменных. Метод Ньютона.
9.Отличия метода Ньютона от метода Ньютона-Рафсона и от метода Марквард-
та.
Контрольные вопросы к разделу 4 «Условная оптимизация функции
многих переменных».
1.Общая постановка задачи динамического программирования. Условия применимости. Проблемы реализации. Примеры.
2.Классические методы условной оптимизации функции многих переменных в задачах с ограничениями-равенствами. Метод Лагранжа
3.Классические методы условной оптимизации функции многих переменных в задачах с ограничениями-неравенствами.
4.Численные методы поиска условного экстремума функции многих переменных.
5.Проблемы овражности и проблемы реализации.
88
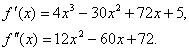
3. Методические указания по подготовке к практическим занятиям
3.1Общие рекомендации по подготовке к практическим занятиям
Входе подготовки к практическим занятиям необходимо изучать основную литературу, познакомиться с дополнительной литературой. При этом необходимо учесть рекомендации преподавателя и требования учебной программы.
Всоответствии с этими рекомендациями и подготовкой полезно дорабатывать свои конспекты лекции, делая в нем соответствующие записи из литературы,
рекомендованной преподавателем и предусмотренной учебной программой.
Целесообразно также подготовить тезисы для возможных выступлений по всем учебным вопросам, выносимым на практическое занятие.
При подготовке к занятиям можно также подготовить краткие конспекты по вопросам темы. Очень эффективным приемом является составление схем и презентаций.
Готовясь к докладу или реферативному сообщению, желательно обращаться за методической помощью к преподавателю. Составить план-конспект своего выступления. Продумать примеры с целью обеспечения тесной связи изучаемой теории с реальной жизнью. Своевременное и качественное выполнение самостоятельной работы базируется на соблюдении настоящих рекомендаций и изучении рекомендованной литературы.
3.2 Примеры задач для практических занятий
Задачи для раздела 1.
Задача 1.
Показать, что функция 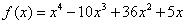 унимодальна на отрезке [3; 5].
унимодальна на отрезке [3; 5].
Решение. Найдем последовательно первую и вторую производные функции
Решим уравнение  . Корни полученного квадратного трехчлена х1=2 и
. Корни полученного квадратного трехчлена х1=2 и
х2=3. Следовательно,  и, в частности, при х [3; 5]. Используя
и, в частности, при х [3; 5]. Используя
89
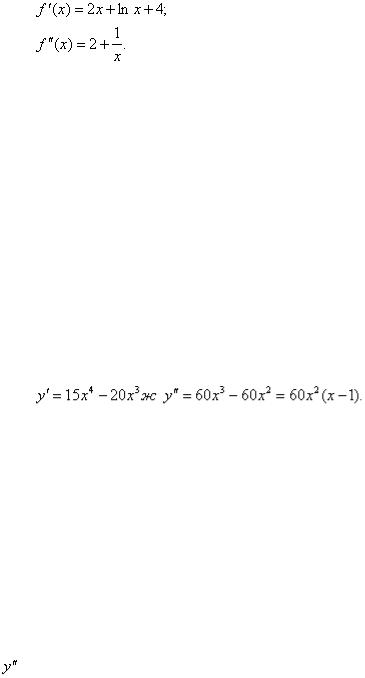
дифференциальный критерий унимодальности, получаем, что f(x) выпуклая на от-
резке [3; 5] и, значит, унимодальная.
Задача 2.
Выяснить, является ли функция f(x)=х2-3х+хlnx на отрезке [1;2] унимодальной.
Решение. Найдем первую и вторую производные функции:
Решим уравнение  . Полученное уравнение имеет единственный корень x=-0,5. Следовательно,
. Полученное уравнение имеет единственный корень x=-0,5. Следовательно, 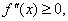 . Если x-0,5 и, в частности, при x [1; 2]. Используя дифференциальный критерий унимодальности, получаем, что f(x) выпуклая на от-
. Если x-0,5 и, в частности, при x [1; 2]. Используя дифференциальный критерий унимодальности, получаем, что f(x) выпуклая на от-
резке [1; 2] и, значит, унимодальная.
Задача 3.
Определить направление выпуклости и точки перегиба кривой 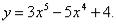
Решение. Ищем точки х, в которых  или не существует, а кривая непре-
или не существует, а кривая непре-
рывна и которые лежат внутри области расположения кривой:
 в точках х = 0, х = 1. Эти точки являются искомыми, так как область рас-
в точках х = 0, х = 1. Эти точки являются искомыми, так как область рас-
положения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как 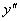 суще-
суще-
ствует всюду.
Исследуем найденные точки, определяя знак второй производной слева и спра-
ва от каждой из них. Запишем это исследование в таблице:
х |
-1 |
0 |
1/2 |
1 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
0 |
- |
0 |
+ |
|
|
|
|
|
|
у |
Выпукла |
Нет перегиба |
Выпукла |
Перегиб |
Вогнута |
|
|
|
|
|
|
|
|
|
|
|
|
Из таблицы следует, что х= 1 есть абсцисса точки перегиба кривой: у(1) = 2.
Поскольку эта кривая непрерывная, то во всем интервале (- , 1) она выпукла, а во
90
