
9286
.pdf
Рис. 13. Блок-схема метода дихотомии.
Пометим индексами номер шага.
ai – левый конец отрезка неопределенности при i- й итерации.
bi – соответственно правый конец |
|
|
|
|||||
Тогда b1 a1 |
b a |
|
согласно описанию I-го шага |
|||||
|
||||||||
|
|
|
2 |
|
2 |
|
|
|
b2 a2 |
b1 a1 |
|
|
(b a) / 2 / 2 |
|
|
(b a ) / 4 / 2 |
|
|
|
|
||||||
2 |
|
2 |
|
2 |
|
2 |
|
|
(b a ) / 4 (b a ) / 22
По математической индукции предположим, что bk a k (b a ) / 2k
Рассмотрим bk 1 a k 1:
31
bk 1 a k 1 (bk a k ) / 2 / 2 |
(b a ) / 2k |
|
(b a ) / 2k 1 |
|
||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|||
Таким образом, методом математической индукции доказали, что после выпол- |
||||||||||||||||
нения k-го шага метода дихотомии b k a k |
|
(b a ) |
. |
|
|
|
||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2k |
|
|
|
|
|
|
|
Поскольку задача решается с точностью , то необходимое число шагов метода |
||||||||||||||||
должно удовлетворять неравенству: (b a ) / 2k или |
|
|
|
|||||||||||||
|
(b a ) |
|
2k > |
b - a - |
|
k log |
|
b a |
. |
|
||||||
|
|
- |
2 |
|
|
|||||||||||
2 |
k |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, заранее по постановке задачи мы можем узнать число шагов
метода.
Замечание 1. Из последней оценки видим, что число шагов метода не зависит от вида f (x) .
Замечание 2. Этот метод можно применять для минимизации функций, не яв-
ляющихся унимодальными, однако, без гарантии, что будет найден обязательно глобальный минимум.
Пример. Методом дихотомии найти минимум f (x) x 2 на отрезке [ 1,1] c0,05.
Решение.
Предварительно оценим, сколько шагов для этого потребуется.
Выберем 0,02 .
k log 2 ((2 0,02) / 0,03) 6,05.
Поскольку k –целое, то потребуется 7 шагов. Осуществим их.
1-й шаг.
x |
|
1 1 |
|
|
0,01 0,01 |
|
|
|
|||
|
|
|
|
|
|||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
|
1 1 |
0,01 0,01 |
|
|
|
|||||
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
f (x ) f (x |
2 |
) a1 = x |
1 |
= -0,01; b1 |
= 1. |
||||||
|
1 |
|
|
|
|
|
|
|
|
||
32
2-й шаг.
x1 0,485; x2 0,505
f (x ) f (x |
2 |
) a 2 |
= -0,01; b2 |
= 0,505. |
1 |
|
|
|
3-й шаг.
x1 0,2375; x2 0,2575
f (x ) f (x |
2 |
) a 3 |
= -0,01; b3 |
= 0,2575. |
1 |
|
|
|
4-й шаг.
x1 0,10375; x2 0,12375
f (x ) f (x |
2 |
) a 4 |
= -0,01; b4 = 0,12375. |
1 |
|
|
5-й шаг.
x1 0,051375 ; x2 0,071375
f (x ) f (x |
2 |
) |
a 5 = -0,01; |
b5 |
= 0,071375. |
|
1 |
|
|
|
|
|
|
6-й шаг. |
|
|
|
|
|
|
x1 0,0206875; x2 0,0406875 . |
|
|||||
f (x ) f (x |
2 |
) |
a6 = -0,01; |
b6 |
= 0,0406875 |
|
1 |
|
|
|
|
||
7-й шаг.
x1 0,005344 ; x2 0,025344
f (x ) f (x |
2 |
) a 7 |
= -0,01; b7 |
= 0,025344 . |
1 |
|
|
|
b7 a 7 0,035344 0,05
b6 a 6 0,0506875 0,05
Следовательно, действительно, только 7 шагов приводят к решению с заданной
точностью. В качестве x* принимаем –0,01.
На следующем рисунке проиллюстрировано уменьшение отрезка неопределен-
ности по шагам.
33

-1 |
|
|
1 |
-0,01 |
|
1 |
1-й шаг |
-0,01 |
0,505 |
|
2-й шаг |
-0.01 |
0,2575 |
|
3-й шаг |
-0,01 |
0,12375 |
|
4-й шаг |
-0,01 |
0,071375 |
|
5-й шаг |
-0,01 |
0,0406875 |
|
6-й шаг |
Рис. 14. Пошаговое уменьшение отрезка неопределенности.
Метод золотого сечения.
Метод золотого сечения также является последовательным методом миними-
зации. Опираясь на свойства золотого сечения отрезка, этот метод использует найденные значения F(X) более рационально, чем метод деления отрезка пополам,
что позволяет переходить к очередному отрезку, содержащему точку Х* после вы-
числения одного, а не двух значений F(X).
Метод основан на делении текущего отрезка [a; b], где содержится искомый экстремум, на две неравные части, подчиняющиеся правилу золотого сечения, для
определения следующего отрезка, содержащего максимум.
Правило золотого сечения: отношение всего отрезка к большей его части
равно отношению большей части отрезка к меньшей.
Рассмотрим следующую задачу. Возьмем отрезок [a,b] , найдем внутри этого
отрезка x1, x2 |
(x1 < x 2 ) , образующие золотое сечение. |
x1 |
x2 |
a |
b |
Для этого необходимо выполнение следующих условий:
x2 a |
|
b x1 |
|
x1 a |
|
b x2 |
|
1 |
|||
b a |
b a |
x |
2 |
a |
b x |
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|||
34

Найдем , при котором возможны равенства
|
x2 a |
|
|
1 |
|
|
|
|
x2 = a + (b - a) * |
|
1 |
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
b a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
b x1 |
|
|
1 |
|
|
|
x = b - (b - a) * |
1 |
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
b a |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b (b a) * |
1 |
|
|
a |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x1 a |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|||||||
|
x2 a |
|
|
a |
(b a) * |
1 |
|
|
a |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
(b a) * (1 |
1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 |
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||
|
(b a) * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 1 0, |
|
|
|
= |
1 |
|
1 |
|
|
|
1 |
1 5 |
|
||||||||||||||||||||||||||||||||
|
1,2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Поскольку 0 |
|
|
= |
1 + |
|
|
|
5 |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Метод золотого сечения состоит в том, что начиная с 1-го шага отрезок делится |
|||||||||||||||||||||||||||||||||||||||||||||
точками x1, |
x2 |
в пропорции золотого сечения: |
|||||||||||||||||||||||||||||||||||||||||||
При каждом шаге отрезок неопределенности уменьшается в раз.
b1 a1 b a
............................
b N a N b a
N
Если – заданная точность, то число шагов метода золотого сечения следует
|
|
|
|
|
|
ln( |
b - a |
) |
|
|
b a |
|
|
b a |
N > |
|
. |
||
находить как решение неравенства |
|
N |
|
||||||
N |
|
ln |
|
||||||
|
|
|
|
|
|
||||
Существуют аналитические формулы для расчета новой точки на отрезке, где
35
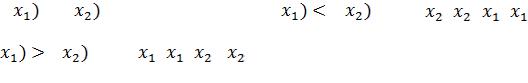
находится минимальное значение F(X).
При N шагах метода золотого сечения f (x) вычисляется N 1 раз, так как на
1-м шаге f (x) вычисляется дважды, а на последующих шагах по одному разу, при этом одна из внутренних точек отрезка неопределенности последующего шага сов-
падает с одной из точек предыдущего шага.
Метод золотого сечения обеспечивает более быструю сходимость к решению,
чем многие другие методы, и применим, очевидно, только для одноэкстремальных функций, т. е. функций, содержащих один экстремум того типа, который ищется в задаче.
Алгоритм:
1 шаг: Определить точки 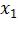 и
и 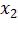 , принадлежащие отрезку [a;b] по формулам:
, принадлежащие отрезку [a;b] по формулам:
 = a+
= a+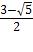 *(b-a) и
*(b-a) и  a+
a+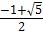 *(b-a)
*(b-a)
2 шаг: проверяем критерий останова. Вычисляем  :
: 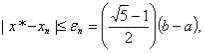 .
.
Если 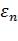 <
< , то СТОП, иначе – следующий шаг.
, то СТОП, иначе – следующий шаг.
3 шаг: Вычисляем f( |
и f( |
и сравниваем. Если f( |
f( , то b= , = , |
|
вычисляем. Если f( |
f( |
, то а= , = , |
вычисляем. |
|
4 шаг: переходим на 2 шаг. |
|
|
|
|
36
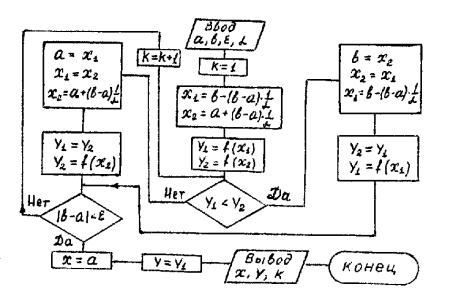
Рис. 15. Блок-схема метода золотого сечения.
Пример. Найти минимум f (x) x2 на отрезке [ 1,1] c 0,05.
Предварительно определим, сколько потребуется шагов метода золотого сече-
ния.
2 |
|
|
|
0,05 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(1,618) N |
|
|
|
|
|
|
|
|||||||||||||
|
|
ln( |
|
2 |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
N |
|
0,05 |
|
|
|
7,7 |
|
|
|
|
|
|
||||||||
|
ln 1,618 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Итак, |
потребуется 8 шагов |
метода |
золотого сечения, при этом значения |
||||||||||||||||||
f (x) придется вычислять 9 раз. |
|
|
|
|
|
|
|||||||||||||||
1-й шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x1 1 2 * |
|
|
|
|
1 |
|
0,2361; x2 |
1 |
|
2 |
0,2361 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1,618 |
|
|
1,618 |
|
||||||||||||
|
f (x ) f (x |
2 |
) |
|
a1 = -0,2361; |
b1 = 1. |
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2-й шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x 0,2361; |
x |
|
0,2361 |
1,2361 |
0,5279 |
|
||||||||||||||
|
2 |
|
|
||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
1,618 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f (x ) f (x |
2 |
) |
|
a 2 = -0,2361; |
|
b2 = 0,5279 . |
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
|
|
||

3-й шаг.
x |
0,5279 |
|
(0,5279 0,2361) |
0,05573 ; |
x |
|
|
|
0,2361 |
|||||||||||
|
|
|
|
2 |
||||||||||||||||
1 |
|
|
|
|
|
|
1,618 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x |
) f (x |
2 |
) |
a 3 = -0,2361; |
b3 = 0,2361. |
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4-й шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
0,2361 |
|
(0,2361 0,2361) |
0,05573; |
x |
|
|
0,05523 |
||||||||||||
|
|
|
2 |
|||||||||||||||||
1 |
|
|
|
|
|
|
1,618 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x |
) f (x |
2 |
) |
a 4 = -0,05573; |
b4 = 0,2361. |
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5-й шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
0,2361 |
(0,2361 0,05573) |
0,05573; |
x |
|
|
|
0,12463 |
||||||||||||
|
|
2 |
|
|||||||||||||||||
1 |
|
|
|
|
|
|
1,618 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x |
) f (x |
2 |
) |
a 5 = -0,05573; |
b5 = 0,12463. |
|
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6-й шаг. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
0,12463 |
(0,12463 0,05573) |
0,01316 ; |
|
x |
|
0,05573 |
|||||||||||||
|
|
2 |
||||||||||||||||||
1 |
|
|
|
|
|
|
1,618 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x1) f (x2 ) a 6 = -0,05573; 7-й шаг.
(0,05573 0,05573) x1 0,05573
1,618
f (x1) f (x2 ) a 7 = -0,05573; 8-й шаг.
x 0,01316 (0,01316 0,05573) |
|||
1 |
|
|
1,618 |
|
|
|
|
f (x ) f (x |
2 |
) a8 |
= -0,02942; |
1 |
|
|
|
b6 = 0,05573.
0,01316 ; x 2 0,01316
b7 = 0,01316 .
0,02942 ; x 2 0,01316
b8 = 0,01316.
b8 a8 |
0,04258 |
x* = - 0,02942 |
Сравнительная характеристика методов исключения интервалов:
38
Выше были рассмотрены примеры решения задач различными методами ис-
ключения интервалов. Еще раз подчеркнем, что эти методы пригодны для любых непрерывных одноэкстремальных функций (для метода половинного деление необ-
ходимо, чтобы функция не имела горизонтальных участков). Сходимость методов и их эффективность не зависят от свойств функции. Основное достоинство метода сканирования заключается в снижении количества повторов вычисления для реше-
ния с заданной погрешностью, но при этом повышается вероятность пропуска
«острого» глобального экстремума. Все три метода легко поддаются алгоритмиза-
ции. Для повышения точности нахождения решения необходимо просто уменьшить задаваемую погрешность. При сравнительном анализе можно сделать вывод, что метод золотого сечения оказывается более эффективным по сравнению с остальны-
ми двумя методами, поскольку он требует наименьшего числа оцениваний значения функции для достижения одной и той же заданной точности
Метод Ньютона
Метод Ньютона относится к методам 2-го порядка и рекомендуется к примене-
нию в том случае, когда задача минимизации достаточно хорошо локализована.
Обычно это имеет место в том случае, когда на начальном этапе применяется один из методов 0-го порядка, а затем осуществляется переход к методу Ньютона.
Для этого необходимым условием является гладкость f (x) , существование не рав-
ных нулю f (x) , f (x) , f (x) для x [a,b].
Тогда если xk – k-е приближение к точке минимума, то расчетной формулой
метода Ньютона будет формула xk 1 xk |
f (xk ) |
. |
|
f (xk ) |
|||
|
|
Метод Ньютона имеет высокую скорость сходимости:
| xk 1 x* | C *| xk x* |2
где x*– точка минимума; С – некоторая положительная константа.
Процесс вычисления продолжается до тех пор, пока не будет достигнуто
39

| xk 1 xk |
На следующем рисунке приведена блок-схема алгоритма.
Рис. 16. Блок – схема метода Ньютона.
Пример. Найти минимум f (x) (1 x) * sin x на отрезке [0,1] c точно-
стью 0,01.
Зададимся x0 , например, возьмем середину отрезка [0,1]:
Пусть x0 0,5
Для данного примера расчетной формулой метода Ньютона будет
xk 1 |
xk |
f (xk ) |
xk |
(1 xk ) * cos xk sin xk |
|
f (xk ) |
xk *sin xk 2 * cos xk |
||||
|
|
|
1-й шаг.
x1 0,5 (1 0,5) *cos 0,5 sin 0,5 0,47319 0,5*sin 0,5 2*cos 0,5
| x1 x0 | | 0,47319 0,5 | 0,0263 0,01
2й шаг.
x2 0,47319 (1 0,47319) * cos 0,47319 sin 0,47319 0,488169 0,5*sin 0,47319 2* cos 0,47319
| x2 x1 | | 0,48169 0,47139 | 0,0085 0,01
Ответ: x* 0,48 .
40
