
8658
.pdf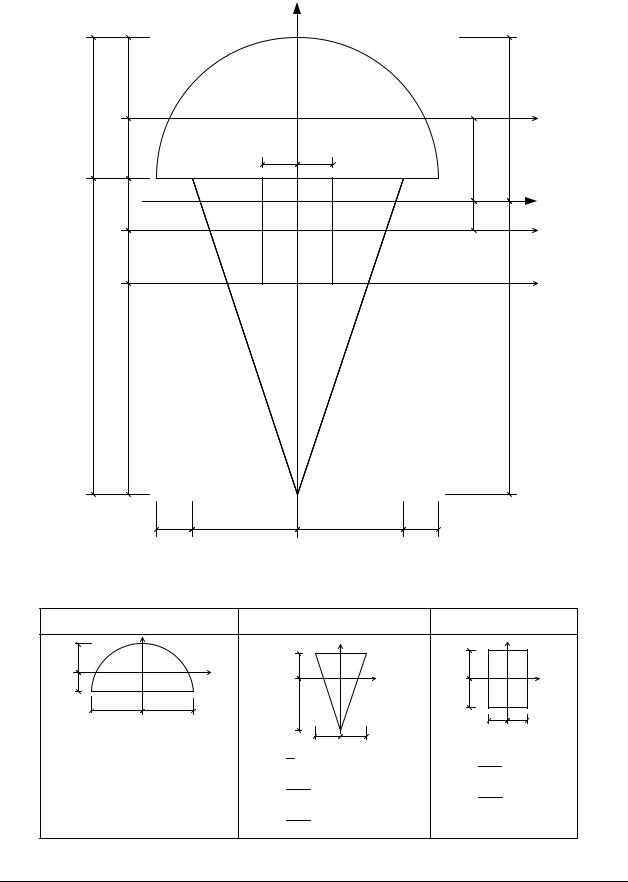
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
|
|
|
|
|
|
|
|
|
2.30 |
|
|
|
|
|
|
|
|
|
3.00 |
|
|
|
|
|
1.50 |
|
|
|
|
|
1.70 |
|
|
|
|
|
|
|
|
|
6.00 |
|
|
|
|
|
1.50 |
|
|
|
|
|
A1 = |
π 82 |
=25.13см |
2 |
|
|
|
|
|
|
|
|
|
A 3 = 2× 3 = 6см2 |
|
|||||||
8 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
=0.28 π 84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
J x1 |
=0.28×100.53см4 |
A 2 = |
2 ×6 |
× 9 = 27 cм2 |
|
|
Jx3 |
= 2×33 |
= 4.5 см4 |
||||||||||||
|
|
π 8 |
4 |
128 |
|
|
|
Jx2 |
= |
6×93 |
=121.5 см |
4 |
|
|
|
12 |
3 |
|
|
||
Jy1 |
= |
|
=100.53см |
4 |
36 |
|
|
|
|
Jy3 |
= |
3 ×2 |
|
=2см |
4 |
||||||
128 |
|
|
|
3 |
|
|
12 |
|
|
||||||||||||
|
|
|
|
|
|
|
= 9×6 |
|
|
|
|
|
|
|
|||||||
J x1y1 =0 |
|
|
|
|
|
Jy 2 |
|
|
= 40.5 см4 , Jx2 y 2 |
= 0 |
Jx3y3 =0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Практика №2. |
|
|
|
|
|
|
|
||||||
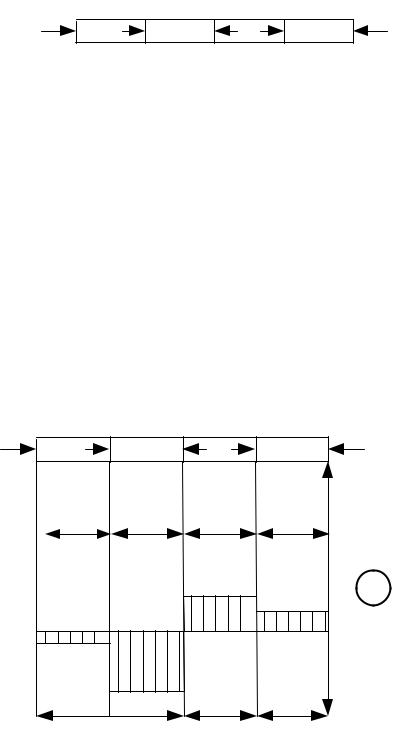
Задача 1. Построить эпюру продольных сил для стержня, изображенного на рис. 54.
Рис. 54
Решение
1. Опоры не показаны, поэтому определять неизвестные реакции не требуется.
Надо думать, что либо F1, либо F5, либо обе эти силы и являются реакциями, которые были найдены заранее.
Все силы, приложенные к телу, должны находиться в равновесии. В противном случае оно начинает движение с ускорением, что недопустимо для элемента строительной конструкции. Проверим равновесие сил в данном случае
∑z=F1+F2 –F3 +F4 –F5 = 10+30-70+50-20=90-90=0 .
Равновесие есть.
Рис.55 |
2. Нумеруем участки. На каждом из них произвольно показываем сечение.
Рассматривая либо левую, либо правую часть стержня, вычислим значение усилия
N, учитывая формулу:
1 участок (левая часть) |
N1 = -F1= - 10 кН |
(сжатие); |
||
2 |
участок (левая часть) |
N2 = - F1- F2= -10-30=-40 кН |
(сжатие); |
|
3 |
участок (правая часть) |
N3 |
= +F4– F5= 50-20=30 кН |
(растяжение); |
4 |
участок (правая часть) |
N4 |
= - F5= - 20 кН |
(сжатие). |
3. Строим график N(z), учитывая то, что на каждом из участков усилие N постоянно.
Убедимся для проверки, что высота и направление «скачков» на графике соответствует внешней нагрузке.
Из рис. 55, в частности, видно, что все участки стержня, за исключением участка №
3, сжаты, наиболее нагруженным является участок № 2 . Сжимающее усилие в нем равно
40 кН (около 4-х тонн).
Задача 2.2. Построить эпюру продольных сил для стержня, изображенного на рис. 56
при следующих значениях нагрузок:
F1= 40 кН, F2= 10кН, F3= 20 кН, q1= 30кН/м, q2 = 5кН/м .
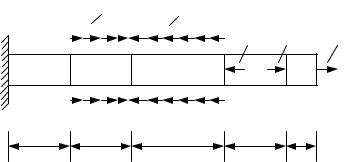
Рис. 56
Решение
1.Определим неизвестную опорную реакцию R, составив уравнение равновесия для всего стержня:
∑Z = 0, - R – F 1 + F2 + F3 + q1 ·2 - q2 ·3 = 0, R = - 40 + 10 + 20 + 30 · 2 – 5 · 3 = + 35 кН.

Рис. 57
2. Пронумеруем участки стержня (по направлению к заделке). В произвольном месте на каждом участке отметим поперечное сечение. Рассматривая либо левую, либо правую часть стержня (рис. 57), запишем выражение для продольной силы N на каждом участке.
На участках без распределенной нагрузки усилие N постоянно и не зависит от того,
в каком месте находится рассматриваемое сечение. На участках, где приложена распределенная нагрузка, от расположения сечения зависит, какая часть распределенной нагрузки придется на отсеченную часть стержня.
Другими словами, усилие N будет зависеть от расположения сечения (в данном случае линейно). Чтобы это учесть, расположение сечения будем отмечать переменным расстоянием, которое можно отсчитывать от края рассматриваемой части стержня (z3 ‒
для 3-го участка и z4 ‒ для 4-гоучастка).
При рассмотрении участков 1, 2, 3, 4 будем отбрасывать левую часть стержня. 1 участок. N1=F3= +20 кН (растяжение).
2 участок. N2 = F2+ F3 = 10 +20 =30 кН (растяжение).
3 участок. z3 изменяется от 0м до 3м (область определения N3) .
N3 = F3+ F2– F1- q2– z3 = 10 + 20 - 40 - 5z3= -10 - 5z3
Строим график функции N3 = -10 – 5 z3 (наклонная прямая).
График наклонной прямой обычно строят, подсчитав значения функции при
двух значениях аргумента, то есть, проводя ее через две точки. В данном случае
удобно определять ее значения на границах участка.
При z3 = 0м (правый край участка) N3 = -10-5· 0 = -10 кН; при z3 = 3 м (левый край участка) N3 = -10-5· 3 = -25 кН.
4 участок. 0м ≤ Z4 ≤ 2м (область определения N4)
N4 = F3+ F2– F1– q2· 3 + q1z4=20+10-40-5· 3 + 30- z4= -25 + 30 z4.
При z4 = 0 м N4 = - 25 + 30 · 0 = - 25 кН; при z4 =2 м N4 = - 25 + 30 · 2 = +35 кН.
При рассмотрении 5-го участка легче считать силы, приложенные к левой части стержня.
5 участок. N5 = + R= + 35 кН.
3. Откладываем вычисленные значения продольной силы от горизонтальной оси
(«+» ‒ вверх, «-» ‒ вниз).
На участках с распределенной нагрузкой подсчитанные значения соединяем наклонными линиями, а на остальных усилие N не зависит от zи изображается горизонтальными линиями. Расставляем знаки, делаем штриховку. Убеждаемся в том, что
«скачки» на графике по величине и направлению соответствуют внешним силам. Эпюра построена.
Когда стержень имеет опору только с одной стороны, усилия на участках можно определять, отбрасывая всегда ту часть стержня, к которой приложена неизвестная реакция. В этом случае неизвестная реакция никогда не потребуется для определения усилий, и эпюра может быть построена без определения реакций.
Например, в задаче 2.2 усилие на 5-м участке может быть получено
суммированием правых сил:
N5= F3 + F2– F 1 -q2· 3 + q1· 2 = 20 + 10-40 - 5 ·3 + 30·2 = 35кН.
Практика №3
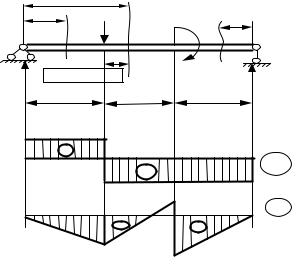
Задача 4.1. Построить эпюры усилий Qy и Мх для балки, изображенной на рис. 58,
аналитическим способом.
|
Рис. 58 |
Решение |
|
1. |
Определяем опорные реакции |
∑ |
0 ; p · 6 % % · 2 0 ; |
|
p · 6 % 18 % 12 · 2 0 ; |
p= rs t = 7 кН ; |
|
∑ |
p u0 ; % · 6 · 4 % 0 ; |
|
% · 6 12 · 4 % 18 0 ; |
p |
= trw r= 5 кН ; |
u |
|
Проверка: ∑ x p % 5 7 % 12 0 ; |
|
2. |
Нумеруем участки. На каждом участке выбираем произвольное сечение, |
показывая расстояние до него от левого или правого краев балки. |
|
3. |
На каждом участке записываем аналитические выражения для Qy и Мх, |
рассматривая равновесие правой или левой частей балки.
Полученные функции изображаем графически на эпюрах. |
|
1-й участок 0 ≤ z≤ 2 м |
|
5 кН; · 5 ; |
|
При = 0 |
Мх= 0 |
При = 2м |
Мх= 5 · 2 = 10 кНм ; |
2-й участок 2 ≤ }≤ 4 м
% 5 % 12 %7 кН;
· % · % 2 5 % 12 · % 2 %7 24; |
||||
При = 2м |
Мх= %7 · 2 24 |
10 кНм; |
||
При = 4м |
Мх= %7 · 2 24 |
%4 кНм; |
||
3-й участок 0 ≤ |
~≤ 2 м |
|
|
|
% p |
%7 кН ; |
p · Y %7 Y; |
||
При Y = 0 |
|
|
||
|
Мх= 0; |
|
||
При Y = 2м |
Мх= 7 · 2 14 кНм. |
|||
4. Эпюры Qy и Мх построены.
В рассмотренной задаче на балку воздействовали сосредоточенные нагрузки. В
следующей задаче демонстрируются основные приемы работы с равномерно-распреде-
ленными нагрузками.
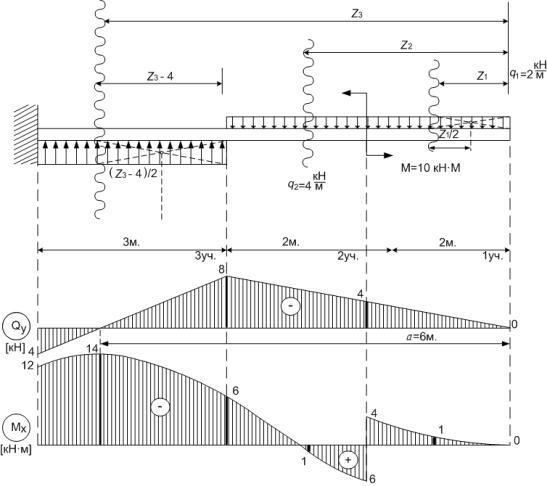
Задача 4.2. Построить эпюры поперечных сил и изгибающих моментов для балки,
изображенной на рис. 59.
Рис. 59
Решение
В данной балке можно построить эпюры, не определяя опорных реакций, если на всех участках выражения для Qy и Мх составлять, используя нагрузки, расположенные справа от сечения, а левую часть стержня (вместе с неизвестными реакциями)
отбрасывать.
Пронумеруем участки (по направлению). На каждом покажем произвольное
сечение, привязав его к правому краю балки.
Записываем аналитические выражения для Qy и Мх. Полученные функции
изображаем графически. |
|
|
1-й участок (0 ≤ z≤ 2 м) |
|
|
· 2 |
(наклонная прямая) |
|
• \€• 0; |
• \€ 2 · 2 4 кН; |
|
% ‚\·\] = % |
(квадратная парабола) |
|
• \€• 0; |
|
• \€ %4 кНм. |
Выпуклость параболы – вниз.
Касательная к ней горизонтальна в сечении, где Qy = 0, то есть на краю балки.
При вычислении значений усилий необходимо указывать сечения, для которых
производится подсчет. |
|
|
|
|
В задаче 4.1 указание выполнялось явно. |
|
|||
Например: |
при Y =2м |
Мх=… . |
|
|
В задаче 4.2 для этого используется значок • , который читается как «при». |
||||
Так, выражение • \€ можно прочитать как «значение Мх при 2 |
м». |
|||
Еще один способ заключается в том, чтобы обозначить все сечения балки |
||||
буквами: A, B, C, D, E и т.д. В этом случае можно, например, записать |
|
|||
ƒ |
, что будет обозначать: «значение в сечении D». |
|
||
Каждый вправе использовать тот способ указания сечений, который ему |
||||
нравится. |
2 м ≤ } ≤ 4 м |
|
|
|
2-й участок |
|
|
|
|
· 4 |
|
(наклонная прямая) |
|
|
• ]€• 4 |
кН; |
• ]€t 2 · 4 8 кН. |
|
|
Наклон графика Qy(z) одинаков на 1-м и 2-м участках. |
|
|||
% ‚\·]] = % 10 |
(квадратная парабола) |
|
||
• ]€ %4 10 6 кНм ; • ]€t %16 10 %6 кНм;
Более точно квадратная парабола строится по трем точкам.
Третью точку берем в середине участка.
• ]€Y %9 10 1 кНм
Выпуклость параболы - вниз. Экстремумов нет.
На стыке 1-го и 2-го участков приложен сосредоточенный момент 10 кНм. В
силу этого на эпюре Мх образовался скачок, по величине и направлению совпадающий с |
|
внешним моментом. |
|
3-й участок 4 м ≤ ~≤ 7 м |
|
Составляя выражения Qy(zY) и Мх ( Y) заметим, что теперь справа от сечения |
|
оказалась вся нагрузка q1 (равнодействующая q1 · 4м с плечом ( Y % 2) м) и часть нагрузки |
|
q2 (равнодействующая q2 ·( Y % 4) с плечом ( Y % 4)/2). |
|
· 4 % · Y % 4 2 · 4 % 4 · Y % 4 %4 Y 24 ; |
|
• k€t %16 24 8 кН ; |
• k€† %28 24 %4 кН. |
Наклонная прямая Qy( Y) имеет уклон в другую сторону и расположена круче, чем на 1-м и 2-м участках, поскольку тангенс угла ее наклона равен нагрузке q2, которая имеет другой знак и больше по величине, чем q1.
% 1 · 4 · Y % 2 % ‚]· kwt ]
=
10 % 2 · 4 · Y % 2 % t· kwt ] 2 % 24 Y 58
= Y ;
• k€t 2 · 4 % 24 · 4 58 %6 кНм ;• k€† 2 · 7 % 24 · 7 58 %12 кНм .
На стыке 2-го и 3-го участков к балке не приложены сосредоточенные силы и моменты. Поэтому в данном сечении эпюра Мх не имеет разрыва и излома, то есть гладкая. Квадратная парабола выпуклостью вверх и имеет экстремум в том сечении, где эпюра Qyпересекает ось (Qy= 0). Для построения параболы в данном случае следует третье значение считать не в середине участка (как на участке 2), а в месте экстремума.
Экстремальные значения усилий принято вычислять, поскольку часто они являются наибольшими и определяют положение опасного сечения.
Для того чтобы найти экстремум квадратной функции . 5 1 на некотором участке, следует сначала найти его расположение, то есть положение сечения, в котором Qy (z) обращается в нуль.

Пусть · 5, что следует из формулы). |
|
||
Пусть при z = функция Qy (z) обращается в нуль, то есть · 5 0, |
|||
откуда % p. |
|
|
|
Подставляем значение в выражение , получим экстремальное значение |
|||
момента. |
Y • k€> 0, то есть |
%4 24 0, откуда |
= 6 м. |
В данном случае |
|||
Экстремальное значение равно: |
|
|
|
• k€uм 2 · 6 % 24 · 6 58 %14 кНм. |
|
|
|
Проводим квадратную параболу через три точки.
Эпюры Qyи Мх построены.
Практика №4
Пример 1. Определить нормальное напряжение при изгибе балки (в МПа) в точке
А поперечного сечения, удаленной от нейтральной линии сечения на 15 см (рис. 60), если изгибающий момент M= 10 кНм = 1000 кНсм.
Рис. 60
Решение.
1. Определяем момент инерции сечения относительно оси z:
U #SY 18 · 36Y 69984 смt.12 12
2. Подставляем значения изгибающего момента, осевого момента инерции и координаты точки А в формулу для нормальных напряжений и находим напряжения:
σА = u‡‡rt••• 12 = 0,17 кН/см2 = 1,7 МПа
