
8658
.pdf
Лекция №8
Метод начальных параметров
Основные положения метода
Существует метод: метод начальных параметров, который позволяет свести решение к определению всего двух постоянных интегрирования. Для этого необходимо при решении использовать приём, который сводится к следующим правилам:
∙При решении задачи использовать единую (глобальную) систему координат для всех участков балки. Начало координат необходимо помещать на левом или правом конце балки.
∙Жесткость всех участков балки должна быть одинаковой и постоянной – EJx = const.
∙Прогиб и угол поворота в начале координат обозначим vo и θо, которые называются геометрическими или кинематическими начальными параметрами.
∙Изгибающий момент и поперечную силу в начале координат обозначим Mo и Qо,
которые называются статическими начальными параметрами.
∙При составлении выражения изгибающего момента для нагрузки от сосредоточенных моментов необходимо использовать следующую форму записи:
M = M(z-a)o.
∙Если распределённая нагрузка обрывается в сечении, расположенном левее сечения с абсциссой z(ось z направлена вправо), необходимо нагрузку продолжить до конца балки и одновременно приложить на этой части балки такую же нагрузку,
но противоположного направления (рис. 52).
Рис. 52 |
∙При интегрировании двучленов вида (z-a)kследует пользоваться следующей формулой:
∫(z −a)k |
dz = (z −a)k+1 . |
|
k +1 |
Произвольные постоянные интегрирования на всех участках получаются одинаковыми, и решение задачи сводится к нахождению лишь двух неизвестных при любом числе участков статически определимой балки.
Универсальное уравнение прогибов и углов поворота.
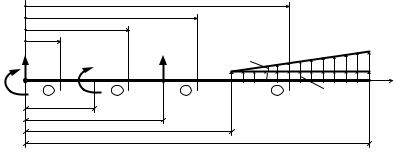
Рассмотрим балку постоянного сечения, нагруженную моментом M, cосредоточенной силой Fи распределёнными нагрузками (рис. 53). Ось z направим вправо. Направление нагрузок создают положительные изгибающие моменты.
Рассматриваемая балка имеет четыре участка, каждому из которых соответствует свое уравнение моментов, уравнение прогибов и углов поворота сечений.
Рис. 53 |
Для балки постоянного сечения дифференциальное уравнение записываем в виде
EJxv′′(z)= ±Mx (z).
Напоминаем, что в уравнении выбираем знак «плюс», если ось у направляем вверх,
и знак «минус», если ось у направляем вниз. Для каждого участка балки составляем дифференциальное уравнение изогнутой оси и дважды его интегрируем.
1-й участок. 0 ≤ z≤ а:
EJxv1′′ (z)= ±Mx(1) (z)= ±[Mo +Qo z].
EJ |
θ |
|
(z)= ± |
M z +Q |
z2 |
+ C |
. |
|
||||||||
1 |
|
|
|
|
|
|||||||||||
x |
|
|
|
o |
|
o |
2 |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
EJ v |
|
(z)= ± |
M |
z2 |
+Q |
|
z3 |
+C |
|
z + D . |
||||||
|
|
|
|
|
|
|
1 |
|||||||||
x |
1 |
|
|
o |
2 |
o |
6 |
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2-й участок. a ≤ z≤ b:
EJxv2′′(z)= ±Mx(2) (z)= ± Mo +Qo z + M(z −a)o .
EJ θ |
|
(z)= ± |
M z +Q |
z2 |
+M(z −a) |
+C |
. |
|||||||
2 |
|
|
||||||||||||
x |
|
|
o |
|
o |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(z)= ± |
|
|
z2 |
|
|
z3 |
(z −a)2 |
|
|
|||
EJxv2 |
Mo |
|
+Qo |
|
|
+ M |
|
|
+C2 z +D2 |
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3-й участок. b ≤ z≤ c:
EJxv3′′ (z) = ± Mx(3) (z) = ± Mo +Qo z + M (z − a)o + F (z − b) .
|
|
|
|
z2 |
|
(z − b)2 |
|
|
|||
EJxθ3 |
(z) = ± Mo |
z +Qo |
|
|
+ M(z − a) + F |
|
+ C3 . |
||||
|
|
||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
z3 |
(z − a)2 |
(z − b)3 |
|
||||
EJxv3 |
(z) = ± Mo |
|
+ Qo |
|
|
+ M |
+ F |
|
|
+ C3 z + D3 . |
|
|
|
|
|
||||||||
|
|
2 |
|
|
6 |
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4-й участок. c ≤ z≤ l:
EJx v4′′ (z) = ± Mx( |
4 |
|
|
|
|
|
+ Qo z + M |
(z − a) |
o |
+ F (z − b) + q |
(z − c)2 |
+ tgα |
(z − c)3 |
|
||||||||
|
) (z) = ± Mo |
|
2 |
|
|
|
6 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
(z − b)2 |
(z − c)3 |
|
(z − c)4 |
|
|
|
|||||||
|
|
|
|
|
z2 |
|
|
|
|
|
||||||||||||
EJxθ4 |
(z) = ± Mo |
z + Qo |
|
|
|
+ M (z − a) + F |
|
+ q |
+ tgα |
|
|
|
+ C4 . |
|
||||||||
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
6 |
|
|
24 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
z3 |
(z − a)2 |
(z − b)3 |
(z − c)4 |
|
(z − c)5 |
|
|
|||||||||
EJx v4 |
(z) = ± Mo |
|
+ Qo |
|
|
|
+ M |
+ F |
|
|
+ q |
+ tgα |
|
|
|
+ C4 z + D4 . |
||||||
2 |
6 |
|
6 |
120 |
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
24 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изогнутая ось балки есть плавная кривая. На границах участков балки значения углов поворота и прогибов, вычисленных из уравнений соседних участков, будут равны.
Эти равенства называются условиями плавности и непрерывности изогнутой оси на
границе участков.
Рассмотрим эти условия, используя полученные для балки выражения.
Граница 1-го и 2-го участков. z= a: θ1(a) = θ2(a). |
Отсюда следует С1 |
= С2. |
|
v1(a) = v2(a). |
Отсюда следует D1 = D2. |
|
|
Граница 2-го и 3-го участков. z= b: θ2(b) = θ3(b). |
Отсюда следует С2 |
= С3. |
|
v2(b) = v2(b). |
Отсюда следует D2 = D3. |
|
|
Граница 3-го и 4-го участков. z= c: θ3(c) = θ4(c). |
Отсюда следует С3 = С4. |
||
v3(c) = v4(c). |
Отсюда следует D3 = D4. |
|
|
Из полученного решения следует, что, используя при решении правила, изложенные
в пункте 2.1, постоянные интегрирования всех участков балки всегда будут равны и могут быть заменены фактически двумя постоянными интегрирования независимо от количества участков балки:
С1 = С2 = С3 = С4 = ….. = С. D1 = D2 = D3 = D4 = ….. = D.
С учётом введённых обозначений угла поворота и прогиба в начале координат из
равенств (2.3) при z= 0 получим следующие выражения постоянных интегрирования С и
D:
C = EJxθo, D = EJxvo,
т.е. постоянная интегрирования С есть угол поворота в начале координат, а D – прогиб в начале координат, умноженные на жёсткость балки при изгибе.
Из формул следует, что выражения моментов, углов поворота и прогибов предыдущих участков входят как составная часть выражений для последнего (4-го )

участка балки. Это позволяет результаты решения для всех участков объединить и записать формулы для углов поворота и прогибов в виде единого выражения для всех участков, используя следующий приём:
|
k |
|
0 |
при z £a |
|
|
|
z³a (z - a) |
|
|
|
||||
|
= |
|
|
|
|
. |
|
|
(z - a) |
k |
при z |
|
|||
|
|
|
|
³a |
|||
|
|
|
|
|
|
|
|
Применяя правило, из формулы для погибов 4-го участка при z<a получим выражение прогиба 1-го участка, при z<b получим выражение прогиба 2-го участка, при z<cполучим выражение прогиба 3-го участка.
Таким образом, для уравнения прогибов балки с учётом можно записать обобщённое уравнение прогибов в виде:
EJxv(z) = EJxvo |
|
z2 |
|
z3 |
(z−a)2 |
(z−b)3 |
(z−c)4 |
|
(z−c)5 |
|
||
+ EJxθoz ± Mo |
|
+Qo |
|
+M |
+F |
|
+q |
+tgα |
|
|
||
2 |
6 |
6 |
120 |
|||||||||
|
|
|
|
2 |
24 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение является универсальным уравнениемпрогибов балки, поскольку может быть использовано для определения прогибов для балки с любым числом участков.
Определение прогибов балок с помощью универсального уравнения требует выполнения следующих правил.
1.Уравнение применимо для решения балок только с постоянной жёсткостью EJx = const.
2.Начало координат необходимо помещать либо на левом конце балки, либо на правом конце балки.
3.Знак «плюс» перед квадратными скобками следует выбирать, если ось у направить вверх, а знак «минус», если ось у направить вниз.
4.Прогиб балки всегда выражается через четыре начальных параметра: два статических
Мо, Qo и два геометрических vo, θo, поэтому метод называется методом начальных параметров.
5.Неизвестный прогиб vo и угол поворота θo в начале координат необходимо определять из условий закрепления балки .В частности:
∙ |
если в начале координат расположена жёсткая заделка, то |
vo = 0 |
и |
θo = 0; |
∙ |
если в начале координат расположена шарнирная опора, то |
vo = 0 |
и |
θo ≠ 0; |
∙ |
если в начале координат отсутствует опора (свободный край), то |
vo ≠ 0 и θo ≠ 0. |
||
6.При использовании универсального уравнения условия плавности и непрерывности на границах участков балки выполняются автоматически.
7.Знак слагаемых, стоящих в квадратных скобках, определяют по правилу знаков для изгибающих моментов. В частности:
∙если силы F и нагрузки q направлены вверх, то изгибающие моменты от такой нагрузки будут положительными независимо от выбора положения начала координат;
∙если силы F и нагрузки q направлены вниз, то изгибающие моменты от такой нагрузки будут всегда отрицательными;
∙изгибающие моменты от моментной нагрузки будут положительными, если сосредоточенные моменты Мдействуют по часовой стрелке при размещении начала координат на левом конце балки;
∙при размещении начала координат на правом конце балки сосредоточенный момент М необходимо вводить в уравнение со знаком «плюс», если он действует против часовой стрелки.
8.Универсальное уравнение углов поворота сечений балки получается из уравнения путём его дифференцирования: EJxθ(z) = EJxv′ (z).

ПРАКТИКА

Практика №1.
Пример 1. Для заданного поперечного сечения стального стержня, состоящего из следующих элементов:
1.вертикального листа 400 х 12 мм;
2.прокатного двутавра №20;
3.прокатного швеллера №20;
4.неравнополочного уголка 100 х 65 х 10 мм,
необходимо определить:
-положение центра тяжести поперечного сечения (т. С);
-главные центральные оси поперечного сечения;
-главные центральные моменты инерции поперечного сечения;
-главные центральные радиусы инерции сечения.
Ре ш е н и е.
Геометрические характеристики элементов, составляющих заданное сечение:
№ |
|
Площадь в |
Моменты инерции сечения элементов в см4 |
|||||
эл- |
|
см2 |
|
|
|
|
|
|
Элементы |
|
Jx i |
|
Jy i |
J x i y i |
|||
та |
|
Аi |
|
|
|
|
|
|
1 |
Вертикальный лист |
А1 = 48.0 |
Jx 1 |
= 6400 |
Jy 1 |
=5.76 |
Jx 1 y 1 |
= 0 |
|
400х12 |
|
|
|
|
|
|
|
2 |
Двутавр №20 |
А2= 26.8 |
Jx 2 |
= 115 |
Jy 2 |
= 1840 |
J x 2 y 2 |
= 0 |
3 |
Швеллер №20 |
А3= 23.4 |
Jx 3 |
= 1520 |
Jy 3 |
= 113 |
J x 3 y 3 |
= 0 |
4 |
Уголок 100х65х10 |
А4= 15.67 |
J x 4 |
= 51.68 |
Jy 4 |
= 155.52 |
J x 4 y 4 |
= 51.18 |
1). Общая площадь составного сечения
А = ∑ Аi= 48.0 + 26.8 + 23.4 + 15.67 = 113.87 см2.
2). Статические моменты заданного сечения относительно осей х1 и у1 |
|
|||||||||||
Sx 1 |
=∑Ai yi |
= 48 · 0 + 26.8 · 15 + 23.4 · (-10) + 15.67 · (-18.36) = - 119.7 см3, |
||||||||||
Sy 1 |
=∑Ai xi |
= 48 · 0 + 26.8 · 10.6 + 23.4 · 2.67 |
+ 15.67 · (-3.97) = 284.35 см3. |
|||||||||
3). Координаты центра тяжести составного сечения |
|
|
|
|
|
|||||||
|
|
Sy 1 |
|
284.35 |
|
Sx 1 |
−119.7 |
|
|
|||
|
xc = |
|
|
= |
|
=2.50см, yc = |
|
|
= |
|
=−1.05 |
см. |
|
|
A |
113.87 |
A |
|
113.87 |
||||||
|
|
|
|
|
|
|
|
|
||||
4). Координаты центров тяжести элементов сечения относительно осей х и у

точка С1: a1 = 1.05 см, |
|
|
|
b1 = - 2.5 см; |
|
|||||||||||||
точка С2: а2 = 15 + 1.05 = 16.05 см, |
b2= 10.6 – 2.5 = 8.1 см; |
|
||||||||||||||||
точка С3: а3 = - (10.0 – 1.05) = - 8.95 |
см, |
b3= 2.67 – 2.50 = 0.17 см; |
|
|||||||||||||||
точка С4: а4 = - (18.36 – 1.05) = - 17.31 см, |
b4 = - (3.97 + 2.5) = - 6.47 см. |
|||||||||||||||||
5). Моменты инерции сечения относительно осей х и у |
|
|||||||||||||||||
Jx |
= ∑( Jx i + Ai ai2 ) = [6400 + 48 · 1.052] + [115 + 26.8 ·16.052] + |
|
||||||||||||||||
|
|
+ [1520 + 23.4 · (-8.95)2] + [51.68 + 15.67 · (-17.31)2] = 21613.04 см4, |
||||||||||||||||
Jy |
= ∑( Jy i + Ai bi2 ) = [5.76 + 48 · (-2.5)2] + [1840 + 26.8 · 8.12] + |
|
||||||||||||||||
|
|
+ [113 + 23.4 · 0.172] + [155.52 + 15.67 · (-6.47)2] = 4829.27 см4, |
|
|||||||||||||||
Jxy |
= ∑( Jx i y i + Ai ai |
bi ) = [0 + 48 · 1.05 · (-2.5)] |
+ [0 + 26.8 ·16.05 · 8.1] |
+ |
||||||||||||||
|
|
+ [0 + 23.4 · (-8.95) · 0.17] + [51.18 + 15.67 · (-17.31) · (-6.47)] = 5128.68 см4. |
||||||||||||||||
6). Главные центральные моменты инерции заданного сечения |
|
|||||||||||||||||
|
|
|
|
|
J max |
= J1,2 = |
Jx +Jy |
± |
1 |
|
[(Jx - Jy )2 + 4 J 2xy ]= |
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
min |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
21613.04 + 4829.27 |
± |
1 |
|
[(21613.04 - 4829.27)2 + 4×5128.68 2 ] |
= 13221.16 ± 9834.99. |
||||||||||||
|
|
|
||||||||||||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Jmax |
= J1 = 23056.15 см4, |
|
|
|
|
Jmin = J2 = 3386.17 |
см4. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка: Jx + Jy = 21613.04 + 4829.27 = 26442.31 см4,
J1 + J2= 23056.15 + 3386.17 = 26442.32 см4.
7). Углы наклона главных центральных осей инерции сечения |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
tgαmax |
= |
|
Jxy |
|
|
= |
|
|
|
5128.68 |
|
= - 0.28138, |
|
|
αmax |
= -15.72 |
o |
. |
|||||||||||||||||||
Jy |
|
|
|
|
4829.27 - 23056.15 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
- Jmax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
tgαmin |
= |
|
|
Jxy |
|
|
= |
|
|
|
|
|
5128.68 |
|
|
= 3.5539325, |
|
|
|
αmax |
= 74.28 |
o |
. |
||||||||||||||
Jy |
|
|
|
|
|
4829.27 - 3386.17 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
- Jmin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Проверка: |
|
αmax |
|
+ |
|
αmin |
|
= 15.72o + 74.28o = 90o. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
8). Главные центральные радиусы инерции |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
imax = |
|
Jmax |
|
|
= |
|
|
|
23056.15 |
|
= 14.23 см, imin = |
Jmin |
= |
|
3386.17 |
|
= 5.45 см. |
||||||||||||||||||||
|
A |
113.87 |
|
113.87 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|||||||||||||||||
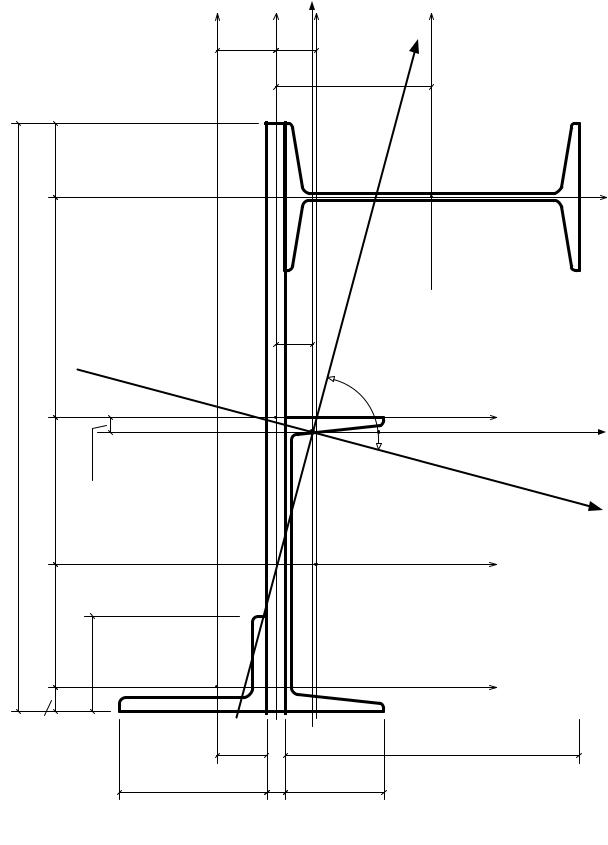
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
у4 |
|
у1 |
у3 |
|
|
|
|
у2 |
|
|
|
|
3.97 см |
|
2.67 см |
min (2) |
|
|
|
|
|
|||
|
|
|
|
|
10.60 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х2 |
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
2.50 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
.2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
= |
7 |
|
|
|
|
|
|
|
|
|
|
|
IN |
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
c |
1 |
|
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
MAX = - |
15. |
72 |
O |
х |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max (1) |
|
|
|
|
|
|
|
|
|
|
|
|
х3 |
|
|
|
|
c3 |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
х4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3.37 см |
|
|
|
|
|
|
20.00 см |
|
|||
10.00 см |
1.20 см |
7.60 см |
|
|
|
|
|
|
|
|||

Пример 2. Для заданного поперечного сечения стержня, состоящего из следующих фигур:
1.полукруга с диаметром 8 см;
2.равнобедренного треугольника 6х9 см;
3.прямоугольного отверстия 2х3 см;
необходимо определить:
-положение центра тяжести поперечного сечения (т. С);
-главные центральные оси поперечного сечения;
-главные центральные моменты инерции поперечного сечения;
-моменты сопротивления сечения.
Ре ш е н и е.
Вычисление геометрических характеристик фигур, составляющих заданное сечение,
выполнено и представлено в таблице.
1). Определяем общую площадь заданного сечения
А = А1 + А2 – А3 = 25.13 + 27 - 6 = 46.13 см2. 2). Определяем статический момент сечения относительно оси х1.
Sx 1 = y1 A1 + y2 A2 - y3 A 3 = 0 + (-4.7) ×27 - (-3.2) ×6 = -107.7 см3 .
3). Определяем координаты центра тяжести заданного сечения.
Поскольку заданное сечение имеет ось симметрии (ось у), то центр тяжести располагается на этой оси, поэтому необходимо определить только координату ус
yc = Sx 1 = - 107.7 = - 2.335 см .
A 46.13
4). Через полученный центр тяжести проводим горизонтальную ось х.
Оси х, у является искомыми главными центральными осями инерции заданного сечения,
т.к. ось у – |
ось симметрии и Jxy = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5). Вычисляем главные центральные моменты инерции сечения |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Jx |
= (Jx 1 + a12 A1 )+ (Jx 2 + a22 A 2 )- (Jx 3 + a32 A 3 )= [0.28 ×100.53 + 2.335 2 ×25.13 ]+ |
|||||||||||||||||||||||||||||||
+ |
[121.5 + (- 2.365) 2 ×27] - [4.5 + (- 0.865) 2 ×6]= 428.69 см4 , |
|
|
|
|
|
|
|
||||||||||||||||||||||||
Jy |
= Jy |
+ |
Jy |
2 |
- Jy |
= 100.53 + 40.5 - 2 = 139.03 см4 , |
Jxy = Jx y |
1 |
+ Jx |
y |
2 |
- Jx |
y |
= 0 . |
||||||||||||||||||
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
|
3 |
||||
Из полученного решения следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Jmax = J1 = Jx = 428.69 см4, Jmin = J2 = Jy = 139.03 см4 . |
|
|
|
|
|
|||||||||||||||||||||
6). Вычисляем осевые моменты сопротивления сечения |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
Wx( 1) = |
Jx |
= |
428.69 |
= 92.49см3 , |
Wx( 2 ) = |
|
|
Jx |
|
|
= |
428.69 |
= 51.25см3 , |
|
|
|||||||||||||||
|
|
y1 |
4.635 |
|
|
y2 |
|
|
8.365 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
W |
|
= |
|
Jу |
|
= |
139.05 |
= 34.76см3 . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
у |
|
х |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
