
8658
.pdf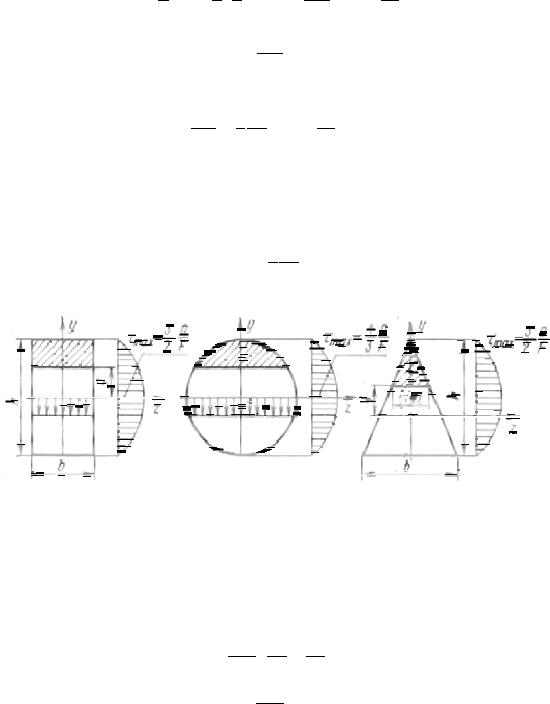
Таким образом, в т очке А поперечного сечения балки действ ует нормальное напряжение σA=1,7 МПа.
Пример 2.
В качестве примера применения формулы Журавского пост роим эпюру касательных напряжений для случая прямоугольного поперечного сечения балки.
Учитывая, что для этого сечения
получаем
где F=bh- площадь прямоугольника.
Как видно из форм улы, касательные напряжения по высоте сечения меняются по закону квадратической п араболы, достигая максимума на нейтральной оси
Рис. 61
В круглом сечен ии (рис. 61) эпюра касательных напряже ний ограничена кривой,
имеющей максимум на нейтральной оси. Учитывая, что статический момент полукруга и момент инерции круга
получаем

m=> 163 · ˆ) 43 ·
Следовательно, максимальные касательные напряжения в круглом сечении на 33%
больше средних напряжений m / , по которым, например, обычно проводится расчет заклепок.
Для треугольного сечения с основанием b и высотой h (рис. 61), имеем nŠ=e # 36 · ‹2S3 % 6Œ · ‹S3 6Œ ;
: #S36Y,
m 12#SY · ‹2S3 % 6Œ · ‹S3 6Œ ; m=> 32 ·
Максимальное напряжение имеет место на расстоянии y=h/6 от нейтральной линии, то есть в точках средней линии треугольника.
При изгибе тонкостенных профилей касательные напряжения определяются по
следующей формуле:
m · nŠ=e, : · •
где δ - толщина стенки тонкостенного профиля.
Необходимо отметить также, что формулой Журавского можно пользоваться только в случае прямого изгиба.
Определить касательные напряжения в указанных точках двутаврового сечения и построить эпюру касательных напряжений при величине поперечной силы Q=50 кН
(рис.62).
Рис. 62

Решение.
Характерной особенностью этого сечения является резкое изменение ширины сечения при переходе от стенки двутавра к его полке. В основном поперечную силу воспринимает стенка, а на долю полок приходится небольшая ее величина.
Покажем, как определяется статический момент площади для любой произвольной точки сечения двутавра. Для этого рассмотрим произвольную точку К. Проведем через эту точку линию, параллельную оси Oz. Статический момент площади верхней отсеченной части (заштрихованой на рис. 63) может быть найден как сумма статических
моментов двух площадей A1 и A2
nотс . 6 . 6 .
Рис. 63
Наибольшей величины статический момент площади отсеченной части относительно нейтральной линии сечения Oz достигает для половины сечения.
Следовательно, максимальные касательные напряжения возникают в волокнах нейтрального слоя.
Точка №1 сечения принадлежит наиболее отдаленному волокну. Точки №2 и №3
лежат в месте перехода от полки к стенке: точка №2 принадлежит полке, точка №3 –
стенке сечения. Точка №4 лежит в центре тяжести сечения и принадлежит нейтральной линии сечения. Сечение симметрично расположено по отношению к оси Oz. Поэтому напряжение в точке №5 будет таким же, как в точке №3, напряжение в точке №6 – таким же, что и в точке №2, напряжение в точке №7 – таким же, что и в точке №1.
Вначале найдем момент инерции сечения относительно оси Oz:
U 2 Ž1012· 23 112 · 2 · 10• 1,212· 203 5653,33 см4.
Касательное напряжение в точке №1 поперечного сечения равно нулю, так как отсеченная часть сечения в данном случае представляет собой пространство над сечением,
и ввиду отсутствия отсеченной площади, статический момент этой площади равен нулю.
С другой стороны, если в качестве отсеченной площади рассматривать все сечение, то статический момент всей площади относительно нейтральной линии сечения z , как центральной оси, равен нулю.
Для определения касательного напряжения в точке №2 проводим через точку №2
линию, параллельную оси Oz. Отсеченная площадь лежит выше этой линии и составляет
.отс2 =2·10=20см2. Вычисляем расстояние от центра тяжести отсеченной площади до оси Oz.
Оно равно 11см. Находим касательные напряжения в точке №2:
m2 |
· n 2 |
|
50 · 103 · 10 · 2 · 11 · 10%6 |
10 |
%6 |
1,95 МПа. |
#U |
10 · 10%2 · 5653,33 · 10%8 |
|
При определении касательного напряжения в точке №3 следует помнить, что статический момент площади отсеченной части в этом случае остается прежним, так как точки №2 и №3 находятся на одинаковом расстоянии от оси Oz. Только точка №2
принадлежит полке, а точка №3 принадлежит стенке двутавра. В связи с этим касательное напряжение в точке №3 будет равно:
m3 |
· n 3 |
50 · 103 · 10 · 2 · 11 · 10%6 |
10 |
%6 |
16,21 МПа. |
)U |
1,2 · 10%2 · 5653,33 · 10%8 |
|
Для определения напряжения в точке №4, проведем через эту точку линию,
совпадающую с осью Oz. Отсеченная площадь представляет собой тавр. Статический момент площади тавра вычислим, используя выражение (а), приведенное выше. В нем A1
представляет собой площадь полки, A2− площадь половины стенки; y1− расстояние от центра тяжести полки до оси Oz; y2− расстояние от центра тяжести половины площади стенки до оси Oz. Касательные напряжения в точке №4 будут равны:
m4 |
· n 4 |
|
50 · 103 · 10 · 2 · 11 1,2 · 10 · 5 · 10%6 |
10 |
%6 |
20,64 МПа. |
)U |
1,2 · 10%2 · 5653,33 · 10%8 |
|
Как уже отмечалось выше, в силу симметрии τ5=τ3=16,21 МПа, τ6=τ2=1,95 МПа;
τ7=τ1=0.
Откладываем найденные значения касательных напряжений от базисной линии и строим эпюру касательных напряжений (рис. 63).
Практика №5
Пример 1.. Подобрать сечение стальной балки из прокатного двутавра.
Расчётные характеристики балки: [ σ ] = 160 МПа, [ τ ] = 100 МПа, Е = 2٠105МПа.
Длина пролёта балки l= 6 м. Допускаемый прогиб [ f ] = l/ 400 = 6000 мм/ 400 = 15 мм.
1. Определяем размеры прокатного двутавра из условия прочности балки на изгиб.
Wx ³ |
M |
= |
8000 кНсм |
= 500 см3 . |
|
x |
|
|
|||
σ |
16 кН / см3 |
||||
|
[ ] |
|
|
|
|
Из таблицы 1. Сталь горячекатанная. Балки двутавровые (ГОСТ 8239-72*) находим следующий номер профиля:
Двутавр №30а: Wx = 518 см3, Jx = 7780 см4, S*x = 292 см3, d = 0,65 см.
2. Выполняем проверку балки на срез.
τ = |
|
Q S*x |
£ |
[τ ], |
|
|
|
|
y |
|
|
||||
|
|
|
|
|
|
||
|
|
J x d |
|
|
|
|
|
τ = |
|
40 кН ×292см3 |
= 2,3кН / см2 = |
||||
7780см4 ×0,65 |
см |
||||||
|
|
||||||
=23 МПа << [τ ] = 100 МПа.
3.Определяем жёсткость балки при изгибе.
EJx = 2٠104кН/см2× 7780 см4 = 15560 ٠104кНсм2 = 15560 кНм2.
4. Балка имеет 2 участка.
Составляем дифференциальное уравнение для каждого участка и дважды интегрируем.
Начало координат помещаем на левом конце балки. Ось у направляем вниз.
I участок. 0<z<4 м |
II участок. 4 м<z< 6 м |
|
|
EJxv1// = - Мх = - (20 z) |
EJxv2// = - Мх = - (20 z – 60 (z-4)) |
EJxθ1 = - 10 z2 + C1 |
EJxθ2 = - 10 z2 + 30 (z-4)2 + C2 |
|
|
EJx v1 = - (10/3) z3 + C1 z + D1 |
EJx v2 = - (10/3) z3 + 10 (z-4)3 + C2 z + D2 |
|
|
5. Определяем постоянные интегрирования.
·Условие плавности изогнутой оси при z = 4 м: θ1(4) = θ2(4). Отсюда находим С1 =
С2.
· Условие непрерывности изогнутой оси z = 4 м: v1(4) = v2(4). Отсюда находим D1 =
D2.
· Условие закрепления балки при z = 0: v1(0) = vA= 0. Отсюданаходим D1 = D2 = 0.
∙Условие закрепления балки при z = 6 м: v2(6) = vВ= 0. Отсюданаходим С1 = С2 = 320/3.
С учётом полученных значений постоянных интегрирования для углов поворота и
прогибов сечений балки окончательно получаем следующие выражения:
I участок. 0<z<4 м |
II участок. 4 м<z< 6 м |
|
|
EJxθ1 = - 10 z2 + 320/3 |
EJxθ2 = - 10 z2 + 30 (z-4)2 + 320/3 |
|
|
EJx v1 = - (10/3) z3 + (320/3)z |
EJx v2 = - (10/3) z3 + 10 (z-4)3 + (320/3)z |
|
|
Эпюры углов поворота и прогибов балки показаны на рис. 64.
Максимальный прогиб в сечении балки 1 участка, где θ1 = 0:- 10 z2 + 320/3 = 0.
Отсюда находим координату сечения z ≈ 3,266 м.
Максимальный прогиб в этом сечении будет равен f≈ 14,93 мм.
Прогиб в середине пролёта балки при z = 3 м равен vсер. ≈ 14,78 мм.
Максимальный прогиб и прогиб в середине пролёта отличаются всего лишь на 1%, поэтому при проверке балок на жёсткость достаточно определить прогиб в середине пролёта.

Рис. 64
Пример 2. Выполнить расчёт деревянных балок с прямоугольным и круглым сечением.
Расчётные характеристики балок: [ σ ] = 12 МПа, [ τ] = 2 МПа, Е = 104МПа, [ f ] = l/200. 1.Определяем размеры поперечного сечения балок.
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
Балка с прямоугольным поперечным сечением. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mx |
b×4b2 |
|
6125кНсм |
|
|
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
h=2b |
|
|
|
|
|
|
x Wx ³ |
[σ ] |
; Wх = |
|
|
³ |
|
|
= 5104,2см |
|
. b = 19, 7 см ≈ 20 |
см. h = 40 см. |
||||||||||
|
|
|
|
|
|
6 |
|
1,2кН /см2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1,3МПа < [τ ]=2МПа. |
|
|||||||||
|
|
|
|
|
|
|
|
3 Qу |
70кН |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
τ = |
|
|
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
= 1,5× |
|
= 0,13кН /см |
|
|
||||||||||||
2 |
А |
(20×40)см2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Jx= |
bh3 |
= |
20×403 |
|
= 106667см4 . EJx = 103кН/см2 · 106667 см4 |
|
= 10666,7 кНм2. |
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
12 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

Балка с круглым поперечным сечением.
W ³ |
Mx |
; |
W = π ×d |
3 |
³ |
6125кНсм |
= 5104,2см3 . d= 37,3 см ≈ 40 см. |
|
[σ ] |
|
1,2кН / см2 |
||||||
x |
|
х |
32 |
|
|
|
||
d |
|
4 Q |
|
|
|
|
|
|
|
|
|
|
|
τ = |
у |
= |
4 |
× |
|
70 |
кН |
2 = 0,074кН /см2 = 0,74МПа < [τ]=2МПа. |
|||
x |
|
3 |
(π ×20 |
2 |
)см |
|||||||
|
|
3 А |
|
|
|
|
|
|||||
y |
Jx= π d4 |
= π ×404 |
= 125664см4 . EJx = 103кН/см2 · 125664 см4 |
= 12566,4 кНм2. |
||||||||
|
|
64 |
|
|
64 |
|
|
|
|
|
||
2. Определяем перемещения балки. Начало координат помещаем на границе участков
(рис. 65). Ось у направляем вниз.
1 участок. 0 <z< 4 м |
|
2 участок. 0 <z< 2 м |
|
|
||
|
|
|
|
|
|
|
Q1x = 70 – 40 z |
Q2x = 70 – 40 ·4 + 120 = 30кН |
|
|
|||
M1х = 70z – 20 z2 |
M2х = -20+ 70(4+z)- 40·4(2+z)+ 120z = -60 + 30z |
|||||
EJxv1// = - М1х = - 70z+ 20z2 |
EJxv2// =- М2х = 60 – 30 z |
|
|
|
||
EJxθ1 = - 35z2 + 20/3 z3 + C1 |
EJxθ2= 60z – 15 z2 + C2 |
|
|
|
||
EJxv1 = - 35/3 z3 + 5/3 z4 + C1z + D1 |
EJxv2 = 30z2 – 5 z3 + C2z + D2 |
|
|
|||
3. Постоянные интегрирования определяем из следующих условий: |
|
|
||||
|
|
|
|
|
|
|
Условие закрепления на опоре А: |
|
z1 |
= 0 |
v1(0) |
= 0 |
|
Условие плавности на границе участков: |
z1 |
= 4 м, z2 = 0 |
θ1(4) = θ2 (0) |
|
||
Условие непрерывности на границе |
|
z1 |
= 4 м, z2 = 0 |
v1(4) |
= v2(0) |
|
участков: |
|
|
|
|
|
|
Условие закрепления на опоре В: |
|
z2 |
= 0 |
v2(0) |
= 0 |
|
В результате получим следующие значения для постоянных интегрирования:
D1 = 0, D2 = 0, C1 = 80, C2 = - 53,33.
4. Вычисляем перемещения в сечениях балок и строим эпюры перемещений.
z1(м) |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
z2(м) |
|
|
|
|
0 |
1 |
2 |
|
|
|
|
|
|
|
|
EJxθ |
80,00 |
51,67 |
- 6,67 |
-55,00 |
-53,33 |
-8,33 |
6,67 |
|
|
|
|
|
|
|
|
EJxv |
0,00 |
70,00 |
93,33 |
60,00 |
0,00 |
- 28,33 |
- 26,66 |
|
|
|
Прямоугольная балка |
|
|
|
|
|
|
|
|
|
|
|
|
θ (рад) |
0,00750 |
0,00484 |
- 0,00063 |
- 0,00516 |
- 0,00500 |
- 0,00078 |
0,00063 |
|
|
|
|
|
|
|
|
v (мм) |
0,00 |
6,56 |
8,75 |
5,63 |
0,00 |
- 2,66 |
- 2,50 |
|
|
|
|
|
|
|
|
|
|
|
Круглая балка |
|
|
|
|
|
|
|
|
|
|
|
|
θ (рад) |
0,00637 |
0,00411 |
- 0,00053 |
- 0,00438 |
- 0,00424 |
- 0,00066 |
0,00053 |
|
|
|
|
|
|
|
|
v (мм) |
0,00 |
5,57 |
7,43 |
4,78 |
0,00 |
- 2,25 |
- 2,12 |
|
|
|
|
|
|
|
|

Рис. 65 |
5. Проверяем условие жёсткости балок:
Прямоугольная балка - v = 8,75 мм < [ f ] = 4000 мм / 200 = 20 мм.
Круглая балка - v= 7,43 мм < [ f] = 4000 мм / 200 = 20 мм.
Таким образом, полученные из условий прочности размеры поперечного сечения балок обеспечивают также выполнение условий жёсткости балок
На рис. 66 приведены задачи для самостоятельного решения методом непосредственного интегрирования по участкам. Подобрать сечение стальной балки из прокатного двутавра.
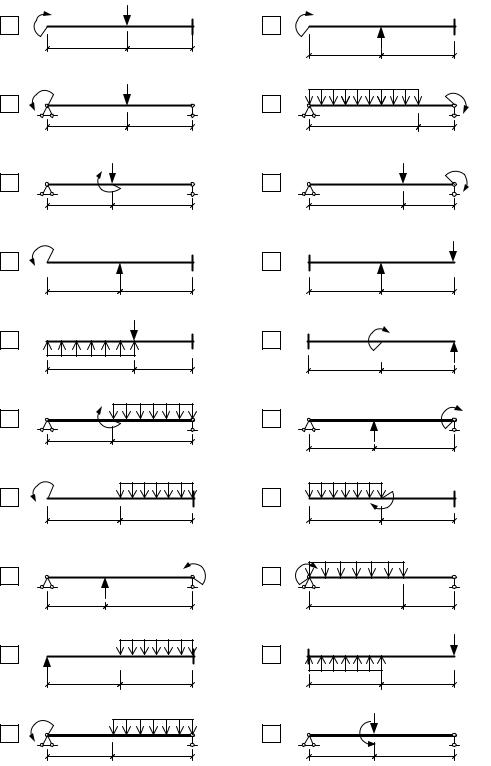
Расчётные характеристики балок: [ σ ] = 160 МПа, [ τ ] = 100 МПа, Е = 2٠105МПа.
Допускаемый прогиб [ f ] = l/ 100, где l– длина балки.
Рис. 66
