7591

60

Восстанавливая перпендикуляры к направлению скоростей вектора '! и '!…, получаем МЦС звена 4 (точку P4). Поскольку треугольник

ADP4 равнобедренный, то AP4 = DP4. Отсюда следует, что скорости точек A и D по модулю равны: '… ' 100 смс .

Движение колеса 5 плоскопараллельное. Мгновенный центр

61

Глава 3. ДИНАМИКА

Введение

Динамика – это раздел теоретической механики, в котором изучается механическое движение материальных тел с учетом действующих на них сил.

Среди практических задач механики лишь небольшое число допускает чисто статическое или чисто кинематическое исследование; в большинстве случаев необходимо полное, т.е. динамическое изучение механических явлений. При этом используются установленные в статике способы приведения сил, а также разработанные в кинематике методы описания и изучения движения. Поэтому динамика представляет собой наиболее общий раздел механики, имеющий особое значение для решения многих практических задач в различных областях техники.

Воснову динамики положены некоторые исходные положения, аксиомы, достоверность которых проверена многовековой практической деятельностью людей.

Эти аксиомы были впервые сформулированы Галилеем (1564-1642г.),

ав современном виде Ньютоном (1643-1727г.) и получили название основных законов динамики. Законы динамики Галилея-Ньютона были сформулированы для простейшего материального образа – материальной точки. Материальная точка – это тело конечной массы, размеры которого так малы, что различием в движении его частиц можно пренебречь.

Воснове классической динамики лежат два допущения, утверждающих существование абсолютного пространства и абсолютного времени.

Предполагается, что пространство обладает чисто геометрическими свойствами, не зависящими от помещенных в него материальных объектов. Время по Ньютону также считается абсолютным, протекающим равномерно и одинаково во всех системах отсчета.

3.1.Динамика свободной материальной точки

62

3.1.1.Основные законы динамики

1. Закон инерции (первый закон Ньютона)

Изолированная материальная точка находится в состоянии покоя или равномерного прямолинейного движения.

Движение, происходящее с постоянной скоростью в одной системе отсчета, может представляться ускоренным в другой системе отсчета. Системы отсчета, в которых выполняется закон инерции, носят название инерциальных систем отсчета. Гелиоцентрическая система координат (с началом в центре солнца и осями, направленными на «неподвижные» звезды), весьма близка к инерциальной. Легко понять, что все системы отсчета, движущиеся равномерно и поступательно относительно инерциальной системы отсчета, также являются инерциальными, т.к. ускорение точки в этих системах не отличается от ускорения в неподвижной системе отсчета, т.е. равно нулю.

2. Основной закон динамики (второй закон Ньютона)

Сила, действующая на материальную точку, сообщает ей ускорение,

которое в инерциальной системе отсчета пропорционально величине силы и имеет направление силы.

Аналитическое выражение этого закона носит название основного

уравнения динамики

¡ ¢,

F – сила, действующая на точку,

a– ускорение точки, m – масса точки.

3. Закон равенства действия и противодействия (третий закон Ньютона)

Две материальные точки взаимодействуют так, что силы их взаимодействия равны по величине, противоположны по направлению и имеют общую линию действия.

4. Закон независимости действия сил

63

Если на материальную точку действует несколько сил, то ускорение,

приобретаемое точкой, равняется геометрической сумме ускорений,

которые приобрела бы точка под действием каждой силы в отдельности.

¡ ¡A ¡ ¡<,

где ¡A ¢¤{ , ¡ ¢¤. , … , ¡< ¢¤J

или ¡ ∑ ¢¦.

Последнее соотношение носит название основного уравнения динамики точки.

3.1.2. Дифференциальные уравнения движения материальной точки

Если на материальную точку массы m действуют силы ¢A, ¢ ,… , ¢<,

Этому векторному дифференциальному уравнению соответствуют скалярные уравнения, форма которых зависит от выбора системы координат.

Например, в проекциях на оси декартовой системы координат уравнение (1.1) принимает вид:

max = m&x& = Fx , ma y = m&y& = Fy ,

maz = m&z& = Fz .

(1.2)

64

Уравнения (1.2) носят название дифференциальных уравнений движения точки в координатной форме.

В проекциях на оси естественной системы координат, т.е. на касательную, нормаль и бинормаль, дифференциальные уравнения движения точки принимают вид:

0 = Fb .

Уравнения (1.3) носят название дифференциальных уравнений движения точки в естественной форме или в форме Эйлера.

3.1.3.Две задачи динамики

Вдинамике решают две основные задачи, постановки которых мы и рассмотрим. Методика решения каждой из этих задач зависит от способа задания движения точки.

Первая задача динамики

Задача формулируется следующим образом:

найти силу, действующую на точку массой m, движущуюся по

известному закону.

Решение задачи основано на умении находить вектор ускорения a при различных способах задания движения.

Векторный способ задания движения предполагает, что известна зависимость r = r (t).

Чтобы решить поставленную задачу нужно определить ускорение a = dv/dt = d2r/dt2 , а затем с помощью (1.1) – искомую силу F = ma = md2r/dt2.

Координатный способ задания движения предполагает, что известны зависимости:

x = f1(t), y = f2(t), z = f3(t).

65

Дифференцируя их дважды, найдем проекции вектора ускорения на оси координат:

ax = &x& = f1′′(x), ay = &y& = f2′′(x), az = &z& = f3′′(x),

откуда с помощью (1.2) проекции искомой силы: Fx , Fy и Fz , по которым легко найти ее модуль и направление:

F = |F| = Fx2 + Fy2 + Fz2 ,

cos(F,i) = Fx /F, cos(F,j) = Fy /F, cos(F,k) = Fz /F.

Задача 1.1. Найти силу, под действием которой точка массой m движется по закону:

Решение.

Исключив из этих соотношений время t, получим уравнение траектории движущейся точки:

(x/a)2 + (y/b)2 = 1.

Дифференцируя (1), получим:

&x& = −aω 2 cos ωt, &y& = −bω 2 sin ωt.

Подставляя в (1.2), найдем:

Fx = m&x& = −mω 2 x,

Fy = m&y& = −mω 2 y,

F = |F| = 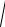Fx2 + Fy2 = mω2r, cos(F, i) = – x/r , cos(F, j) = – y/r,

______

где r = √ x2 + y2 (рис. 1).

66

Рис.3.1

Таким образом, точка движется в плоскости xOy под действием квазиупругой силы F = – mω2r.

Естественный способ задания движения предполагает, что известна траектория и закон движения точки по траектории: s = f(t) .

Чтобы найти действующую на точку силу нужно вычислить проекцию вектора скорости на направление орта касательной:

vτ = ds/dt = s& ,

проекции касательного и нормального ускорений:

aτ = d2s/dt2 = &s&, an = v2/ρ ,

а затем из уравнений (1.3) определить проекции вектора силы на эти направления:

Fτ = maτ и Fn = man .

После этого легко найти ее модуль и направление:

F = |F| = 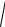Fx2 + Fy2 , cos (F, τ) = Fτ /F, cos (F, n) = Fn /F.

Задача 1.2. Найти силу натяжения нити T и скорость v конического маятника весом P, если нить длиной l образует с вертикалью угол α (рис. 2).

Решение.

Проектируя основное уравнение динамики для нашей задачи:

откуда найдем скорость конического маятника:

_________

v = √gl sinα tgα .

Вторая (основная) задача динамики материальной точки.

Вторая или основная задача динамики является обратной первой. Она формулируется следующим образом: найти закон движения точки массой m, движущейся под действием заданной силы при известных начальных условиях.

Математически поставленная задача сводится к решению системы дифференциальных уравнений второго порядка (1.2):

md2x/dt2 = Fx ,

md2y/dt2 = Fy , (1.4) md2z/dt2 = Fz ,

при заданных начальных условиях:

68

При этом Fx, Fy и Fz в общем случае являются функциями следующих переменных: t, x, y, z, x&, y& , z&.

В следующем параграфе мы рассмотрим решение второй задачи в зависимости от вида этих функций.

3.1.4. Прямолинейное движение точки

Если точка движется вдоль оси Ox, уравнения (1.4) и (1.5) принимают следующий вид:

F = const.

Задача 1.3. Найти максимальную высоту подъема тела массой m, брошенного вверх со скоростью v0 , пренебрегая сопротивлением воздуха.

Решение.

Проектируя основное уравнение динамики

ma = P,

на ось Oy, направленную вверх – по движению точки, получим:

¨'¨# ©,

разделим переменные и проинтегрируем:

Постоянную интегрирования –A 'O определим из начального условия

'"0$ 'O.

В результате получим закон изменения скорости тела:

Рассмотрим (3) и (4) в момент времени t = tпод, соответствующий достижению максимальной высоты подъема H :

0 = v0 – gtпод ;

H = v0tпод + (1/2)g#под.

Из полученной системы уравнений находим высоту подъема тела,

H= v02/(2g).

Вслучае, когда на тело, движущееся прямолинейно, действует сила, зависящая только от времени, F = F(t), интегрирование основного уравнения динамики (1.1) по аналогии с задачей (1.3) дает законы изменения скорости и координаты тела с течением времени:

t

v = v0 + (1/m) ∫ F(t)dt ,

0

t t

x = x0 +v0t + (1/m) ∫(∫ F(t)dt)dt .

0 0