Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Архитектурно-Строительный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3877

.pdf

Скачиваний:

Добавлен:

21.11.2023

Размер:

407.49 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

	Вычислить	интеграл	∫∫∫ f (x, y, z) dx dy dz ,		где	V	–	область,
			V
ограниченная параболоидом			вращения z = x2 + y2, координатными
плоскостями и плоскостью х + у = 2.
8.07	∫∫∫(x2 + y 2 ) dx dy dz		8.08	∫∫∫(2x + 3y) dx dy dz
	V			V
8.09	∫∫∫(x2 y 2 ) dx dy dz		8.10	∫∫∫(x2 + z 2 ) dx dy dz
	V			V
8.11	∫∫∫yz dx dy dz		8.12	∫∫∫xy dx dy dz
	V			V
	Вычислить	интеграл	∫∫∫ f (x, y, z) dx dy dz ,		где	V	–	область,
			V
ограниченная параболическим цилиндром z = 9 – x 2					и плоскостями x = 0,
y = 0, z = 0, 2x + y = 6 (x ≥ 0)
8.13	∫∫∫(x + y) dx dy dz		8.14	∫∫∫ yz dx dy dz
	V			V
8.15	∫∫∫( y + z) dx dy dz		8.16	∫∫∫x2 y2 dx dy dz
	V			V
8.17	∫∫∫z 2 x dx dy dz		8.18	∫∫∫yx2 dx dy dz
	V			V
	Вычислить	интеграл	∫∫∫ f (x, y, z) dx dy dz ,		где	V	–	область,
			V

ограниченная параболическим цилиндром z = 1 y2 и плоскостями 3x + y -

			3
6 = 0, x = 0, y = 0, z = 0
8.19	∫∫∫(xy + z) dx dy dz	8.20	∫∫∫(x + z 2 ) dx dy dz
	V		V
8.21	∫∫∫xz dx dy dz	8.22	∫∫∫x2 y dx dy dz
	V		V
8.23	∫∫∫(x2 + z) dx dy dz	8.24	∫∫∫(x2 + z 2 ) dx dy dz
	V		V
		40

Вычислить	интеграл	∫∫∫ f (x, y, z) dx dy dz ,		где			V –	область,
		V	у =				у = 3

ограниченная параболическими цилиндрами					х	,			х	и
плоскостями	z	=	0							и

x + z = 9

8.25	∫∫∫x2 y dx dy dz	8.26	∫∫∫(x2 + y) dx dy dz
	V		V
8.27	∫∫∫yz dx dy dz	8.28	∫∫∫( y3 + z) dx dy dz
	V		V
8.29	∫∫∫(x + y3 ) dx dy dz	8.30	∫∫∫x2 z 2 dx dy dz
	V		V

§9 Тройной интеграл в цилиндрических и сферических координатах

Для вычисления тройного интеграла часто используются так

называемые цилиндрические координаты.

Положение точки M(x, y, z) в пространстве Oxyz можно определить заданием трёх чисел ρ, φ, z, где

ρ– длина радиуса-вектора проекции точки М на плоскость Оху, ρ ³ 0 ;

φ– угол, образованный этим радиусом-вектором с осью Ох, ϕ [0,2π ];

z – аппликата точки М, z R (рис. 20).

Эти три числа (ρ, φ, z) называются цилиндрическими координатами точки

М.

M(x,y,z)

		•	M(ρ,φ,z)
			M(ρ,φ,z)
			z
φ	ρ		y
φ	ρ
x		•

Рис.20 41

Цилиндрические координаты точки связаны с её декартовыми координатами следующими соотношениями:

		x = ρ cosϕ

		y = ρ sinϕ

		z = z.
Тогда	∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρ cosϕ, ρ sinϕ, z)× ρ × dϕ dρ dz .
	V	V

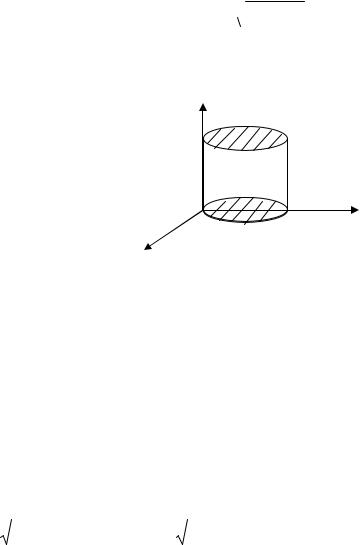
К цилиндрическим координатам бывает удобно перейти в случае, если область интегрирования образована цилиндрической поверхностью.

Пример 1. Вычислить ∫∫∫z x2 + y 2 dx dy dz , если V – цилиндр

х2 + у2 = 2х , ограниченный плоскостями z = 0 , z = a (рис.21).

z = a

Рис.21

x = ρ cosϕ

Решение Перейдём к цилиндрическим координатам = ρ ϕ

. : y sin

z z

Уравнение цилиндрической поверхности примет вид:

ρ 2 cos2 ϕ + ρ 2 sin2 ϕ = 2ρ cosϕ , т.е. ρ = 2cosϕ , где ϕ меняется от - π до

+ π , а ρ меняется от ρ = 0 до			ρ = 2cosϕ .
2
∫∫∫z		dxdydz = ∫∫∫z			× ρ dϕ dρ dz =
∫∫∫z	x2 + y 2	dxdydz = ∫∫∫z		ρ 2 cos2 ϕ + ρ 2 sin 2 ϕ	× ρ dϕ dρ dz =
V		V

		π						2 cosϕ												π				2 cosϕ								a			π			2 cosϕ
	2														a				2										z	2				2						a	2
	2														a				2											2				2							2
= ∫ dϕ ∫ ρ 2 dρ ∫ z dz = ∫ dϕ ∫ ρ 2 dρ																																	= ∫ dϕ ∫						ρ 2 dρ ×			=
= ∫ dϕ ∫ ρ 2 dρ ∫ z dz = ∫ dϕ ∫ ρ 2 dρ																																	= ∫ dϕ ∫						ρ 2 dρ ×			=
	−		π						0						0				−		π			0		2						0		−		π		0	2
			π						0						0						π			0								0				π		0
			2																		2															2
			2																		2															2
					π									2 cosϕ							π											π
		a		2		2					ρ	3				4a		2 2									4a			2		2
				2		2						3						2 2												2		2
=						∫ dϕ									=						∫cos3 ϕ dϕ =											∫cos2 ϕ × cosϕ dϕ =
=						∫ dϕ									=						∫cos3 ϕ dϕ =											∫cos2 ϕ × cosϕ dϕ =
	2				−		π			3				0		3				−		π				3						−	π
							π							0								π											π
							2															2											2
							2															2											2
							π		(1 - sin 2 ϕ )d sinϕ =															2								ϕ			π
		4a			2		2																4a	2				sin			3					2
=		4a					∫																4a		sinϕ	-		sin										=
=																									sinϕ	-											π	=
			3																			3								3							π
								π
							−	2																											−		2



		4a2								1							1					16a2
=							1 −						−		− 1 +				=						.
=				3			1 −						−		− 1 +				=			9			.
				3						3							3					9

Сферическими координатами точки M(x,y,z) пространства Oxyz называется тройка чисел ρ, θ, φ, где

ρ – длина радиуса-вектора точки М, ρ ³ 0 ,


θ –	угол отклонения радиуса-вектора ОМ от оси Oz, 0 ≤ θ ≤ π ,

φ –	угол, образованный проекцией радиуса-вектора ОМ на плоскость
	Ох и осью Ох, 0 £ϕ £ 2π ,	(рис.22).
	z
			M(x,y,z)
	θ	• M(ρ,φ,θ)
	θ	ρ
	φ			у
	φ
	x	•
	x
	Рис.22
Сферические координаты ρ, φ, θ связаны с декартовыми x, y, z
соотношениями:
	x = ρ sinθ cosϕ

	y = ρ sinθ sinϕ

	z = ρ cosθ ;
∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρ cosϕ sinθ , ρ sinϕ sinθ , ρ cosθ )ρ 2 sinθ dρ dϕ dθ .
V	V
		43

Переходить к сферическим координатам удобно, когда область интегрирования есть шар или его часть, а также, если подынтегральная

функция имеет вид f (x2 + y 2 + z 2 ) .

Пример 2. Вычислить ∫∫∫xyz dxdydz ,		если область V – часть сферы
V
x2 + y 2 + z 2 = R 2 , расположенная в I октанте.
z
• R
0•	•	y
	R	y

R • x

Рис.23

Решение. Для вычисления интеграла перейдём к сферическим координатам:

x = ρ sinθ × cosϕ y = ρ sinθ × sinϕ , z = ρ cosθ

где		0 ≤ ρ ≤ R , 0 £ ϕ £ π , 0 £ θ £ π .
Тогда						2			2
Тогда				π	π
				π	π
				2	2	R
∫∫∫xyz dxdydz = ∫dθ ∫dϕ ∫ ρ 3 sin 2 θ × cosϕ sinϕ cosθ × ρ 2 sinθ dρ =
V				0	0	0
π			π								π			π																		R
2			2	R							2			2															ρ		6
2			2	R							2			2																	6
= ∫dθ ∫dϕ ∫sin3 θ cosθ sinϕ cosϕ × ρ 5dρ = ∫dθ ∫sin3 θ cosθ sinϕ cosϕ dϕ																																=
																																=
0			0	0							0			0														6				0
			π		π							θ	π				ϕ	π
	R	6	2		2		R	6		sin	4		2		sin	2		2		R	6		1		1		R	6
=	R		∫sin3 θ d sinθ		∫sinϕ d sinϕ =		R		×	sin			2	×	sin			2	=	R		×	1	×	1	=	R			..
=			∫sin3 θ d sinθ		∫sinϕ d sinϕ =				×					×					=			×		×	2	=				..
6			0		0	6			4				0	2				0	6			4			2	48
			0		0								0					0

Задание № 9

Тело V задано ограничивающими его поверхностями, μ – плотность. Найти массу тела.

9.1	64(x2 + y 2 )= z 2 ,						x2 + y 2 = 4 ,
	y = 0 , z = 0 ( y ³ 0, z ³ 0) ;
	μ = 5(x2 + y 2 )/ 4 .
9.2	x2 + y 2 + z 2 = 4 ,						x2 + y 2 = 1 ,
	(x2 + y 2 ≤ 1),					x = 0 (x ³ 0);
	μ = 4	z	.

9.3	x2 + y 2 = 1 ,					x 2 + y 2 = 2z ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0);
	μ = 10x .
9.4	x2 + y 2 =			16	z 2 ,		x2 + y 2 =	4	z ,

	49						7
	x = 0, y = 0 (x ³ 0, y ³ 0);
	μ = 80 yz .
9.5	x2 + y 2 + z 2 = 1,						x2 + y 2 = 4z 2 ,
	x = 0, y = 0, (x ³ 0, y ³ 0, z ³ 0);
	μ = 20z .
9.6	36(x2 + y 2 )= z 2 ,						x2 + y 2 = 1 ,

x = 0, z = 0 (x ³ 0, z ³ 0);

μ= 5 (x2 + y 2 ). 6

9.7	x2 + y 2 + z 2 = 16 ,			x2 + y 2 = 4 ,
	(x2 + y 2 ≤ 4);
	μ = 2	z	.
	μ = 2	z	.
9.8	x2 + y 2 = 4 , x2 + y 2 = 8z ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0);
				45

μ = 5x .


9.9	x2 + y 2 =			4	z 2 ,		x2 + y 2 =	2	z ,

	25						5
	x = 0, y = 0 (x ³ 0, y ³ 0);
	μ = 28xz .
9.10	x2 + y 2 + z 2 = 4 ,						x2 + y 2 = z 2 ,
	x = 0, y = 0 (x ³ 0, y ³ 0, z ³ 0);
	μ = 6z .
9.11	25(x2 + y 2 )= z 2 ,						x2 + y 2 = 4 ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0, z ³ 0);
	μ = 2(x2 + y 2 ).
9.12	x2 + y 2 + z 2 = 9 ,						x2 + y 2 = 4 ,
	(x2 + y 2 ≤ 4),					y = 0, (y ³ 0,);
	μ =	z	.

9.13	x2 + y 2 = 1 ,					x 2 + y 2 = 6z ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0);
	μ = 90 y .
9.14	x2 + y 2 = z 2 / 25 ,						x2 + y 2 = z / 5 ,
	x = 0, y = 0 (x ³ 0, y ³ 0);
	μ = 14 yz .
9.15	x2 + y 2 + z 2 = 4 ,						x2 + y 2 = 9z 2 ,
	x = 0, y = 0 (x ³ 0, y ³ 0, z ³ 0);
	μ =10z .
9.16	9(x2 + y 2 )= z 2 ,						x2 + y 2 = 4 ,

x = 0, y = 0, z = 0 (x ³ 0, y ³ 0, z ³ 0);

μ = 5(x2 + y 2 )/ 3 .

9.17x2 + y 2 + z 2 = 4 ,

x2 + y 2 = 1 , (x2 + y 2 ≤ 1);

μ = 6 z .

9.18	x2 + y 2 = 1 ,			x2 + y 2 = z ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0);
	μ = 10 y .
9.19	x2 + y 2 = z 2 / 49 ,				x2 + y 2 = z / 7 ,
	x = 0, y = 0 (x ³ 0, y ³ 0);
	μ =10xz .
9.20	x2 + y 2 + z 2 = 4 ,				x2 + y 2 = 4z 2 ,
	x = 0, y = 0 (x ³ 0, y ³ 0, z ³ 0);
	μ =10z .
9.21	16(x2 + y 2 )= z 2 ,				x2 + y 2 = 1 ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0, z ³ 0);
	μ = 5(x2 + y 2 ).
9.22	x2 + y 2 + z 2 = 16 ,
	x2 + y 2 = 4 (x2 + y 2 ≤ 4);
	μ =	z	.

9.23	x2 + y 2 = 4 ,			x 2 + y 2 = 4z ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0);
	μ = 5 y .
9.24	x2 + y 2 = z 2 ,			x2 + y 2 = z ,
	x = 0, y = 0 (x ³ 0, y ³ 0);
	μ = 35 yz .
9.25	x2 + y 2 + z 2 = 1,				x2 + y 2 = z 2 ,
	x = 0, y = 0 (x ³ 0, y ³ 0, z ³ 0);
	μ = 32z .
9.26	x2 + y 2 = z 2 ,			x2 + y 2 = 4 ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0, z ³ 0);
					47

	μ = 5(x2 + y 2 )/ 2 .
9.27	x2 + y 2 + z 2 = 9 ,		x2 + y 2 = 4 ,
	(x2 + y 2 ≤ 4),	z = 0 (z ³ 0);
	μ = 2z .
9.28	x2 + y 2 = 1 ,	x2 + y 2 = 3z ,
	x = 0, y = 0, z = 0 (x ³ 0, y ³ 0);
	μ =15x .
9.29	x2 + y 2 = 4z 2 / 49 ,		x2 + y 2 = 2z / 7 ,
	x = 0, y = 0 (x ³ 0, y ³ 0);
	μ = 20xz .
9.30	x2 + y 2 + z 2 = 16 ,		x2 + y 2 = 9z 2 ,
	x = 0, y = 0 (x ³ 0, y ³ 0, z ³ 0);
	μ = 5z .
9.31	4(x2 + y 2 )= z 2 ,		x2 + y 2 = 1 ,

y = 0, z = 0 (y ³ 0, z ³ 0);

μ = 10(x2 + y 2 ).

Литература

1.Бермант, А.Ф. Краткий курс математического анализа/ А.Ф. Бермант. −

М.: Наука, 1964. −663 с.

2.Данко, П.Е. Высшая математика в упражнениях и задачах. Ч.2/ П.Е. Данко, А.Г. Попов, Т.Я Кожевникова. — М.: Высшая школа, 1980. —365 c.

3.Минорский, В.П. Сборник задач по высшей математике/В.П. Минорский. - М.: Наука, 2004г. - 336 с. с илл.

4.Пискунов, Н.С. Дифференциальное и интегральное исчисления для втузов. Т.2/Н.С. Пискунов. — М.: Наука, 1970. — 310 c.

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.11.2023406.98 Кб13872.pdf
#
21.11.2023407.05 Кб03873.pdf
#
21.11.2023407.2 Кб03874.pdf
#
21.11.2023407.24 Кб13875.pdf
#
21.11.2023407.48 Кб13876.pdf
#
21.11.2023407.49 Кб03877.pdf
#
21.11.2023407.63 Кб03878.pdf
#
21.11.2023407.95 Кб03879.pdf
#
21.11.2023115.53 Кб0388.pdf
#
21.11.2023407.95 Кб13880.pdf
#
21.11.2023408.09 Кб03881.pdf