
3877
.pdf
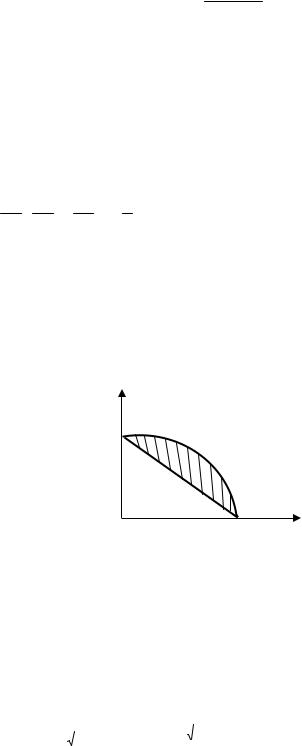
Пример1. Найти массу квадратной пластинки со стороной 2а, если плотность материала пластинки в любой её точке пропорциональна квадрату расстояния от точки пересечения диагоналей до точки М(х,у) и на углах квадрата равна единице.
Решение. Пластинку естественно расположить в прямоугольной системе координат таким образом, чтобы точка пересечения диагоналей совпадала с началом координат, а стороны были параллельны координатным осям
(рис.14).
у
|
а |
|
|
М(х,у) |
|
|
• |
|
|
|
а |
0 |
|
x |
|
|
|
Рис.14
После этого можно составить функцию плотности μ(х, у)материала пластинки по условиям задачи.
Пусть М(х, у) – произвольная точка квадрата ( х ≤ а, у ≤ а). Тогда квадрат расстояния от точки пересечения диагоналей (начала координат)
будет равен ОМ 2 , где ОМ 2 = х2 + у2 . Следовательно, плотность в точке М представится в виде
μ(х, у) = k (x2 + y 2 ),
где k – коэффициент пропорциональности.
Чтобы найти численное значение этого коэффициента k, используем известное значение плотности на углах квадрата. Возьмём, например, вершину угла (а,а). Тогда получим
1 = k (a 2 + a 2 ) ,
откуда
k = 1 . 2a 2
30
Подставляя найденное значение k в выражение функции плотности, окончательно получим
μ(х, у) = х2 + у2 . 2а2
Теперь вычислим двойной интеграл
m = ∫∫μ(x,
|
|
D |
|
|
|
= |
2 |
|
a |
|
|
|
2 |
|
∫ x |
2 |
|
|
a |
|
|
|
|
|
|
|
0 |
|
|
= 2 a 4 a 2 3
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
a |
|
a |
|||
y)dxdy = ∫∫ |
|
|
(x2 + y 2 )dxdy = |
|
|
|
∫dx∫(x2 |
||||||||||||||||||||
2a |
2 |
2a |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y |
3 |
|
|
a |
|
|
|
2 |
a |
2 |
|
a |
3 |
|
|
|
2 |
|
|
x |
3 |
|
||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y + |
|
|
dx = |
|
|
2 |
|
a + |
|
|
|
|
|
2 |
|
|
|
a + |
|||||||||
3 |
|
|
|
a |
∫ x |
|
3 |
dx = |
|
a |
|
|
3 |
||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
+a 4 = 4 a 2 . 3 3
+ y 2 )dy =
a |
3 |
a |
= |
||
|
x |
|
|
||
|
|
||||
3 |
|
|
|
|
|
|
|
0 |
|
||
|
|
||||
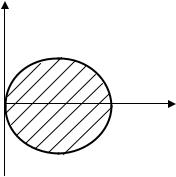
Пример 2. Найти статические моменты относительно осей координат
части эллипса |
x2 |
+ |
y 2 |
= 1, отсекаемой прямой bx + ay = ab (рис.15). |
|
a 2 |
b2 |
||||
|
|
|
у
b
0 |
a |
х |
Рис.15
Решение. В этой задаче о плотности ничего не упоминается. Следовательно, она предполагается постоянной и равной единице, и масса фигуры численно равна её площади. Отсюда получаем
|
|
b |
|
|
|
|
|
|
b |
|
2 |
−x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
a2 −x2 |
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
(a 2 |
− x2 )− |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
a |
a |
a |
y |
2 |
|
|
|
|
|
|
|
|
1 |
a |
2 |
b |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
M x = ∫∫ y dxdy = ∫dx |
|
|
|
|
∫ y dy =∫ |
|
|
|
|
|
|
|
dx |
= |
∫ |
b |
|
|
(a − x)2 |
dx = |
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
||||||||||||||||||
D |
0 |
|
b |
(a−x) |
0 |
2 |
|
|
|
|
|
|
|
|
2 |
0 |
a |
|
|
|
a |
|
|
|
||||||
|
|
|
b |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
(a−x) |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
31

|
1 |
|
|
b2 a |
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
b2 a |
2 |
|
b2 ax2 |
|
x3 |
|
|
a |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= |
|
|
× |
|
|
∫(a |
|
|
- x |
|
|
- a |
|
|
|
+ 2ax - x |
|
)dx = |
|
∫(2ax - 2x |
|
)dx = |
|
|
|
- |
|
|
|
|
= |
||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a 0 |
|
|
a 2 |
|
3 |
|
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
b2 a3 |
|
a3 |
= |
|
ab2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
2 |
|
|
|
3 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a2 −x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
M y |
= ∫∫ x dxdy = ∫ x dx a |
|
|
|
∫dy = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
D |
|
|
|
|
|
|
0 |
|
|
|
|
b |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a−x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a
Пример 3. Найти координаты центра тяжести фигуры, ограниченной двумя параболами у2 = х и х2 = у; μ = 1.
Решение. Для нахождения координат центра тяжести хс и ус достаточно вычислить по заданной области три интеграла, определяющие массу и статические моменты этой области (рис.16).
у
у2 = х
• С
у = х2
0 |
1 |
х |
Рис.16
|
|
1 |
x |
|
|
|
|
1 |
|
|
|
|
|
|
m = ∫∫dxdy = ∫dx ∫ dy = |
, |
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||
|
D |
0 |
x2 |
3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
|
3 |
|
|
||||||
M x |
= ∫∫ ydxdy = ∫dx ∫ ydy = |
|
|
, |
||||||||||
20 |
||||||||||||||
|
D |
0 |
|
x2 |
|
|||||||||
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
3 |
|
|
||||||
M y |
= ∫∫xdxdy = ∫ xdx ∫ dy = |
. |
||||||||||||
20 |
||||||||||||||
|
D |
0 |
|
|
x2 |
|
|
|||||||
|
|
|
|
|
|
|
||||||||
32
координаты центра тяжести равны:
|
|
M y |
3 |
|
|
|
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
9 |
|
|
M |
|
|
|
|
|
|
9 |
|
||
xc |
= |
= 20 |
= |
, |
yc = |
x |
= 20 |
= |
. |
|||||||||||
|
|
|
|
|||||||||||||||||
m |
20 |
|
|
20 |
||||||||||||||||
|
|
|
1 |
|
|
|
|
m 1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|||||||
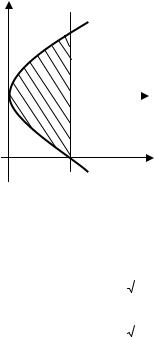
Пример 4. Найти моменты инерции I0 круга радиуса R с центром в точке С(R, 0) относительно точки, лежащей на окружности и совпадающей с началом координат (рис.17).
Решение. Уравнение окружности, соответствующее условию задачи имеет вид:
x2 + y 2 = 2Rx
у
|
• |
|
R |
2R |
x |
|
Рис.17 |
Найдём момент инерции |
I0 = ∫∫(x2 + y2 )dx dy . |
|
D |
Перейдём к полярной системе координат. Уравнение данной окружности в полярной системе координат запишется в виде ρ = 2R cosϕ . Получим
|
|
|
π |
|
|
2 R cosϕ |
|
|
π |
|
|
|
|
|
|
π |
|
|
|
||
|
|
|
|
2 dϕ |
|
|
2 |
ρ 4 |
|
2R cosϕ dϕ = |
1 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
I0 |
= 2 |
|
|
ρ |
3dρ = 2 |
|
16R4 cos4 ϕ dϕ = |
||||||||||||||
|
∫ |
∫ |
4 |
|
∫ |
||||||||||||||||
|
|
|
∫ |
|
|
|
|
|
|
0 |
|
2 |
|
|
|
||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
4 |
2 |
1 + cos 2ϕ 2 |
|
|
|
|
4 |
2 |
|
|
|
2 |
|
||||||
= |
8R |
|
|
∫ |
|
|
|
|
dϕ |
= 2R |
|
∫(1 + 2cos 2ϕ + cos |
|
2ϕ )dϕ = |
|||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
4 |
2 |
|
|
|
|
1 + cos 4ϕ |
|
|
4 |
1 |
|
1 |
|
|
|
||||||
= 2R |
|
∫ |
1 + 2cos 2ϕ + |
|
|
|
|
dϕ |
= 2R |
ϕ + sin 2ϕ + |
|
ϕ + |
|
sin 4ϕ |
|
2 = |
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
8 |
|
|
0 |
|
||
= 2R4 × |
3 π |
= |
3πR4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 5. Вычислить момент инерции области, ограниченной |
|
|
|
|||||||||||||||||||
параболой у2 = ах и прямой х = а относительно прямой |
|
у = −а (рис.18). |
|
|||||||||||||||||||
Решение. |
Чтобы воспользоваться формулой для вычисления момента |
|||||||||||||||||||||
инерции относительно оси х, сделаем преобразование координат: х |
′ |
= х |
, |
|||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
′ |
′ |
|
|
|
|
|
|
|
у′ = у + а |
|
||||
|
|
|
|
|
|
|
|
уравнение параболы примет вид: |
|
|
|
|
|
|
||||||||
тогда в новой системе х Оу |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(у′ − а)2 = ах′ . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
у', у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у2 = ах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М(х, у) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
D |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ау = -а
0' |
х´ |
Рис.18
Следовательно,
|
a |
a+ |
ax |
|
||
I x′ = ∫∫( y¢)2 dx¢dy¢ = ∫dx¢ ∫ |
|
( y¢)2 dy¢ = |
8 |
a4 . |
||
|
||||||
D′ |
|
|
|
5 |
|
|
0 |
a− |
|
|
|||
ax |
||||||
Задание №7
34
7.01Найти массу круга радиуса R, плотность которого в каждой точке равна расстоянию от этой точки до контура круга.
7.02Найти координаты центра тяжести одной четверти круга радиуса R, плотность которого в каждой точке равна расстоянию от этой точки до контура круга.
7.03Найти координаты центра тяжести однородной пластинки, ограниченной линиями у = х2 , у + х = 2 , у = 0 .
7.04Найти статический момент однородного прямоугольника со сторонами а и b относительно стороны а, считая, что прямоугольник лежит в плоскости хОу (начало координат поместить в одну из вершин прямоугольника, а ось Ох направить по стороне а).
7.05Найти момент инерции круга радиуса а относительно центра, считая, что центр находится в начале координат (μ = 1).
7.06 Найти координаты центра тяжести плоской однородной пластинки, ограниченной линиями у = 4 − х2 , у + 2х = 4 .
7.07Найти координаты центра тяжести плоской однородной пластинки, ограниченной окружностью х2 + у2 = 4 и линиями у = 0 , у = х .
7.08Найти момент инерции прямоугольника ОАСВ со сторонами ОА = 4, ОВ =2 относительно вершины О, если плотность его пропорциональна расстоянию до стороны ОВ, считая, что прямоугольник лежит в плоскости хОу (k – коэффициент пропорциональности).
7.09 На фигуре, ограниченной эллипсом |
x2 |
+ |
y 2 |
= 1 распределена масса |
|
a 2 |
b2 |
||||
|
|
|
так, что плотность её пропорциональна расстоянию от оси абсцисс, причём при у = 1 она равна γ. Найти массу фигуры.
7.10Найти координаты центра тяжести однородной пластинки, ограниченной линиями у = 2х − 1, у2 = х, у = 0 .
7.11Найти момент инерции круга радиуса R относительно диаметра, считая, что круг лежит в плоскости хОу (ось Ох направить по диаметру); μ =1.
35
7.12 Найти массу прямоугольной фигуры, ограниченной прямыми х = 0 , х = 2 , у = 0 , у = 3, если плотность в каждой точке равна кубу абсциссы,
умноженному на квадрат ординаты этой точки.
7.13 Найти координаты центра тяжести однородной пластинки, ограниченной линиями у = х2 , у = 3х2 , у = 3х.
7.14Найти момент инерции квадрата со стороной а, поверхностная плотность которого пропорциональна у, относительно одной из вершин, считая, что квадрат находится в плоскости хОу (поместить начало координат в одну из вершин, а координатные оси Ох и Оу направить по двум взаимно перпендикулярным его сторонам. Тогда искомый момент инерции будет равен моменту инерции квадрата относительно начала координат). Коэффициент пропорциональности – k.
7.15Определить центр тяжести однородной пластинки, ограниченной кардиоидой ρ = а(1 + cosϕ) .
7.16Найти статический момент однородного круга радиуса а относительно касательной, считая, что круг лежит в плоскости хОу и касается оси Ох
вначале координат.
7.17Найти момент инерции прямоугольника ОАСВ со сторонами ОА=а и ОВ=b относительно стороны ОВ, если плотность его пропорциональна расстоянию до стороны ОВ, считая, что прямоугольник лежит в плоскости хОу, а одна из его вершин находится в начале координат;
μ= kx , k – коэффициент пропорциональности.
7.18Найти координаты центра тяжести плоской фигуры, ограниченной параболой у = 2х − 3х2 и осью Ох.
7.19Найти статические моменты относительно координатных осей части
плоскости, ограниченной линиями у = х2 , у + х = 2 , у = 0 , |
μ =1. |
7.20 Вычислить момент инерции треугольника, ограниченного |
прямыми |
х + у = 2 , х = 2 , у = 2 относительно оси Ох(μ = 1) . |
|
7.21Найти координаты центра тяжести однородной пластинки, ограниченной параболой у2 = 4х и прямой х = 2 .
36
7.22Найти статические моменты относительно координатных осей четверти круга радиуса R.
7.23Пластинка имеет форму прямоугольного треугольника с катетами
ОВ = а и AO = b , причем плотность её в любой точке равна расстоянию точки от катета ОА (лежащего на оси Ох). Найти статические моменты пластинки относительно катетов ОА и ОВ.
7.24Вычислить координаты центра тяжести площади, ограниченной кривой y = sin x и прямой ОА, проходящей через начало координат и вершину
=π синусоиды
А, 1 .2
7.25Найти моменты инерции кругового кольца с диаметрами d и D (d < D): а) относительно его центра и б) относительно его диаметра.
7.26Найти массу круглой пластинки радиуса R, если плотность её пропорциональна расстоянию точки от центра и равна δ на краю пластинки.
7.27Найти координаты центра тяжести кругового сектора радиуса а с углом при вершине 2α (μ = 1) и осью симметрии Ох.
7.28Плоское кольцо ограничено двумя концентрическими окружностями, радиусы которых равны R и r (R > r). Зная, что плотность материала обратно пропорциональна расстоянию от центра окружностей, найти массу кольца. Плотность на окружности внутреннего круга равна единице.
7.29Вычислить координаты центра тяжести площади, ограниченной
параболами у2 = 4х + 4 , у2 = −2х + 4 , μ =1.
7.30Вычислить момент инерции фигуры, ограниченной линиями у = 4 − х2 ,
у= 0 относительно оси Ох (μ = 1).
§ 8. Вычисление тройного интеграла в прямоугольных координатах
37

Вычисление тройного интеграла так же, как и двойного, производится путем сведения его к последовательному вычислению трех определенных интегралов. При этом удобнее сначала представить его в виде комбинации двойного интеграла и внутреннего определенного интеграла. Вычисляя внутренний интеграл, сведём дальнейшее
интегрирование к вычислению |
двойного интеграла уже известным |
|
способом. Например: |
|
|
|
|
z2 ( x, y ) |
∫∫∫ f (x, y, z)dxdydz = ∫∫dxdy |
∫ f (x, y, z)dz , |
|
T |
D |
z1 ( x, y ) |
где D - проекция пространственной области Т на плоскость хОу. Относительно выбора порядка интегрирования справедливыми
остаются замечания, высказанные для двойного интеграла.
Пример. |
Вычислить |
∫∫∫xyz dx dy dz , |
где V |
- пирамида OPQR, |
|
|
V |
|
|
ограниченная следующими плоскостями: x = 0, |
y = 0, |
z = 0, x + y + z = 1 |
||
(рис.19). |
|
|
|
|
Решение. |
Проекция области V на координатную плоскость Оху есть |
|||
треугольник D, ограниченный прямыми: х = 0, у = 0, х + у = 1. |
||||
При (x, y) D аппликаты точек (x, y, z) V удовлетворяют неравенству |
||||
0 ≤ z ≤ 1 – x - y . |
Тогда |
|
1−x− y |
|
|
|
|
|
|
|
∫∫∫xyz dx dy dz = ∫∫dxdy |
∫ xyz dz . |
||
|
V |
D |
0 |
|
z
|
R • |
|
|
|
|
|
x+y+z=1 |
|
|
|
V |
|
|
|
|
• |
N(x,y,z) |
|
|
|
0 |
|
• |
|
|
D • |
|
||
|
Q(0;1;0) |
y |
||
• |
M(x,y,0) |
|
|
|
P(1;0;0)
x
Рис.19
38
Так как проекцией V на плоскость хОу является треугольник D, то при постоянном х переменная у изменяется от 0 до (1 – х), наконец, х изменяется от 0 до 1. Следовательно,
|
1 |
1−x |
1−x− y |
1 |
1−x |
z |
2 |
|
1− x− y |
|
|
|
|||||||||
∫∫∫xyz dx dy dz = ∫dx ∫ dy |
∫ |
|
|
|
|
|
|
|||
|
|
|
|
|
||||||
xyz dz = ∫dx ∫ xy |
2 |
|
|
dy = |
||||||
V |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
||
|
|
|||||||||
|
|
1 |
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1−x |
|
|
|
|
|
|
|
|
|
|||||
= |
1 |
|
∫dx ∫ xy(1 - x - y)2 dy = |
1 |
|
∫dx ∫ xy[(1 - x)2 - 2(1 - x) y + y 2 ]dy = |
||||||||||||||||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
∫dx ∫ x[(1 - x)2 y - 2(1 - x) y 2 + y3 ]dy = |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
1 |
|
|
|
|
|
2 |
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
|
|
|
y 4 |
|
1−x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
(1 - x) |
|
|
× |
|
|
|
- 2(1 - x) × |
|
|
|
|
+ |
|
|
|
|
|
|
dy = |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
∫ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
4 |
|
1 |
|
2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
4 |
|
|
|
||||||||||
= |
|
|
∫ x × (1 - x) |
|
|
× |
|
|
- |
|
+ |
|
|
|
dx |
= |
|
|
|
|
|
∫ x(1 - x) |
|
dx = |
||||||||||||||||||||
2 |
|
|
3 |
|
|
24 |
|
|
||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|||
= |
∫(1 - (1 - x)) × (1 - x)4 dx = |
|
|
|
∫(1 - x)4 dx - |
∫(1 - x)5 dx = |
||||||||||||||||||||||||||||||||||||||
24 |
24 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
24 |
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= - |
|
(1 - x)5 |
|
+ |
|
(1 - x)6 |
|
1 |
= |
|
1 |
|
|
- |
|
|
1 |
|
= |
|
1 |
. |
|
|
|
|
||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
24 |
× 5 |
|
0 |
24 × 6 |
|
0 |
120 |
|
144 |
720 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание №8
|
Вычислить интеграл |
∫∫∫ f (x, y, z) dx dy dz , где V – область, |
|
|
|
V |
|
ограниченная плоскостями y = x, y = 1, z = 0, x + y + z = 4. |
|||
8.01 |
∫∫∫xy dx dy dz |
8.02 |
∫∫∫(x + y) dx dy dz |
|
V |
|
V |
8.03 |
∫∫∫xz dx dy dz |
8.04 |
∫∫∫(x + z) dx dy dz |
|
V |
|
V |
8.05 |
∫∫∫ yz dx dy dz |
8.06 |
∫∫∫( y + z) dx dy dz |
|
V |
|
V |
|
|
39 |
|
