
3553
.pdf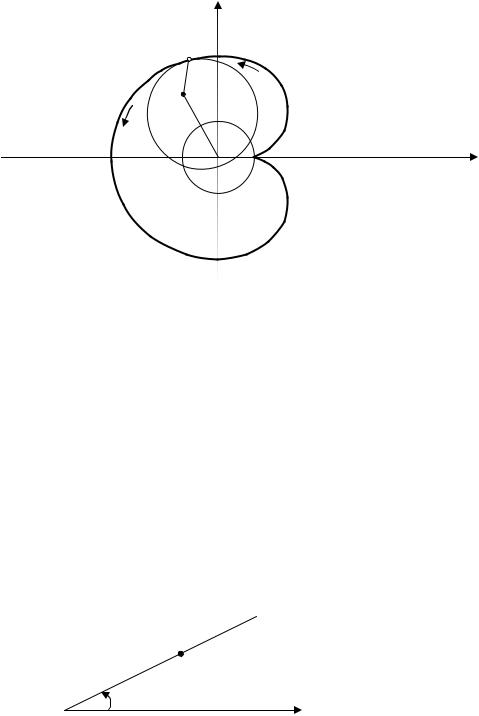
y
M (x, y)
O |
a |
x |
Рис. 21.
x = a(2cost − cos 2t ) |
, 0 £ t £ 2π . |
Уравнения кардиоиды |
|
y = a(2sin t − sin 2t ) |
|
§ 8. Кривые в полярной системе координат.
Рассмотрим полярную систему координат на плоскости. Пусть нам задан полюс и полярная ось. Для произвольной точки M на плоскости обозначим через ρ расстояние от точки O до точки M , а через ϕ – угол, на который нужно повернуть полярную ось до совмещения с лучом.
М
ρ
ϕ
О |
Р |
|
Рис. 22.
Числа ϕ , ρ называются полярными координатами точки M . Число ρ называют полярным радиусом (всегда ρ ³ 0 ), а число ϕ называют полярным углом точки M . Полярный радиус для любой точки определяется однозначно, а полярный угол – с точностью до 2π n , где n – целое число.
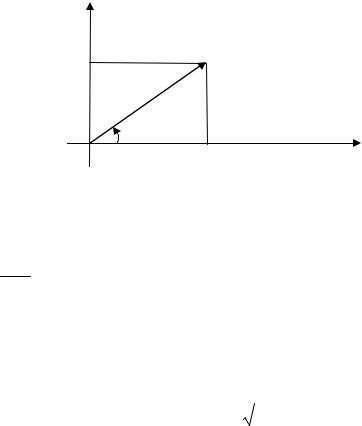
Пусть на плоскости задана полярная и правая декартова прямоугольная система координат.
y
y |
M |
|
|
|
|
|
ρ |
|
ϕ |
|
|
0 |
x |
x |
|
||
Рис. 23. |
|
|
Пусть M |
– произвольная точка плоскости, имеющая декартовы |
|
координаты (x, y) и полярные координаты (ϕ, ρ). Рассмотрим радиус вектор
OM точки M . Сравнивая |
координаты, получим формулы перехода от |
||||||||
декартовых координат к полярным: |
|
|
|
||||||
|
x = ρ cos ϕ , |
y = ρ sinϕ . |
|||||||
Формулы перехода от полярных координат (ϕ, ρ) к декартовым (x, y) |
|||||||||
можно записать в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
tgϕ = |
y |
(x ¹ 0). |
||||
ρ = |
x2 + y 2 |
, |
|||||||
|
|||||||||
|
|
|
|
|
|
|
x |
||
При x = 0 можно вычислить |
ctgϕ = |
x |
. |
|
|
|
|||
|
|
|
|
||||||
|
|
|
y |
|
|
|
|||
Кривую в полярных координатах задают в виде уравнения
или явного уравнения в виде ρ = f (ϕ).
Рассмотрим несколько примеров кривых, заданных в координатах.
F (ϕ, ρ)= 0
полярных
9.Уравнение ρ = a , где a – постоянное число, задает окружность радиуса a , центр которой совпадает с полюсом O .
10.Уравнение ϕ = t определяет луч, исходящий из полюса и составляющий угол t с полярной осью. t – произвольное число.
11.Выведем полярное уравнение окружности радиуса R в случае, когда полюс лежит на ней, а полярная ось проходит через центр окружности.

M
ρ
ϕ N
O R |
R |
p |
Рис. 24.
Возьмем произвольную точку M на окружности. Треугольник OMN прямоугольный. Получаем уравнение окружности в виде ρ = 2R cosϕ .
12.Покажем, что уравнение ρ = 2a sinϕ и полярных координатах
определяет окружность радиуса a . Подставим выражения для ϕ и ρ через x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||
и y |
в уравнение: |
x2 + y 2 |
= 2a × |
|
|
|
|
. Умножая обе части уравнения на |
||||||||||||||
|
|
|
|
|
||||||||||||||||||
x |
2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x2 + y 2 = 2ay |
|
|
|
x2 + (y - a)2 = a2 . |
|
|
|
||||||||
|
x2 |
+ y 2 |
, |
получим |
или |
|
|
Это уравнение |
||||||||||||||
окружности радиуса |
|
a |
|
с центром в точке (0, a). |
прямые x = a , |
|||||||||||||||||
|
|
|||||||||||||||||||||
|
|
13. |
Пусть в |
|
|
декартовой системе |
|
координат заданы |
||||||||||||||
y = b . Уравнения этих прямых в полярной системе координат ρ = |
a |
|||||||||||||||||||||
|
, |
|||||||||||||||||||||
cosϕ |
||||||||||||||||||||||
ρ = |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sinϕ . |
Рассмотрим уравнение ρ = a sin 3ϕ , a > 0 . Переход к декартовым |
|||||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
14. |
||||||||||||||||||||
координатам здесь довольно громоздкий и приводит к алгебраическому уравнению высокой степени. Поэтому посмотрим эту кривую, исходя из качественных соображений.
|
2π |
|
|
|
|
Период правой части уравнения равен |
|
, поэтому |
достаточно |
||
3 |
|||||
|
|
|
|
2π |
|
построить кривую для значений полярного угла из интервала |
0, |
|
. По |
||
|
|||||
|
|
|
|
3 |
|
свойствам функции ρ = a sin 3ϕ , см. |
рис. 22, видно, что полярный радиус |
||||
ρ монотонно возрастает при 0 £ ϕ £ π |
и при ϕ £ π |
монотонно убывает. При |
|||
π £ ϕ £ |
2π |
6 |
3 |
|
|
|
правая часть уравнения |
ρ = a sin 3ϕ |
отрицательна, для этих |
||
3 |
|
||||
3 |
|
|
|||
значений |
ρ точек кривой нет. Для остальных значений кривая получается |
||||

при повороте на угол |
2π n |
(n =1,2) |
части кривой, расположенной между |
|
3 |
||||
|
|
|
лучами |
ϕ = 0 и ϕ = 2 |
π |
, рис. 24. |
|
|||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2π |
a |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
O |
π |
π |
π |
2π |
ϕ |
O |
|
|
|
|
|
|
|
|
|
|
6 |
3 |
2 |
|
3 |
|
|
− a 
Рис. 25.
Задание 3.
Построить кривые в полярной системе координат.
3.01. ρ = 4sin 2ϕ 3.02. ρ = 2(1 + sinϕ) 3.03. ρ = 3cos3ϕ 3.04. ρ = 2sin 2 2ϕ 3.05. ρ = 3cos2 2ϕ 3.06. ρ = 4cos 2ϕ 3.07. ρ = 3(1 − cosϕ)
3.08. ρ = 2(cosϕ + sinϕ) 3.09. ρ = 6(sinϕ − cosϕ) 3.10. ρ = 4cos2 ϕ
3.11. ρ = |
3 |
|
|
sinϕ |
|||
|
|||
3.12. ρ = |
5 |
|
|
cosϕ |
|||
|
|||
3.13. ρ = |
3(1 − sinϕ) |
|||
3.14. |
ρ = |
3 |
|
|
|
|
|||
8cos 2ϕ |
||||
|
|
|||
π
3 π
6

3.15. |
ρ = |
|
3 |
|
|
5sin 2ϕ |
|||||
|
|
||||
3.16. |
ρ = |
|
6 |
|
|
|
|
|
|||
|
− cosϕ |
||||
|
1 |
||||
3.17.ρ = 3 − 4cosϕ
3.18.ρ = 4 − 2sin 2ϕ
3.19.ρ = 3 + cos 2ϕ
3.20.ρ = 2 − sin 3ϕ
3.21.ρ = 3 + 2cos 2ϕ
3.22.ρ = 4 − 2sin 3ϕ
3.23.ρ 2 = 4cos 2ϕ
3.24.ρ = 2(1 + 2cosϕ )
3.25.ρ 2 × sin 2ϕ = 4
3.26.ρ × cosϕ = 25
3.27.ρ = 2 - 2cosϕ
3.28.ρ =1 + cos 2ϕ
3.29.ρ = 2 + cosϕ
3.30.ρ = 3 - sin 2ϕ1
§ 9. Поверхности второго порядка
Цилиндрические поверхности с образующими, параллельными координатным осям.
Цилиндрической поверхностью называется поверхность, образованная движением прямой, пересекающей заданную линию и параллельной заданному направлению. Заданная линия называется направляющей, а совокупность параллельных прямых – образующими.
Уравнение F (x, y) = 0 задает цилиндрическую поверхность с образующей, параллельной оси oz и направляющей – кривой F (x, y) = 0 в плоскости xoy .
Уравнение F (x, z) = 0 задает цилиндрическую поверхность с образующей, параллельной оси oy и направляющей – кривой F (x, z) = 0 в плоскости xoz .
Уравнение F (z, y) = 0 задает цилиндрическую поверхность с образующей, параллельной оси oz и направляющей – кривой F (z, y) = 0 в плоскости zoy .
Уравнение |
|
x2 |
+ y 2 = R2 |
задает круговой цилиндр |
с |
образующей |
||||||||||||
параллельной оси |
oz |
и |
направляющей – окружностью |
x2 |
+ y 2 = R2 в |
|||||||||||||
плоскости xoy . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение |
|
x2 |
+ |
|
y 2 |
=1 задает эллиптический цилиндр. |
|
|
||||||||||
|
a2 |
b2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Уравнение y 2 |
= 2 px задает параболический цилиндр. |
|
|
|||||||||||||||
Уравнение |
|
x2 |
− |
y 2 |
|
=1 задает гиперболический цилиндр. |
|
|||||||||||
|
a2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
||||
2. |
|
Поверхности второго порядка, заданные своими каноническими |
||||||||||||||||
уравнениями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
x2 |
+ |
y 2 |
+ |
|
z 2 |
=1 – |
эллипсоид |
|
|
|
|||||||
a2 |
b2 |
c2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− a |
|
|
|
|
|
|
−b |
|
|
|
|
|
a |
|
0 |
b |
y |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− c |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||
При a = b = c |
|
|
|
x2 |
+ y 2 + z 2 |
= a2 – сфера |
|
|
|
|||||||||
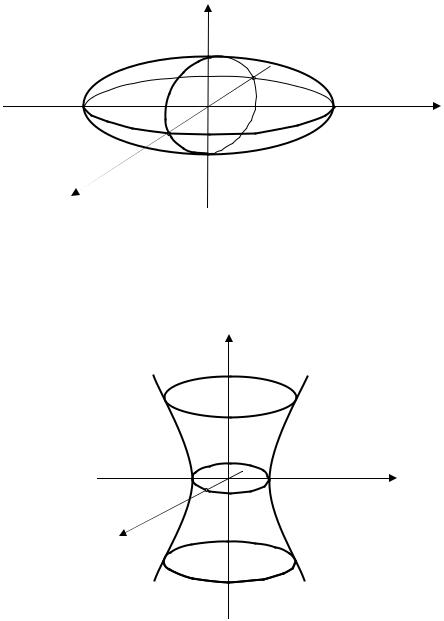
2. |
x2 |
+ |
y 2 |
− |
z 2 |
=1 – |
однополостный гиперболоид |
|
|
|||||||||
a2 |
b2 |
|
|
|
||||||||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|||
z
b o 
a |
y |
x
Рис. 27.
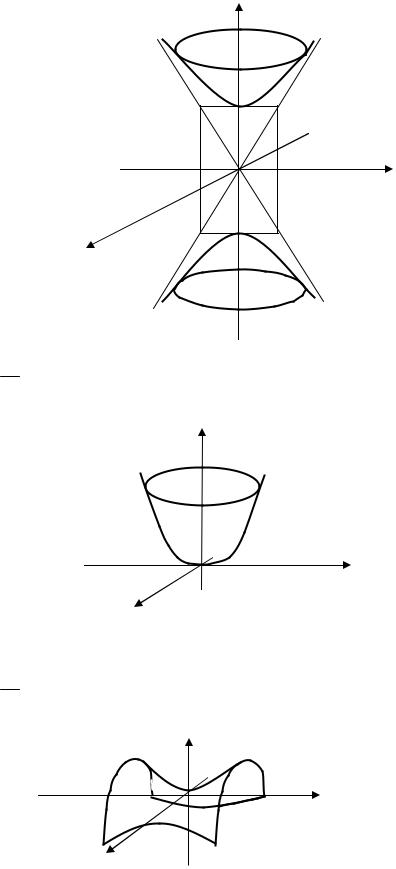
3. |
x2 |
+ |
y 2 |
− |
z 2 |
= −1 – двуполостный гиперболоид |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
z
-b
x
Рис. 28.
x2
4.
p
Рис. 29.
x2
5.
p
Рис. 30.
+ |
y 2 |
= 2z , p × q > 0 – |
|
q |
|||
|
|
|
|
x |
|
|
+ |
y 2 |
= 2z , p × q < 0 |
– |
|
q |
||||
|
|
|
x
c
0 b |
y |
− c
эллиптический параболоид
z
(p > 0, q > 0)
O |
y |
гиперболический параболоид
z
(p > 0, q < 0)
y

6. |
x2 |
+ |
y 2 |
= |
z 2 |
– конус второго порядка |
a2 |
b2 |
c2 |
z
y
x
Рис. 31.
Задание 4
Определить виды поверхностей и изобразить их. 4.01.
1.3x2 + 4 y 2 − z 2 = 12
2.z 2 − 2x + 4 = 0
3.x2 + 2x + y 2 = 0
4.02.
1.x2 − 3y 2 + z 2 = −6
2.2 y 2 − 4 y + x + 1 = 0
3.x2 − 2 y 2 + z 2 = 0
4.03.
1.2x2 + 4 y 2 + z = 1
2.2x2 + 4x + 3y 2 = 0
3.z + 4 + y 2 + 2 y = 0
4.04.
1.2x2 − 4 y 2 + z 2 = 4
2.3y2 + 6 y + z − 1 = 0
3.x2 + y 2 = 2 y
4.05.
1.3x2 + 4z 2 + y = 3
2.x2 + 3y 2 − z 2 = −6
3.2 y 2 + y − z + 4 = 0
4.06.
1.3x2 + 4z − 5 = 0
2.x2 + y 2 + z 2 − x = 0
3.y 2 − x2 + 2z 2 = 0
4.07.
1.x2 + 2x + y 2 + z 2 = 1
2.y 2 + 2 y + z 2 = 1
3.z + 4 − x2 + x = 0
4.08.
1.2 y + 1 + x2 = 2x
2.y 2 − x2 + 2z 2 = −4
3.2x2 + 4 y 2 + 8z 2 = 1
4.09.
1.3x − 1 + y 2 = − y
2.2x2 − 3y 2 = 16
3.z 2 − x2 + 2 y2 − 4 = 0
4.10.
1.2z + 4 + x2 = 2x
2.x2 + 2 y 2 = 1
3.2x2 + 4 y 2 + z 2 = 4
4.11.
1.2z − 3 − x2 + 4x = 0
2.x2 − 2 y 2 = 2x
3.3x2 − y 2 − z 2 = 6
4.12.
1.2 y + 3 + z 2 − 2z = 0
2.3y2 + 4z 2 = x − 4
3.z 2 + z + y 2 − 2 y = 1

4.13.
1.2x2 + 6 y 2 = 3z
2.x2 − 2x − 2 y 2 + 4 y = 0
3.3x2 + 2 y 2 − z 2 = 1
4.14.
1.3x2 − y 2 + 6z 2 = 12
2.x2 − 2x + 2 y 2 = 0
3.3x + 2 + y 2 + 2 y = 0
4.15.
1.z = 3
 y + 1
y + 1
2.3x2 + y 2 − 3z 2 = −6
3.y 2 + 2 y + z 2 = 1
4.16.
1.y = −
 3x + 1
3x + 1
2.x2 + 2 y 2 + z 2 = 8
3.z 2 − 2 y 2 + 4 = 0
4.17.
1.y 2 + 2 y + z 2 = x − 4
2.3x2 + 4z 2 = 1
3.2x + 1 + y 2 = 0
4.18.
1.3y + 4 − z 2 = 0
2.x2 + 2x − z 2 = 1
3.2x2 − y 2 − z 2 = 4
4.19.
1.− x2 + 2x + z = 1
2.x2 − 2 y 2 + z 2 = −4
3.3y2 + 4z 2 = 1
4.20.
1.2x2 + 4 y 2 = 8z
2.x2 − 3z 2 = 6
3.y + z 2 − 2z = 0
