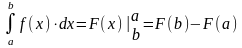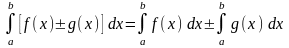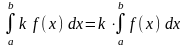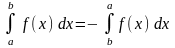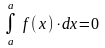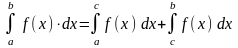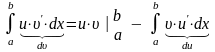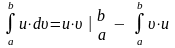Связь между интегралом и первообразной. Формула ньютона-лейбница.

Если известна хотя бы одна первообразная подынтегральной функции, то определенный интеграл можно вычислить без интегральных сумм и предельного перехода с помощью формулы Ньютона-Лейбница.

где

а и b

-

нижний и верхний пределы интегрирования;

F(x)

-

первообразная функции;

F(b)-F(a)

-

приращение первообразной.

Правило вычисления интеграла по формуле Ньютона-Лейбница

Найти неопределенный интеграл от данной функции и из результата подстановки верхнего предела в первообразную функцию ВЫЧЕСТЬ результат подстановки нижнего предела.

1

Интеграл от суммы функции равен сумме интегралов от всех слагаемых

2

Постоянный множитель можно выносить за знак интеграла

3

При перестановке пределов изменяется знак интеграла

4

Интеграл с одинаковыми пределами равен нулю

5

где a < c < b

Отрезок интегрирования можно разбивать на части

Непосредственное интегрирование определенного интеграла состоит в том, что путем тождественных преобразований и применения свойств определенного интеграла приводится к одному или нескольким табличным интегралам, которые вычисляются по формуле Ньютона-Лейбница.

Интегрирование методом введения новой переменной состоит в следующем:

1. часть подынтегральной функции заменить новой переменной так, чтобы затем получить табличный интеграл;

2. найти дифференциал от обеих частей замены;

3. найти новые пределы интегрирования определенного интеграла;

4. всё подынтегральное выражение выразить через новую переменную, после чего получится табличный интеграл;

5. вычислить полученный определенный интеграл, используя новые пределы интегрирования.

Интегрирование по частям осуществляется по формуле: