Интегральная и дифференциальная функции распределения непрерывной случайной величины.

Для описания непрерывной случайной величины пользуются двумя функциями: интегральной функцией распределения и дифференциальной функцией распределения, или плотностью вероятности. Поясним эти понятия на примере результатов измерения некоторой величины, например, длины отрезка. Будем обозначать эту величину a.

Так как результат измерения зависит от огромного числа мелких помех, то при одинаковых макроскопических условиях опыта (те же приборы и метод) измерение – это случайное событие, а результат измерения величины a – это непрерывная случайная величина X, которая в зависимости от сочетания многих причин может принимать непрерывный ряд значений.

Пусть измерение величины a выполнили N раз, причем N’ раз получились значения X<x. Тогда N’/N – это относительная частота появления значений величины X меньших, чем x. При достаточно большом числе опытов N относительная частота становится устойчивой. В этом случае она принимается за приближенное значение вероятности того, что случайная величина X меньше x и обозначается P(X<x). Эта вероятность является функцией величины x:

. (2)

Функция F(x) называется интегральной функцией распределения случайной величины X. F(x) – безразмерная функция. При изменении x от - до + F(x) монотонно возрастает от 0 до 1. Характер возрастания различен для разных случайных величин.

Плотностью вероятности или дифференциальной функцией распределения называется производная от интегральной функции распределения F(x) по переменной x:

. (3)

Так как F(x) = P(X < x + x) – P(X < x)= P(x < X <x + x) – это вероятность того, что значение X лежит между x и x+x, то плотность вероятности – это предел отношения вероятности попадания значений в некоторый интервал к величине интервала, когда последний стремится к нулю. Дифференциальная функция распределения имеет размерность, обратную размерности случайной величины.

Очевидно, интегральная вероятность F(x) может быть выражена интегралом от плотности вероятности

. (4)

Для многих случайных величин, в том числе для случайных результатов измерения, справедлив нормальный закон распределения, или закон Гаусса. В этом случае дифференциальная функция распределения имеет вид

, (5)

г

W(x)

де a и  – постоянные величины.

Рис. 2.

W_max

2 

a

x

x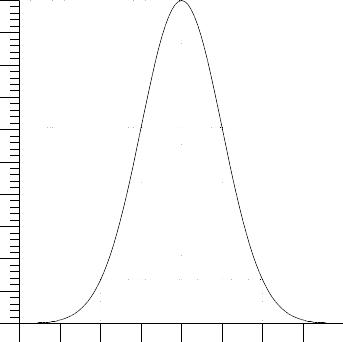

Кривая, изображающая функцию W(x), показана на рис.2. Это колоколообразная кривая с крыльями, прижимающимися к оси абсцисс. При x = a функция W(x) имеет максимум и равна . Значение a называется наиболее вероятным. При x = a   плотность вероятности равна .

Отмеченная на рис. 2 площадка S с основанием x изображает вероятность P попадания случайной величины X в интервал значений x. Так как S = W(x) x, где W(x) – плотность вероятности на интервале x, то случайная величина чаще принимает значения, лежащие в интервалах с большими W(x). Полная площадь под кривой W(x) – это вероятность появления какого-нибудь значения x. Она равна единице.

Интегральная функция распределения, соответствующая плотности вероятности (5), имеет вид

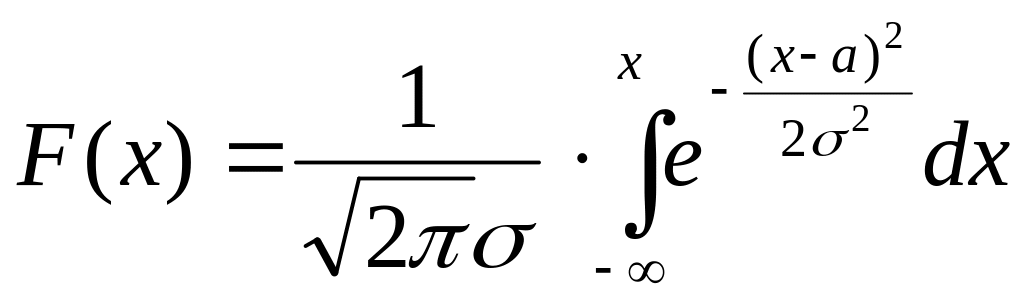. (6)

И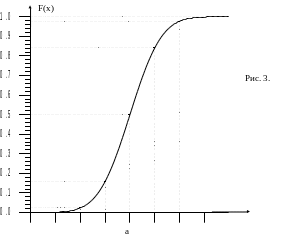 нтеграл (6) не выражается через элементарные функции. Для него составлены таблицы, по которым и построен график функции F(x), изображенный на рис. 3.

И

x

нтегральная функция F(x) = P(X<x) имеет одинаковый смысл как для дискретной, так и для непрерывной случайной величины. Распределение дискретной случайной величины можно описывать также и функцией плотности вероятности, если число возможных значений этой величины велико и вероятность соседних значений отличается незначительно.