
Образцы решений некоторых типовых задач
Пример 1 Решить
систему уравнений методом Крамера и с
помощью обратной матрицы:

Решение 1) Решим систему методом Крамера. Для этого найдем определитель матрицы системы:
 .
Т.к.
.
Т.к.
![]() ,
то решение системы существует и
единственно. Найдем определители
,
то решение системы существует и
единственно. Найдем определители
![]() ,
,
![]() и
и
![]() подставляя
столбец свободных членов
подставляя
столбец свободных членов
![]() вместо первого, второго и третьего
столбцов определителя
вместо первого, второго и третьего
столбцов определителя
![]() соответственно:
соответственно:
 ,
,
 ,
,
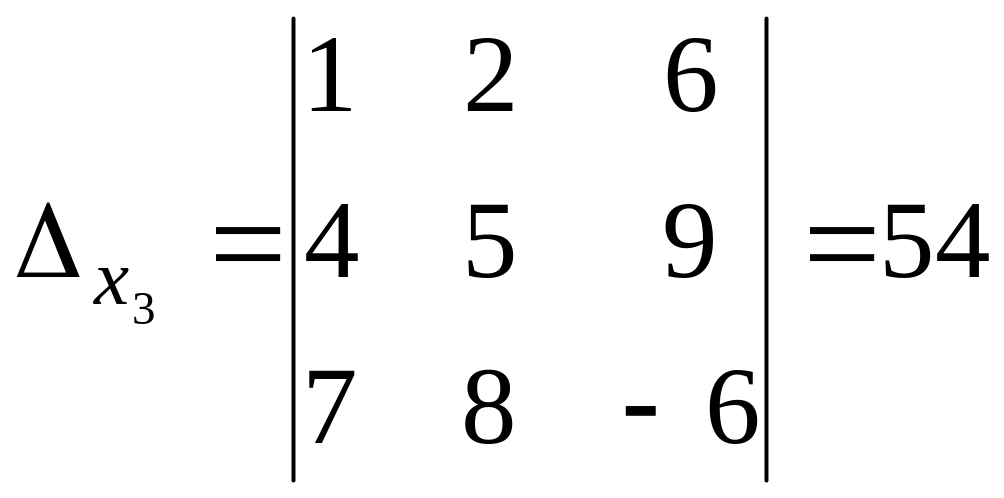 .
Отсюда получаем решение системы
уравнений:
.
Отсюда получаем решение системы
уравнений:
![]() ,
,
![]() ,
,
![]() .
.
2) Решим систему с
помощью обратной матрицы. Найдем матрицу
![]() ,
обратную к матрице системы
,
обратную к матрице системы
 .
.
Определитель
системы
![]() ,
то матрица
существует.
,
то матрица
существует.
Найдем алгебраические
дополнения ко всем элементам матрицы
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Запишем матрицу
 .
Найдем обратную матрицу
.
Найдем обратную матрицу
 .
Найдем решение системы
уравнений:
.
Найдем решение системы
уравнений:

 .
.
Итак,
![]() ,
,
![]() ,
,
![]() .
.
Пример 2 Исследовать систему линейных уравнений; если она совместна, то найти ее общее и одно частное решение.
![]()
Решение Приведем расширенную матрицу системы к ступенчатому виду:


Так как
![]() ,
то система совместна и неопределена.
,
то система совместна и неопределена.
Количество главных
переменных равно
![]() ,
количество свободных переменных равно
,
количество свободных переменных равно
![]() .
Выберем какой-нибудь отличный от нуля
минор второго порядка полученной матрицы
,
например, минор
.
Выберем какой-нибудь отличный от нуля
минор второго порядка полученной матрицы
,
например, минор
![]() .
Его столбцы – первый и второй столбцы
матрицы
– соответствуют переменным
.
Его столбцы – первый и второй столбцы
матрицы
– соответствуют переменным
![]() и
и
![]() – это будут главные
переменные, а
– это будут главные
переменные, а
![]() и
и
![]() – свободные переменные.
– свободные переменные.
Заметим, что в
качестве главных переменных в данном
примере нельзя выбрать пару
![]() и
,
т.к. любой соответствующий им минор
равен нулю:
и
,
т.к. любой соответствующий им минор
равен нулю:
![]() ,
,
![]() ,
,
![]() .
.
Запишем систему уравнений, соответствующую полученной расширенной матрице:
![]()
Перепишем ее в виде:
![]() или
или
![]()
Обозначим свободные
переменные:
через
![]() ,
через
,
через
![]() .
Запишем общее решение системы:
.
Запишем общее решение системы:
![]() ;
частное решение
;
частное решение
![]() .
.
Пример
3 Найти
площадь треугольника, образованного
двумя векторами
![]() и
и
![]() ,
исходящими из одной точки.
,
исходящими из одной точки.
Решение
Площадь треугольника, построенного на
векторах
![]() и
и
![]() ,
равна половине площади параллелограмма,
построенного на этих же векторах как
на сторонах, т.е. равна
,
равна половине площади параллелограмма,
построенного на этих же векторах как
на сторонах, т.е. равна
![]() модуля векторного произведения векторов
и
:
модуля векторного произведения векторов
и
:
![]() .
.
Векторное произведение найдем по формуле:
![]()
Найдем модуль полученного вектора, используя формулу:
![]()
Тогда
искомая площадь будет:
![]() (кв.ед.)
(кв.ед.)
Пример
4 Найти объем
пирамиды, построенной на трех некомпланарных
векторах:
![]() .
.
Решение
Объем пирамиды, построенной на трех
некомпланарных векторах как на ребрах,
равен
![]() ,
где
,
где
![]() ,
где
,
где
![]() –
смешанное произведение векторов.
–
смешанное произведение векторов.
Величину найдем по формуле:
=![]()
Тогда
![]() (куб.ед.).
(куб.ед.).
Пример
5 Написать
каноническое уравнение прямой, проходящей
через две точки
![]() и
и
![]() .
.
Решение
Уравнение прямой в пространстве,
проходящей через две точки
![]() и
и
![]() имеет
вид:
имеет
вид:
![]() .
В нашем случае получается:
.
В нашем случае получается:
![]() ;
;
![]() ;
;
![]() .
Это и есть каноническое уравнение прямой
в пространстве.
.
Это и есть каноническое уравнение прямой
в пространстве.
Пример
6 Написать
уравнение плоскости, проходящей через
три точки:
![]() ,
,
![]() и
и
![]()
Решение
Уравнение плоскости, проходящей через
три точки
,
и
![]() имеет вид:
имеет вид:
![]()
Подставив координаты заданных точек в это уравнение, получаем:
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
Пример
7 Написать
уравнение прямой, проходящей через
точку
![]() перпендикулярно плоскости
перпендикулярно плоскости
![]()
Решение
Каноническое уравнение прямой имеет
вид:
![]() .
Используя это уравнение получим:
.
Используя это уравнение получим:
![]() .
Проекции направляющего
вектора прямой
.
Проекции направляющего
вектора прямой
![]() найдем из условия перпендикулярности
прямой и плоскости. В нашем случае это
будет:
найдем из условия перпендикулярности
прямой и плоскости. В нашем случае это
будет:![]() ,
тогда будем иметь:
,
тогда будем иметь:![]() .
.
Пример 8 Дана
плоскость
![]() и вне ее точка
и вне ее точка
![]() .
Найти координаты точки
.
Найти координаты точки
![]() ,
симметричной точке
,
симметричной точке
![]() относительно
данной плоскости.
относительно
данной плоскости.
Решение Запишем уравнение любой прямой, проходящей через точку :
![]() .
Координаты
.
Координаты
![]() направляющего вектора прямой,
перпендикулярной плоскости, можно
заменить координатами нормального
вектора данной плоскости
направляющего вектора прямой,
перпендикулярной плоскости, можно
заменить координатами нормального
вектора данной плоскости
![]() .
Тогда уравнение этой прямой будет иметь
вид:
.
Тогда уравнение этой прямой будет иметь
вид:
![]() .
.
Найдем проекцию точки на данную плоскость, решив совместно уравнения
и
.
Представим каноническое уравнение
прямой в параметрическом виде:
 .
Подставляя эти выражения для
.
Подставляя эти выражения для
![]() ,
,
![]() и
и
![]() в уравнение плоскости, найдем
в уравнение плоскости, найдем
![]() ,
откуда
,
откуда
![]() ,
,
![]() ,
,
![]() .
.
Координаты
симметричной точки найдутся из формул
координат середины отрезка:
![]() ,
,
![]() ,
,
![]() .
Откуда
.
Откуда
![]() ,
,
![]() ,
,
![]()
