10. Ограниченность непрерывной функции на отрезке
Непрерывные функции, определенные на отрезке обладают определенными свойствами. Выполнения этих свойств не гарантируются, если область определения функции не является отрезок (то есть, когда область определения функции является интервал, полуинтервалы, полуоси и числовая ось).
Теорема 5. (Первая
теорема Вейерштрасса).
Пусть функция
определена и непрерывна на отрезке
.
Тогда она на этом отрезке ограничена и
снизу и сверху, то есть существуют такие
числа
и
,
что
для всех
.
11. Наибольшее и наименьшее значения непрерывной функции на отрезке
Пусть функция
определена на промежутке
.
Будем говорить, что число
является наибольшим
значением функции
на промежутке
,
если для любого
выполняется неравенство
.
Аналогичным образом определяется и
наименьшее значение. Будем говорить,
что число
является наименьшим
значением функции
на промежутке
,
если для любого
выполняется неравенство
.
Если область
определения функции является интервалом,
то функция может не достигать своего
наибольшего (наименьшего) значения.
Например, функция
определена и непрерывна на интервале
.
Наименьшее из чисел
,
для которых выполняется неравенство
,
является число
.
Однако ни при каких значениях
не выполняется равенство
.
Следовательно, функция
на интервале
не достигает своего наибольшего значения.
Наибольшее из чисел
,
для которых выполняется неравенство
,
является число
.
Однако ни при каких значениях
не выполняется равенство
.
Следовательно, функция
на интервале
не достигает своего наименьшего значения.
В рассмотренном
примере функция являлась непрерывной,
а область определения не являлась
отрезком. Рассмотрим теперь пример,
когда область определения функции
является отрезком, но сама функция не
является непрерывной. На отрезке
рассмотрим функцию
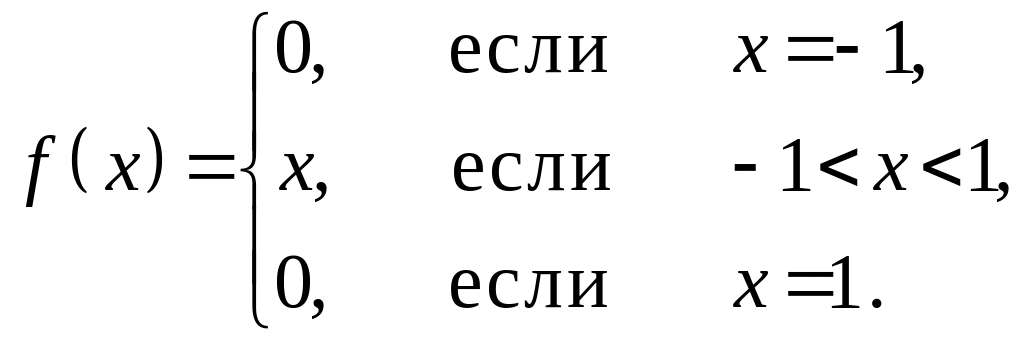
Наименьшее из
чисел
,
для которых выполняется неравенство
,
является число
.
Однако ни при каких значениях
не выполняется равенство
.
Следовательно, функция
на отрезке
не достигает своего наибольшего значения.
Наибольшее из чисел
,
для которых выполняется неравенство
,
является число
.
Однако ни при каких значениях
не выполняется равенство
.
Следовательно, функция
на отрезке
не достигает своего наименьшего значения.
Этот вопрос решается однозначно, если область определения функции является отрезком, а сама функция непрерывной.
Теорема 6. (Вторая
теорема Вейерштрасса).
Пусть функция
определена и непрерывна на отрезке
.
Тогда она на этом отрезке достигает
своего наибольшего и наименьшего
значения, то есть существуют такие
,
что
для всех
.
12. Равномерная непрерывность функции
Приведем определения непрерывности функции в точке и на промежутке.
Определение непрерывности функции на языке «-». Функция называется непрерывной в точке , если для любого найдется такое , что для всех удовлетворяющих условию выполняется неравенство :
.
Определение непрерывности функции на промежутке. Пусть функция определена в каждой точке промежутка . Функция называется непрерывной на промежутке , если она непрерывна в каждой точке этого промежутка:
.
Естественно, если промежуток содержит граничные точки, то в этих точках понимается односторонняя непрерывность.
Из приведенных
определений следует, что если функция
непрерывна в каждой точке промежутка
,
то даже для фиксированного
величины
будут различными для различных
.
Непрерывные функции, для которых величины
не зависят от
,
составляют важный класс непрерывных
функций.
Определение
равномерной непрерывности функции.
Функция
называется равномерно
непрерывной на промежутке
,
если для любого
найдется такое
,
что для всех
удовлетворяющих условию
выполняется неравенство
:
.
Теорема 7. (Теорема Кантора). Пусть функция определена и непрерывна на отрезке . Тогда она на этом отрезке является равномерно непрерывной.