2.4 Алгоритми на графах

Графи є зручними моделями при аналізі роботи і проектуванні комп’ютерних мереж.

Граф є кінцева множина V, яка називається множиною вершин, і множина Е двоелементних підмножин множини V. Множина Е носить назву множини ребер. Елемент множини Е називають ребром. Граф позначають G(V,E).

Зазвичай кінцевий граф, зображають у вигляді діаграми, на якій вершини це точки, а лінії – ребра.

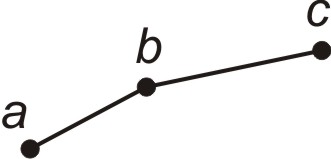
Якщо {a,b} – ребра, тоді вершини a і b називають їх кінцями. Ребро (a,b) називають інцедентним вершинам a і b. І, навпаки, вершини a і b інцедентні ребру (a,b). Дві вершини називають суміжними, якщо вони є кінцями ребра (інцедентні ребру). Два ребра називають суміжними, якщо вони інцедентні одній вершині (рис. 2.5)

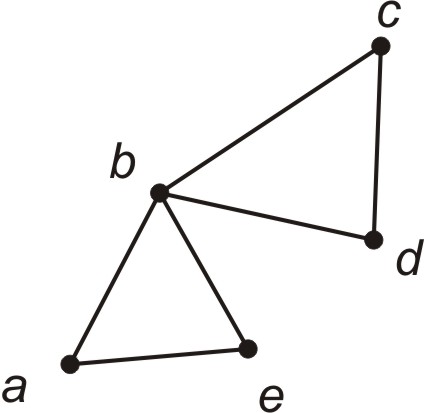
Рисунок 2.5 – Суміжні ребра (a,b) і (b,с)	Приклад. Граф з множиною вершин V={a,b,c,d,e} і множиною ребер E={(a,b), (a,e), (b,e), (b,c), (b,d), (c,d)} показаний на рис. 2.6
Визначені нами графи носять назву – простих. Обмеження на існування тільки одного ребра між двома вершинами дає можливість подати будь – яке ребро не як елемент множини Е.
	Рисунок 2.6 – Граф з множиною вершин V і множиною ребер Е.

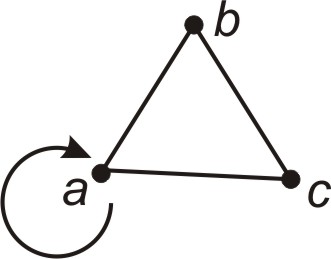
Наше визначення виключає також ребра, які називають петлями (рис. 2.7). Ребро яке з’єднує вершину саму з собою називається петлею. Граф, в якому є петлі, називають графом з петлями.

Рисунок 2.7 – Граф з петлею

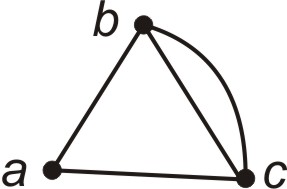
Якщо в графі є більше одного ребра між двома вершинами, то він носить назву мультиграфа (рис. 2.8) Рисунок 2.8 – Мультиграф.

Якщо граф має петлі і вершини, які з’єднані більше ніж одним ребром, то такий граф називають псевдографом

Степеню вершини , позначають deg(v), називають кількість ребер, які інцидентні даній вершині V. Вершина степені 0 називається ізольованою.

Граф, який складається із множини вершин V і множини Е упорядкованих пар елементів із V називається орієнтованим графом або орграфом. Ребра такого графа називають дугами. Якщо , то а – початкова, а b – кінцева вершини. Відмітимо, що поняття орграфа допускає наявність петель, чого не було у випадку простих графів. Це пояснюються тим, що орграф допускає відношення між елементами, а простий граф визначений як множина вершин і ребер, а в множині два однакових елементи вважаються одним елементом.

Якщо а – початкова, а b – кінцева вершини орграфа G(V,E), то вершини a і b інцидентні ребру (a,b); вершина а суміжна до вершини b, і, навпаки, вершина b також суміжна до вершини а.

Степеню виходу вершини називається кількість ребер, для яких є початковою вершиною, позначається outdeg( ). Степеню входу вершини називається кількість ребер, для яких є кінцевою вершиною і позначається . Якщо =0, то називається джерелом. Якщо outdeg( )=0, то вершина називається стоком (рис. 2.9).

Існує два способи подання граф як набір списків суміжних вершин або як матрицю суміжності.

Подання графа у вигляді списку суміжних вершин використовує масив із списків – по одному на кожну вершину ( - кількість вершин графа). Для кожної вершини список суміжних вершин вміщує у довільному порядку всі суміжні з нею вершини, для яких . На рис. 2.10,б показано подання неорієнтованого графа (рис.2.10,а) за допомогою списку суміжних вершин, а на рис 2.10,в той же граф поданий за допомогою матриці суміжності.

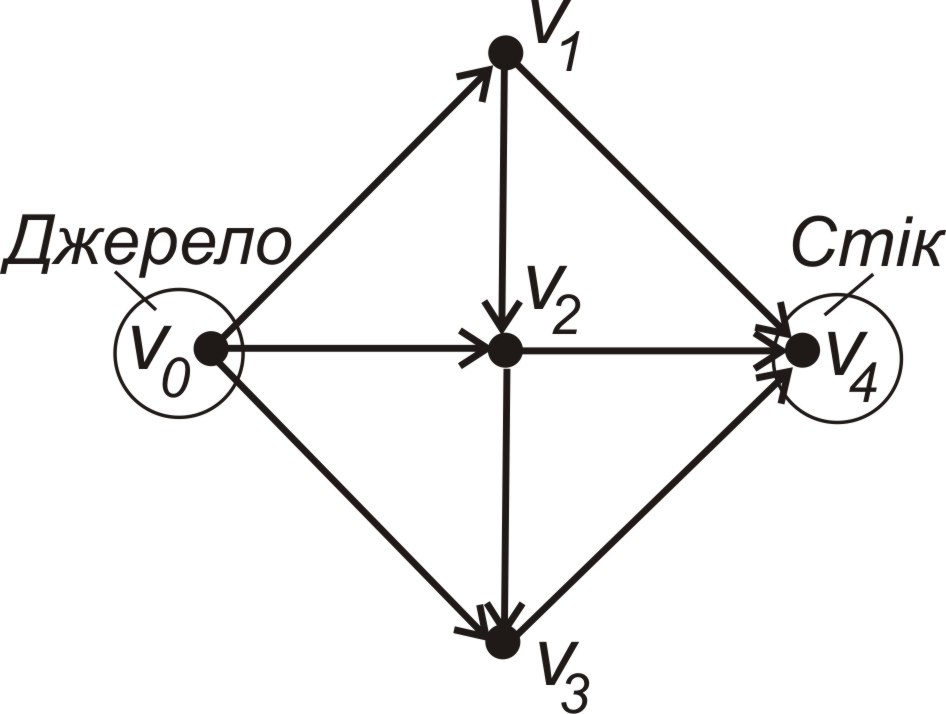
Рисунок 2.9 - Орграф, в якому є джерело і стік

а б в

Рисунок 2.10 – Два подання неорієнтованого графа

Аналогічним чином можна подати і орграф: у вигляді списку суміжних вершин (рис. 2.11,б) та у вигляді матриці суміжності (рис. 2.11,в).

Для орієнтованого графа сума всіх елементів матриці суміжності дорівнює числу його дуг (орієнтованих ребер), а для неорієнтованого графа – подвоєній сумі елементів матриці суміжності, так як ребро асоційовано в таблиці суміжності з двома елементами: як з вершиною , так і з вершиною . В обох випадках кількість пам’яті є . Списки суміжних вершин зручні для зберігання графів з вагами, в якому кожному ребру назначена певна вага (вагова функція). Недолік такого способу наступному: якщо необхідно дізнатись чи є у графа ребро із у , то необхідно проглянути увесь список у пошуку . Цього можна уникнути, подавши граф у вигляді матриці суміжності – але тоді буде потрібно більше пам’яті.

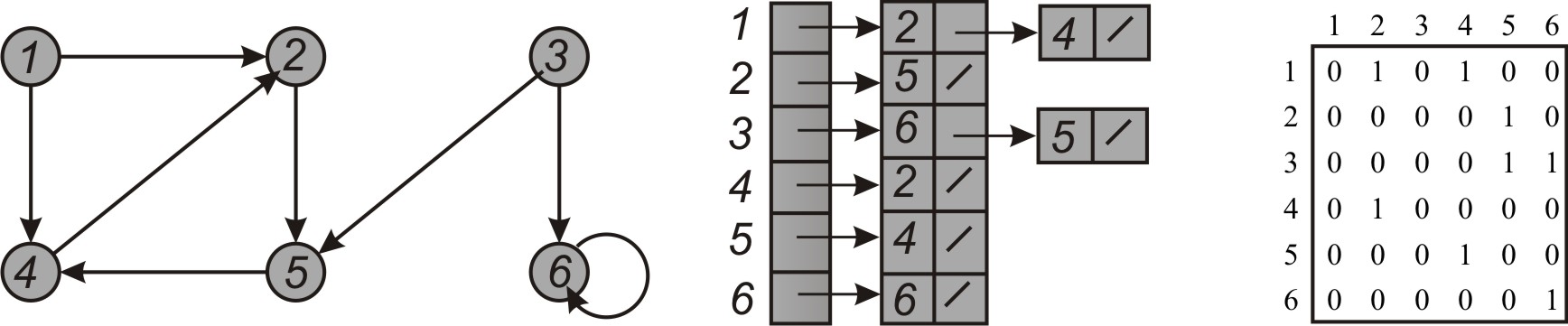
а б в

Рисунок 2.11 – Два подання орієнтованого графа

При використанні матриці суміжності будемо нумерувати вершини графа числами 1, 2, …, і розглядатимемо матрицю розміром , елементи якої

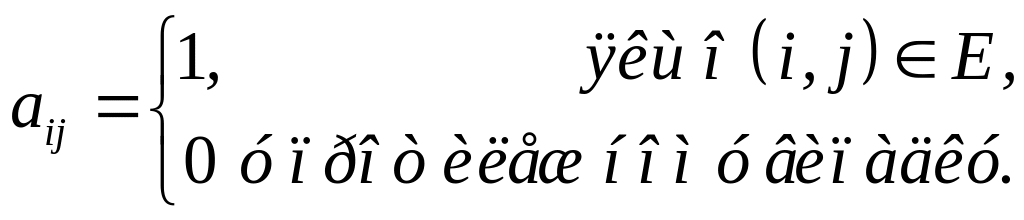
На рис. 2.10,б і 2.11,б наведені матриці суміжності для неорієнтованого і орієнтованого графів відповідною. Матриця суміжності вимагає пам’яті незалежно від кількості ребер.

Оскільки матриця суміжності неорієнтованого графа симетрично, то вона співпадає зі своєю транспонованою матрицею, тобто . Завдяки симетрії матриці у пам’яті машини можна зберігати лише числа на головній діагоналі і числа, які розміщені вище головної діагоналі. Зберігання ваг ребер графа у пам’яті машини здійснюється у матриці на пересіченні лінійки і стовпця.