
- •Оглавление
- •Введение
- •Матричная алгебра
- •Матрицы
- •Действия над матрицами
- •Определители
- •Свойства определителей
- •Обратная матрица
- •Системы линейных уравнений
- •Решение систем линейных уравнений
- •Модель Леонтьева многоотраслевой экономики
- •Задание для контрольной работы
- •Правила выполнения и оформления контрольных работ
- •Библиографический список
Обратная матрица
Матрица
![]() называется обратной
для квадратной матрицы
,
если
называется обратной
для квадратной матрицы
,
если ![]() .
.
Квадратная матрица имеет обратную тогда и только тогда, когда ее определитель не равен нулю. Такие матрицы называются невырожденными. Невырожденная матрица имеет единственную обратную
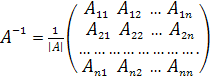 ,
,
где
![]() –
алгебраическое дополнение элемента
матрицы
.
–
алгебраическое дополнение элемента
матрицы
.
Пример
8.
Найти матрицу, обратную к матрице 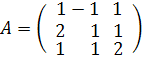 .
.
Решение. Вычислим определитель матрицы :
![]() .
Значит матрица
невырожденная и имеет обратную. Находим
.
Значит матрица
невырожденная и имеет обратную. Находим
 .
.
Для
проверки правильности вычислений
полезно убедиться, что для найденной
матрицы верно равенство ![]() .
.
Системы линейных уравнений
Решение систем линейных уравнений
Система линейных уравнений имеет вид
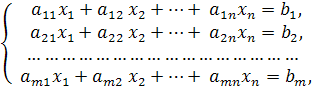
где
![]() –
коэффициенты при неизвестных,
–
коэффициенты при неизвестных, ![]() – свободные члены. Матрицы
– свободные члены. Матрицы
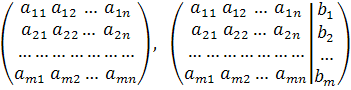
называют соответственно матрицей и расширенной матрицей системы.
Система уравнений называется совместной, если она имеет хотя бы одно решение. Совместная система имеет либо одно тогда она называется определенной, либо бесконечно много решений тогда – неопределенной. Система уравнений, не имеющая решений, называется несовместной.
Рассмотрим метод Гаусса решения системы линейных уравнений на конкретном примере.
Пример
9.
Решить систему 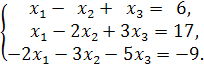
Решение.
Избавимся от переменной ![]() во втором и третьем уравнениях. Для
этого сначала домножим первое уравнение
на -1 и прибавим ко второму, а потом
домножим первое на 2 и прибавим к третьему.
во втором и третьем уравнениях. Для
этого сначала домножим первое уравнение
на -1 и прибавим ко второму, а потом
домножим первое на 2 и прибавим к третьему.
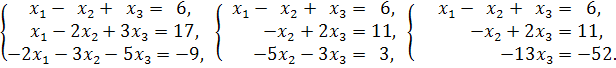
Отсюда
![]()
![]()
![]() .
.
Можно сделать те же преобразования с расширенной матрицей системы:
 .
.
Пример
10.
Решить систему 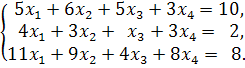
Решение.
Поменяем местами первую и вторую строки,
запишем расширенную матрицу системы.
Затем исключим переменную ![]() из второго и третьего уравнения.
из второго и третьего уравнения.
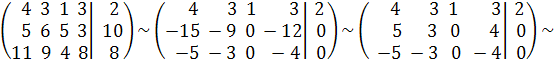
 .
.
Отсюда
![]()
![]()
![]() .
.
Положив
![]() и
и ![]() ,
получим
,
получим
![]() .
.
Пример
11. Обувная
фабрика специализируется по выпуску
изделий трех видов: сапог, кроссовок и
ботинок; при этом используется сырье
трех типов: ![]() ,
,
![]() ,
,
![]() .
Нормы расхода каждого из них на
изготовление одной пары обуви и объем
расхода сырья за один день заданы в
таблице.
.
Нормы расхода каждого из них на
изготовление одной пары обуви и объем
расхода сырья за один день заданы в
таблице.
Вид сырья |
Нормы расхода сырья на изготовление одной пары, усл.ед. |
Расход сырья за один день, усл.ед. |
||
сапог |
кроссовок |
ботинок |
||
|
5 2 3 |
3 1 2 |
4 1 2 |
2700 800 1600 |
Найти ежедневный объем выпуска каждого вида обуви.
Решение.
Пусть ежедневно фабрика выпускает ![]() пар сапог,
пар сапог, ![]() пар кроссовок и
пар кроссовок и ![]() пар ботинок. Тогда в соответствии с
расходом сырья каждого вида имеем
систему
пар ботинок. Тогда в соответствии с
расходом сырья каждого вида имеем
систему
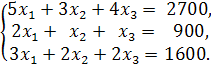
При решении системы методом Гаусса имеем
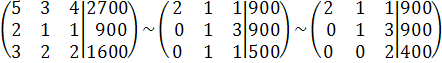 .
.
Отсюда
![]()
![]()
![]() .
.
Итак, фабрика выпускает 200 пар сапог, 300 пар кроссовок и 200 пар ботинок.
Модель Леонтьева многоотраслевой экономики
Пусть имеется отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, год). Введем следующие обозначения:
![]() – общий (валовой) объем продукции -ой
отрасли;
– общий (валовой) объем продукции -ой
отрасли;
– объем потребления -ой отраслью продукции -ой отрасли;
![]() – коэффициенты
прямых затрат,
показывающие затраты продукции -ой
отрасли на производство единицы
-ой
отрасли;
– коэффициенты
прямых затрат,
показывающие затраты продукции -ой
отрасли на производство единицы
-ой
отрасли;
![]() – объем конечного продукта -ой отрасли
для непроизводственного потребления.
– объем конечного продукта -ой отрасли
для непроизводственного потребления.
Так как валовой объем продукции -ой отрасли равен суммарному объему ее продукции, потребляемой всеми отраслями, и конечного продукта, то
|
(1) |
Уравнения (1) называются соотношениями баланса.
Основная задача межотраслевого баланса состоит в отыскании такого валового объема продукции для каждой из отраслей, который при известных прямых затратах обеспечивает заданный конечный продукт.
В матричной форме система (1) имеет вид
|
(2) |
Она
имеет ряд особенностей: прежде всего
все элементы матрицы
и компоненты
и ![]() должны быть неотрицательными.
должны быть неотрицательными.
Матрица , все элементы которой неотрицательны, называется продуктивной, если для любого с неотрицательными компонентами существует решение уравнения (2) – , все элементы которого неотрицательны. В таком случае и модель Леонтьева называется продуктивной.
Перепишем
систему в виде ![]() ,
откуда
,
откуда
|
(3) |
|
|
Матрица
![]() называется матрицей
полных затрат.
Каждый элемент
называется матрицей
полных затрат.
Каждый элемент ![]() матрицы
есть величина валового выпуска продукции
-ой отрасли, необходимого для обеспечения
выпуска единицы конечного продукта
-ой
отрасли.
матрицы
есть величина валового выпуска продукции
-ой отрасли, необходимого для обеспечения
выпуска единицы конечного продукта
-ой
отрасли.
Существует несколько критериев продуктивности матрицы . Приведем два из них.
Первый
критерий продуктивности.
Матрица
продуктивна тогда и только тогда, когда
матрица ![]() существует и ее элементы неотрицательны.
существует и ее элементы неотрицательны.
Второй
критерий продуктивности.
Матрица
с неотрицательными элементами продуктивна,
если сумма элементов по любому ее столбцу
(строке) не превосходит единицы: ![]() ,
причем хотя бы для одного столбца
(строки) эта сумма строго меньше единицы.
,
причем хотя бы для одного столбца
(строки) эта сумма строго меньше единицы.
Наряду с валовой и конечной продукциями в межотраслевом балансе рассматривается чистая продукция отрасли – разность между валовой продукцией этой отрасли и продукцией всех отраслей на производство этой отрасли.
Пример 12. В таблице приведены данные об исполнении баланса за отчетный период, ден.ед.
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
Валовой выпуск |
|
Энергетика |
Машиностроение |
|||
Энергетика Машиностроение |
7 12 |
21 15 |
72 123 |
100 150 |
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроения сохранится на прежнем уровне. Найти чистую прибыль отраслей.
Решение.
Имеем ![]() =100,
=100,
![]() =150,
=150,
![]() =7,
=7,
![]() =21,
=21,
![]() =12,
=12,
![]() =15;
=15;
![]() =72,
=72,
![]() =123.
=123.
Находим
коэффициенты прямых затрат: ![]() =0,07,
=0,07,
![]() =0,14,
=0,14,
![]() =0,12,
=0,12,
![]() =0,10,
т.е. матрица прямых затрат
=0,10,
т.е. матрица прямых затрат ![]() имеет неотрицательные элементы и
удовлетворяет критерию продуктивности:
имеет неотрицательные элементы и
удовлетворяет критерию продуктивности:
![]() .
.
Поэтому для любого конечного продукта можно найти необходимый объем валового выпуска по формуле (3).
Найдем
матрицу полных затрат
:
![]() .
Так как
.
Так как ![]() ,
,
![]() .
.
По
условию ![]() ,
тогда по формуле (1) получаем валового
выпуска
,
тогда по формуле (1) получаем валового
выпуска
![]() ,
,
т.е. валовой выпуск в энергетической отрасли надо увеличить до 179,0 ден.ед., а в машиностроительной – до 160,5 ден.ед.
Из
=179
ден.ед. валовой продукции энергетики
на внутрипроизводственное потребление
двух рассматриваемых отраслей (энергетики
и машиностроения) уйдет соответственно
![]() ден.ед. и
ден.ед. и ![]() ден.ед., так что чистая продукция
энергетики составит
ден.ед., так что чистая продукция
энергетики составит ![]() ден.ед. Аналогично, из
=160,5
ден.ед. валовой продукции машиностроения
на внутрипроизводственное потребление
уйдет соответственно
ден.ед. Аналогично, из
=160,5
ден.ед. валовой продукции машиностроения
на внутрипроизводственное потребление
уйдет соответственно ![]() ден.ед. и
ден.ед. и ![]() ден.ед., так что чистая продукция
машиностроения составит
ден.ед., так что чистая продукция
машиностроения составит ![]() ден.ед.
ден.ед.
