§ 4.2. Задача об остановке произвольной машины Тьюринга при произвольном входном слове

Т.1.5.(1) Теорема

Задача об остановке произвольной машины Тьюринга на произвольном входном слове алгоритмически неразрешима.

Иными словами, нельзя придумать универсальный алгоритм, в результате выполнения которого будет получен однозначный ответ: “да”- если произвольная машина Т остановится на ленте с произвольным входным словом t и “нет” – если Т не остановится на ленте t.

Доказательство

Докажем теорему от противного. Предположим, что задача об остановке произвольной машины Т при обработке произвольного слова t алгоритмически разрешима. Это означает, что существует алгоритм решения, а значит и существует реализующая его машина Тьюринга Д.

Построим машину Д, на ленте которой записано кодовое описание машины Т и кодовое описание входного слова t (рис.1.7).

кодовое описание машины Т

кодовое описание входного слова t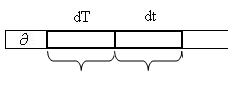

Рис. 1.7. Начальное состояние ленты машины Д.

Д обрабатывает эти два слова и пишет “да”, если Т останавливается при обработке t, и “нет“ если этого не происходит. Если этот алгоритм работает для любого случая (любого входного слова t), то должен работать и для частного случая. В качестве начального слова, в том числе, можно выбрать описание машины, т.е. возьмем dt = dT.

Построим машину Е, которая будет на своей ленте иметь описание произвольной машины Т. Работа машины Е состоит в том, что она копирует описание dT , а затем работает как Д. Если существует Д, то существует Е.

Построим машину F. F работает как E, но отличие состоит в том, что, если после работы на входном слове dT машина Е останавливается с ответом “да” (что означает что машина Т останавливается), то машина F не останавливается, а продолжает бесконечное движение вправо без изменения знаков на ленте. Если же вдруг машина Е останавливается с ответом «нет» (это означает, что машина Т не останавливается), то F просто останавливается.

Если данный алгоритм работает для произвольной машины Т, то и для конкретной тоже будет работать. Положим Т=F. Таким образом, на ленте машины F оказывается описание самой машины F. В результате получим, что машина F анализирует саму себя (F – самоанализирующая машина).

Получаем, что F не останавливается в том случае, если Е остановится с ответом “да”, а это означает, что машина Т остановится. Поскольку Т=F, имеем ситуацию: F остановится, если F не остановится, и F не остановится, если F остановится, что явно противоречит здравому смыслу. Такой машины существовать не может.

Поскольку все рассуждения были логически обоснованы, полученное противоречие означает, что ошибка в изначальном предположении о существовании машины Д (в данном доказательстве используется прямой метод). Отсюда напрямую следует, что задача об остановке произвольной машины Т на произвольном слове t алгоритмически неразрешима, Q.E.D.

§ 4.3. Задача об остановке произвольной машины Тьюринга на пустой ленте

Если бы имелся алгоритм (а значит и соответствующая машина Тьюринга) для решения проблемы остановки произвольной машины при обработке произвольного слова, то эта машина могла бы решить и проблему остановки на пустой ленте как частный случай. Но неразрешимость проблемы остановки при анализе произвольного слова непосредственно не означает неразрешимости проблемы остановки на пустой ленте, потому как последняя задача может оказаться более простой, так как ее сфера применения явно уже.

Однако мы можем показать, что эти задачи эквиваленты, в том случае, если для каждой пары машина-лента (T-t) докажем наличие соответствующей машины M_Tt , работающей на чистой ленте.

Т.1.5.(2) Теорема

Задача об остановке произвольной машины Тьюринга на пустой ленте алгоритмически неразрешима.

Доказательство

Для каждой пары машина-лента (T-t) докажем наличие соответствующей задачи остановки на пустой ленте для некоторой другой машины, предположим M_Tt. Машина M_Tt строится непосредственно по описанию T и t, если диаграмму состояний Т дополнить последовательностью новых состояний.

Предположим, что для пары T, t в некоторый момент времени лента выглядит таким образом (рис.1.8):

∂ r₁ r₂ … r_m r_m+1 r_{m+2 …} r_n λ λ λ

Рис 1.8. Лента машины Т в выбранной момент времени.

Новая машина M_Tt начинает работу на пустой ленте и работает по следующей программе:

S₁ λ → r₁ R S₂

S₂ λ → r₂ R S₃

…

S_m λ → r_m R S_m+1

S_m+1 λ → x R S_m+2

S_m+2 λ → r_m+2 R S_m+3

_…

S_n λ → r_n L S_х

S_х r_n-1 → r_n-1 L S_х

S_х r_n-2 → r_n-2 L S_х

_…

S_х r_m+2 → r_m+2 L S_х

S_х х → r_m+1 L S₀

S₀ r_m → далее работа аналогично машине Т на ленте t,

где:

x – некоторая буква, в других случаях не встречающаяся на входной ленте t;

S_{1, …,} S_n, S_х – новые состояния машины M_Tt, которых не было в машине Т.

Т.о. машина M_Tt при запуске на пустой ленте эквивалента машине Т, работающей на ленте t, так как, по сути, машина M_Tt просто печатает копию ленты t на своей ленте, затем выбирает нужную позицию и после этого становится полностью идентичной машине Т. Значит M_Tt и Т - эквивалентные машины.

Предположим, что задача об остановке машины на чистой ленте алгоритмически разрешима, значит ее можно решить и применительно к машине M_Tt, начинающей работу на чистой ленте. Соответственно, такая задача решается и для машины Т на ленте t, что есть противоречие с доказанным в Теореме 1.5.(1) утверждением о том, что для произвольной машины Т задача остановки при обработке произвольного слова t алгоритмически неразрешима. Отсюда следует, что задача об остановке машины на чистой ленте алгоритмически неразрешима, Q.E.D.

В данном доказательстве используется косвенный метод, называемый методом сведения.

В п.1.5.1. была доказана неразрешимость проблемы останова для произвольных пар (Т, t). Только что показано, что каждой паре (Т, t) соответствует легко конструируемая машина M_Tt, которая останавливается на пустой ленте тогда и только тогда, когда имеет место останов пары (Т, t).

Способность решать частные проблемы останова (Т, пустая лента), которая включает все ситуации (M_Tt, пустая лента), предоставила бы возможность решить все проблемы останова для произвольных пар (Т, t). Можно сказать, что значительно более трудная проблема для пар (Т, t) свелась к значительно более простой проблеме для пар (Т, пустая лента).

Сводимость – достаточно тонкое и важное понятие в теории вычислимости. Оказывается, можно определить бесконечную иерархию проблем неразрешимости возрастающей сложности, ни одна из которых не сводится к предшествующей. Было даже показано, что существуют пары неразрешимых проблем, ни одна из которых не сводится к другой.