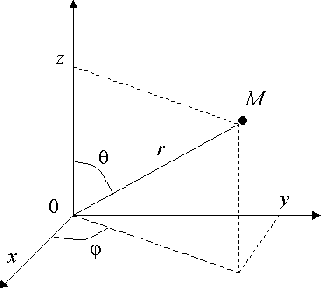
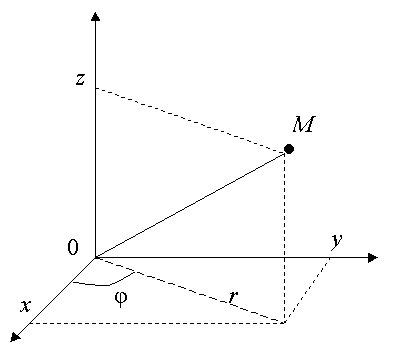
3.4.2. Преобразование координат в пространстве
Переход от декартовых
координат
к
цилиндрическим координатам
и
обратно:
; ; ; |
|
Переход от декартовых
координат
к
сферическим координатам
и
обратно:
,
|
|
,
;
Тема 4. Комплексные числа |
|
Мнимая единица
.
4.1. Алгебраическая форма комплексного числа
, где a, b – действительные числа;
a - действительная часть комплексного числа,
b - мнимая часть комплексного числа;
Обозначения действительной
и мнимой части:
.
Модуль комплексного
числа:
.
Сопряжённые комплексные
числа:
и
.
4.2. Действия над комплексными числами в алгебраической форме
;
;
.
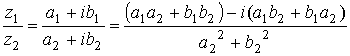4.3. Тригонометрическая форма комплексного числа
,
где
-
аргумент комплексного числа,
.
4.4. Показательная форма комплексного числа
.
Формула Эйлера:
.
4.5. Действия над комплексными числами в тригонометрической и показательной форме
,
,
,
где
.
Формула Муавра:
.
Тема 5. Введение в анализ |
|
5.1. Функции. Общие свойства
Числовая функция определена на множестве D действительных чисел, если каждому значению переменной поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
Аналитическое представление функции:
в явном виде:
;
в неявном виде:
;
в параметрической
форме:
;
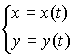разными формулами в
области определения (a,c]:
.
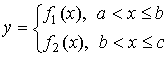Четная функция:
.
Нечетная функция:
.
Периодическая функция:
,
где T – период функции,
.
5.2. Основные элементарные функции
|
Название |
Формула |
Частные случаи |
1 |
Постоянная |
|
|
2 |
Степенная функция |
|
|
3 |
Показательная функция |
|
|
4 |
Логарифмическая функция |
|
|
5 |
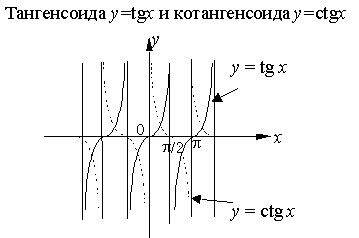
Тригонометрические функции |
|
|
6 |
Обратные тригонометрические функции |
|
|
;
;
;
;
;
;
;
;
.
;
;
;
Графики основных элементарных функций:
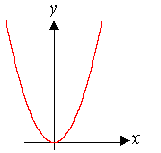
Парабола
|
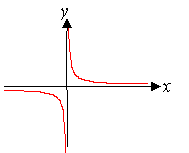
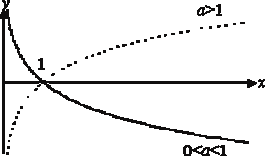
Гипербола
|
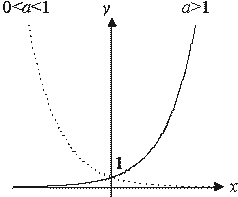
График показательной функции
|
График логарифмической фунгкции
|
Синусоида
|
|
|
|
и
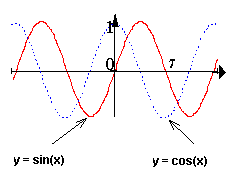
косинусоида
5.3. Теория пределов
Пределом функции
при
называется
число b, если для любого
(e
-сколь угодно малое положительное число)
можно найти такое значение аргумента
,
начиная с которого выполняется неравенство
.
Обозначение:
.
Пределом функции
при
называется
число b, если для любого
(e
-сколь угодно малое положительное число)
существует такое положительное число
d , что для всех значений x, удовлетворяющих
неравенству
выполняется
неравенство
.
Обозначение:
.
Формула для вычисления
предела элементарной функции
в
точке
,
где
:
.
Бесконечно малая
величина при
есть
функция
такая,
что
.
Бесконечно большая
величина при
есть
функция
такая,
что
.
Первый замечательный
предел:
.
Следствия:
;
;
Второй замечательный
предел:
,
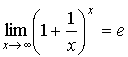где e=2,71828…
Следствия:
;
;
;
.
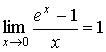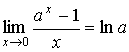Эквивалентные бесконечно
малые величины
при
:
x sinx tgx arcsinx arctgx ex-1 ln(1+x).
Виды неопределенностей:
Символическое обозначение |
Содержание неопределенности |
Пределы компонент при x a |
|
|
1(x) 0 2(x) 0 |
|
|
1(x) 2(x) |
|
|
(x) 0 (x) |
|
|
1(x) 2(x) |
|
|
(x) (x) |
|
|
1(x) 0 2(x) 0 |
|
|
(x) 0 (x) |
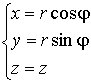
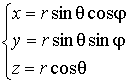
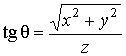