Яблонский Д1, Д6 вариант 20

Задание Д.1. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил

Камень скользит в течение τ с по участку АВ откоса, составляющему угол α с горизонтом и имеющему длину l. Его начальная скорость v_A. Коэффициент трения скольжения камня по откосу равен f. Имея в точке В скорость v_B, камень через Т с ударяется в точке С о вертикальную защитную стену. При решении задачи принять камень за материальную точку; сопротивление воздуха не учитывать.

Д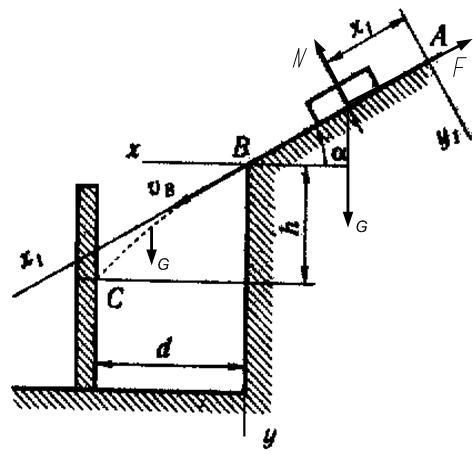ано:

α = 45°;

v_A = 0;

f = 0,3;

d = 2 м;

h = 4м;

Определить:

l - ?

τ - ?

Решение. Рассмотрим движение камня на участке АВ. Принимая камень за материальную точку, покажем действующие на него силы: вес , нор-мальную реакцию и силу трения скольжения . Составим дифференциаль-ное уравнение движения камня на участке АВ:

mx'' = ∑X_i1; mx₁'' = G∙sinα – F.

Сила трения

F = f∙N,

где

N = G∙cosα.

Таким образом,

mx₁'' = G∙sinα – f∙ G∙cosα

или

x₁'' = g∙sinα – f∙ g∙cosα.

Интегрируя дифференциальное уравнение дважды, получаем

x₁' = g∙(sinα – f∙cosα) ∙t + С₁;

x₁ = (g∙(sinα – f∙cosα)/2) ∙t² + С₁∙t + C₂;

Для определения постоянных интегрирования воспользуемся начальны-ми условиями задачи: при t = 0 х₁₀ = 0 и x₁' = 0.

Для t = 0: x₁' =С₁; х₁₀ =С₂.

Найдем постоянные: С₁ = 0, С₂ = 0.

Тогда

x₁' = g∙(sinα – f∙cosα) ∙t

x₁ = (g∙(sinα – f∙cosα)/2) ∙t²

Для момента τ, когда камень покидает участок,

x₁' = v_В ; x₁ = l,

т.е. l =(g∙(sinα – f∙cosα)/2) ∙ τ²;

v_В = g∙(sinα – f∙cosα) ∙ τ;

отсюда

τ = v_В/(g∙(sinα – f∙cosα));

Рассмотрим движение камня от точки В до точки С.

Показав силу тяжести , действующую на камень, составим дифферен-циальные уравнения его движения:

mx'' = 0; mу'' = G;

Начальные условия задачи: при t = 0

х₀ = 0; у₀ = 0;

x₀' = v_В ∙ cosα; у₀' = v_В ∙ sinα;

Интегрируем дифференциальные уравнения дважды:

x₀' =С₃; у₀' =С₄;

х₀ = С₅; у₀ = С₆.

Отсюда найдем, что

С₃ = v_В ∙ cosα; С₄ = v_В ∙ sinα;

С₅ = 0; С₆ = 0.

Получим следующие уравнения проекций скорости камня:

x' = v_В ∙ cosα, у' = g∙t + v_В ∙ sinα

и уравнения его движения:

x = v_В ∙ cosα ∙t, у = g∙t²/2 + v_В ∙ sinα∙t.

Уравнение траектории камня найдем, исключив параметр t из уравнений движения. Определив t из первого уравнения и подставив его значение во второе, получаем уравнение параболы:

у = g∙х²/(2 ∙ v_В² ∙ cos²α) + х∙ tgα.

В момент падения у = h, x = d.

Отсюда h = g∙ d ²/(2 ∙ v_В² ∙ cos²α) + d ∙ tgα.

Найдем v_В:

Зная v_В найдем τ и l:

τ = v_В/(g∙(sinα – f∙cosα));

τ = 4,43/(9,81∙(sin45 – 0,3∙cos45)) = 0,9 с;

l =(g∙(sinα – f∙cosα)/2) ∙ τ²;

l =(9,81∙(sin45 – 0,3∙cos45)/2) ∙ 0,9² = 2 м;

Задание Д.6. Применение основных теорем динамики к исследованию движения материальной точки

Ш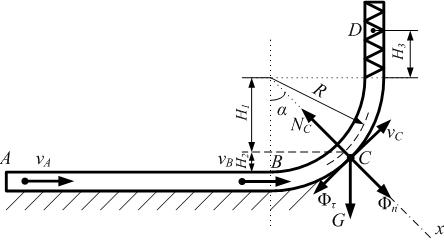арик, принимаемый за материальную точку, движется из положения А внутри трубки. Найти скорость шарика в положениях В и С, давление шари-ка на стенку трубки в положении С и максимальное сжатие пружины h.

Дано:

m = 0,2 кг

v_A = 10 м/с

τ = 1,0 с на АВ

R = 0,5 м

f = 0,1

α = 60°

h₀ = 0 см

с = 1,2 Н/см

v_B, v_C, N_C, h - ?

Скорость шарика в положении В найдем, применив на участке АВ теоре-му об изменении количества движения материальной точки:

Для определения v_C применим теорему об изменении кинетической энергии материальной точки:

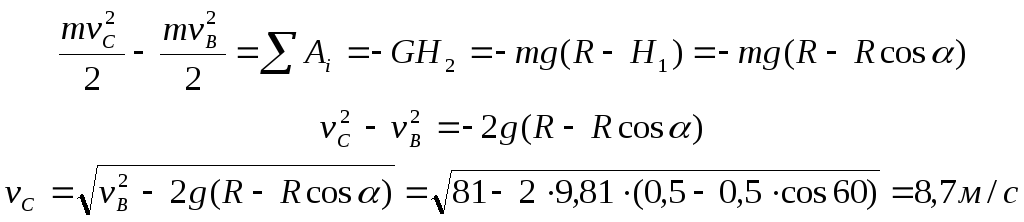
Определяем давление шарика на стенку канала в положении С.

В соответствии с принципом Даламбера для материальной точки геомет-рическая сумма сил, приложенных к точке, и силы инерции этой точки равна нулю:

Силу инерции материальной точки можно разложить на нормальную и касательную составляющие:

Сумма проекций сил на ось х должна быть равна нулю:

Отсюда

Для определения максимального сжатия h пружины воспользуемся на участке CD теоремой об изменении кинетической энергии материальной точки:

Учитывая, что v_D = 0 и H₃ = h, получаем

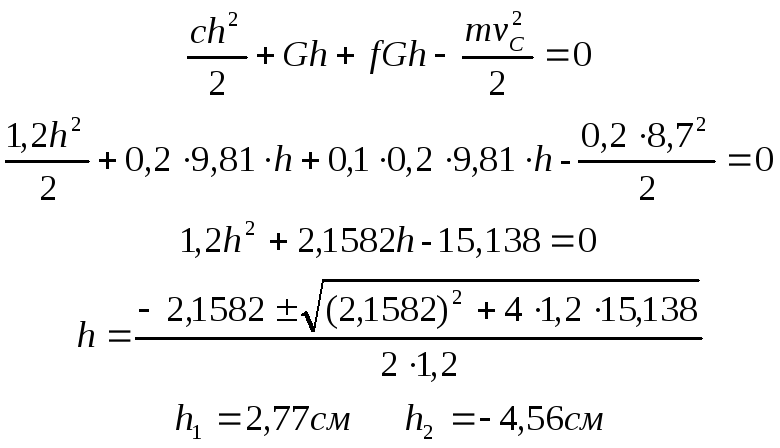
Принимаем в качестве искомой величины положительный корень квад-ратного уравнения:

h = 2,77 см = 0,0277 м

Ответ: v_B = 9 м/с, v_C = 8,7 м/с, N_C = 31,3 Н, h = 0,0277 м