
- •Семинар №1. Элементы векторного анализа.
- •§ 1.1. Основные теоретические сведения.
- •§ 1.2. Примеры решения типовых задач.
- •§ 1.3. Задачи для самостоятельного решения.
- •Литература
- •Семинар № 2. Уравнения Максвелла. § 2.1. Основные теоретические сведения.
- •§ 2.2. Примеры решения типовых задач.
- •§ 2.3. Задачи для самостоятельного решения.
- •Литература
- •Семинар № 3 Плоские электромагнитные волны. § 3.1. Основные теоретические сведения
- •§ 3.2.Примеры решения типовых задач.
- •§ 3.3. Задачи для самостоятельного решения
- •Литература
§ 1.2. Примеры решения типовых задач.
1.1. В декартовой системе координат проекции векторного поля А постоянны в каждой точке пространства:
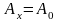 ,
,
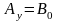 ,
,
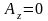 .
.
Построить картину силовых линий векторного поля.
Решение. Поскольку одна из декартовых составляющих векторного поля отсутствует, силовые линии должны представлять собой семейство плоских кривых, лежащих в плоскостях, параллельных плоскости ху. Вектор поля в каждой точке касателен к силовой линии, откуда вытекает дифференциальное уравнение силовых линий
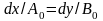 , (1.16)
, (1.16)
являющееся следствием подобия двух прямоугольных треугольников с катетами dх, dу и А0, В0соответственно. Общий интеграл уравнения (1.16) имеет вид
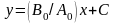 ,
,
где С - произвольная постоянная.
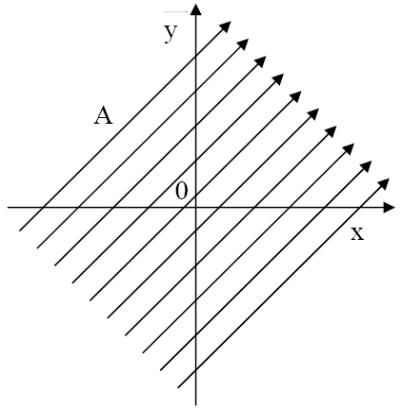
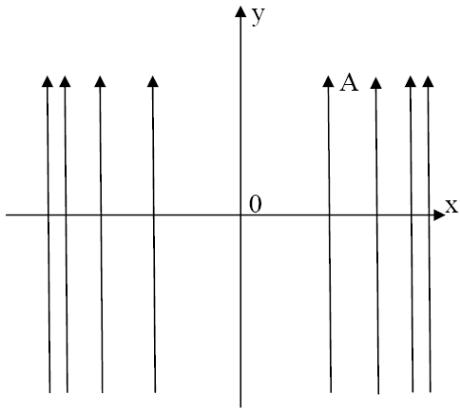
Рис.1.1 Рис.1.2
Таким образом, силовые линии поля представляют собой однопараметрическое семейство прямых с угловым коэффициентом наклона к оси х, равным В0 /А0 (рис. 1.1).
1.2. Векторное
поле А, удовлетворяющее во всех точках
рассматриваемой области условию
div А = 0,
называется соленоидальным (полем без
источников). При выполнении условия
rot А = 0
поле А является потенциальным векторным
полем. Если такое поле характеризует
силу, действующую на материальную точку,
то работа внешних сил при обходе
замкнутого контура будет равна нулю. В
декартовой системе координат векторное
поле А имеет единственную составляющую
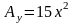 .
.
Проверить, является ли поле: а) соленоидальным; б) потенциальным.
Решение. Картина силовых линий поля А в плоскости ху изображена на рис. 1.2. Вычисляя дивергенцию этого поля по формуле (1.2), получим, что div А = ∂Аy/∂y = 0. Следовательно, исследуемое поле соленоидально. Однако в соответствии c (1.6) rot А = 30х1z, поэтому поле не является потенциальным.
1.3. Вычислить дивергенцию векторного произведения полей А и В. Решение. Здесь удобно воспользоваться оператором Гамильтона, записав
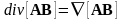 .
.
Оператор Гамильтона является дифференциальным оператором, поэтому к приведенному векторному произведению можно применит обычные правила дифференцирования произведения:
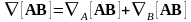 .
.
Нижние индексы у оператора указывают поле, на которое он воздействует. Поле, на которое оператор не воздействует, должно быть вынесено за знак оператора подобно константе. В результате получаем
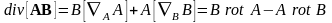 .
.
§ 1.3. Задачи для самостоятельного решения.
1.4. Скалярное поле φ задано в декартовой системе координат выражением
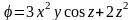
Вычислить векторное поле grad φ.
Ответ:
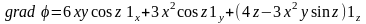 .
.
1.5. В декартовой системе координат векторное поле А имеет единственную составляющую Аz = 3у2. Построить качественно пространственную картину распределения силовых линий поля. Вычислить векторное поле rot А.
Ответ:
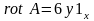 .
.
1.6. Пусть поле А предыдущей задачи характеризует векторы скоростей потока жидкости. В любую точку пространства может быть помещена миниатюрная “турбина” с прямыми лопатками (рис. 1.3); ориентация ее оси произвольна.
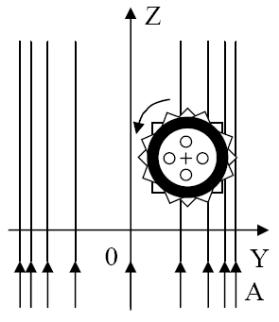
Рис.1.3.
Почему не
будет вращаться “турбина”, помещенная
в поток жидкости со скоростями, одинаковыми
в каждой точке? Почему угловая скорость
вращения равна нулю при
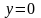 и изменяет направление при переходе из
области
и изменяет направление при переходе из
области
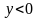 в область
в область
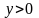 ?
Установить связь этих результатов с
математическим понятием ротора векторного
поля как циркуляции по бесконечно малому
контуру.
?
Установить связь этих результатов с
математическим понятием ротора векторного
поля как циркуляции по бесконечно малому
контуру.
1.7. В
сферической системе координат задано
векторное поле
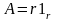 .
Определить скалярное поле div A.
Качественно построить картину силовых
линий векторного поля.
.
Определить скалярное поле div A.
Качественно построить картину силовых
линий векторного поля.
Ответ: div А = 3.
1.8. В
сферической системе координат векторное
поле А имеет единственную r-ю
составляющую, причем
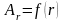 .
Какова должна быть функция
.
Какова должна быть функция
 ,
чтобы дивергенция поля А обращалась
тождественно в нуль? Построить картину
силовых линий поля.
,
чтобы дивергенция поля А обращалась
тождественно в нуль? Построить картину
силовых линий поля.
Ответ:
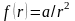 ,
где а - константа.
,
где а - константа.
1.9. В декартовой системе координат скалярное поле φ имеет вид
 ,
,
где
 мнимая единица;
мнимая единица;
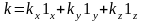 - постоянный вектор;
- постоянный вектор;
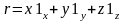 - радиус-вектор.
- радиус-вектор.
Найти выражения для grad φ и Δφ.
Ответ:
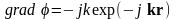 ,
,
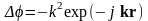 ,
где
,
где
 .
.
1.10. Определить
дивергенцию и ротор векторного поля,
имеющего в декартовой системе координат
единственную составляющую
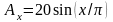 .
.
Ответ:
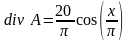 ,
,
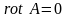 .
.
1.11.
Определить дивергенцию и ротор векторного
поля А, характеризуемого следующими
составляющими в цилиндрической системе
координат:
 ,
,
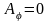 ,
.
,
.
Ответ:
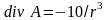 ,
.
,
.
1.13. В декартовой системе координат некоторое скалярное поле задано трехмерным интегралом Фурье
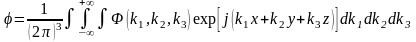
Вычислить Δφ.
Ответ:
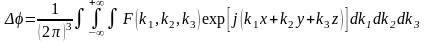 ,
где
,
где
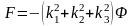 .
.
1.14. Изобразить графически картину силовых линий векторных полей, заданных в декартовой системе координат своими проекциями:
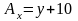 ,
,
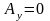 ,
.
,
.
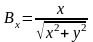 ,
,
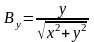 ,
,
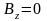 .
.
1.15. Найти ротор и дивергенцию следующих векторных полей, заданных в декартовой системе координат:
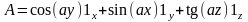 ,
,
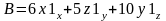 .
.
Ответ:
 ,
,
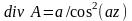 ,
,
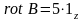 ,
,
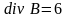 .
.
1.16. Используя правила действия с оператором Гамильтона, доказать тождество
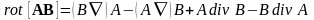 .
.
1.17. В
пространстве заданы два векторных поля
А и В. Найти выражение для поля
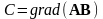 .
.
Указание: Выразить операцию grad через оператор и воспользоваться правилом дифференцирования произведения.
Ответ:
 .
.
1.18. Доказать следующие тождества векторного анализа (φ и А - произвольные дифференцируемые скалярное и векторное поля):
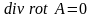 ,
,
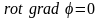 ,
,
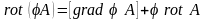 ,
,
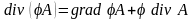 ,
,
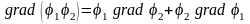 .
.
1.19. Векторное поле А обладает единственной составляющей Ax, которая постоянна в пределах плоского слоя толщиной 2d:
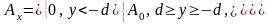
Найти выражение ротора поля.
Ответ:
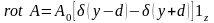 ,
где
,
где
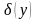 - функция Дирака.
- функция Дирака.
