1.Аналитическое решение дифференциальных уравнений.

Преобразуем каждое уравнение: перенесем неизвестные в левую часть уравнения, разделим каждое уравнение на коэффициент, стоящий перед второй производной (на массу m) и подставим численные значения: m = 60, k = 12.

1. Решаем уравнение (1).

Уравнение (1) является однородным дифференциальным уравнением второго порядка. Для его решения составим характеристическое уравнение

.

Корни этого уравнения:

r (r+0,2) = 0, откуда r₁ = 0, r₂ = - 0,2.

Корни характеристического уравнения – действительные, следовательно, решение уравнения (1) записывается в виде

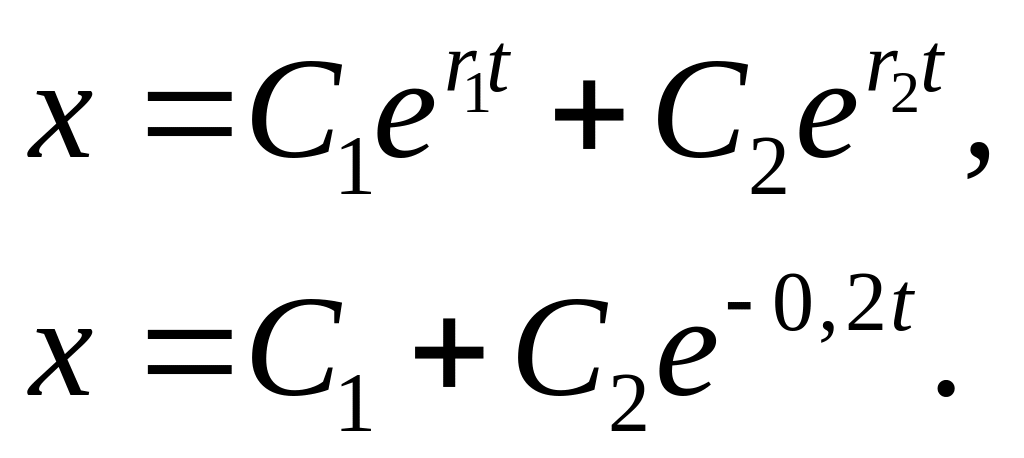(3)

С₁ и С₂ – постоянные интегрирования.

Определим С₁ и С₂. Для этого сначала находим

(4)

Уравнения (3) и (4) справедливы при любом значении t, следовательно, они справедливы при t = 0 . Подставим в уравнения (3) и (4) начальные условия:

Получим: 0 = С₁+ С₂, т.е. С₁ = - С₂.

16,74 = - 0,2 С₂,

откуда С₂ = - 83,7; С₁ = - С₂ =83,7.

Подставим значения С₁ и С₂ в уравнения (3) и (4), получим уравнение движения точки по оси х и проекцию скорости на ось х в зависимости от времени

(5)

2. Решаем уравнение (2)

(2)

Уравнение (2) является неоднородным дифференциальным уравнением второго порядка.

Решение этого уравнения равно

у = у₁ +у₂,

где у₁ –решение соответствующего однородного уравнения

, (3)

у₂ - частное решение уравнения (2).

Решаем однородное уравнение (3), записываем соответствующее ему характеристическое уравнение

,

где μ -корень этого характеристического уравнения, как и в первом случае, получаем

μ₁ = 0, μ₂ = - 0,2.

Тогда

Правая часть уравнения (2) – постоянное число, частное решение ищем в виде: , где А и В – коэффициенты, подлежащие определению. Подставим у₂ в уравнение (2), вычислив предварительно входящие в него первую и вторую производные по времени

, тогда .

Откуда А = - 49, В = 0 поскольку не входит в уравнение, тогда

у₂ = - 49,05 t.

Следовательно, полное решение уравнения (2) принимает вид

. (4)

Определяем постоянные интегрирования С₃ и С₄. Для этого сначала находим проекцию скорости на ось у

. (5)

Подставим в уравнения (4) и (5) начальные условия: t = 0, y₀ = 0,

V_y = 6,156

Откуда С₃ = - С₄, С₄ = - 276,03, С₃ = 276,03.

Тогда

Таким образом, движение точки описывается уравнениями

(6)

(7)

Проекции скорости на оси координат равны

(8)

(9) Полученные уравнения требуют наглядной геометрической интерпретации, поэтому необходимо построить по уравнениям (6) и (7) построить траекторию движения лыжника в воздухе. Строим график траектории движения точки в программе Mathcad.

Для построения траектории движения точки, представляющей собой график функции у = у(х), вызывается команда Plot, т.е. двумерный график в декартовой системе координат, находящийся в меню Graph. Строим траекторию (рис.4), соответствующую дифференциальным уравнениям (5) лыжника при его движении в воздухе в течение 4 секунд.

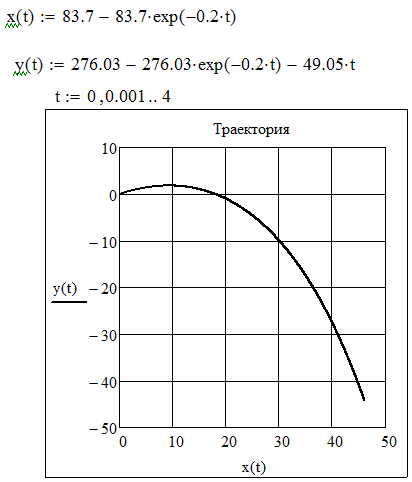
Рис . 4