4. Система линейных алгебраических уравнений

Определение 4.1.

Системой m линейных алгебраических уравнений с n неизвестными называют следующую систему уравнений первого порядка:

(24)

где

Матрица коэффициентов при неизвестных

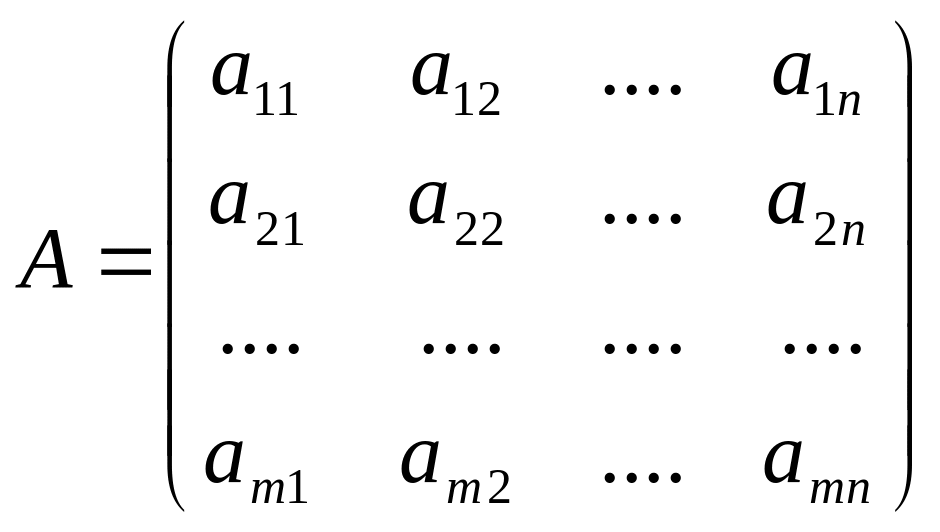
называется основной матрицей системы.

Матрица

называется расширенной матрицей системы.

Определение 4.2.

1). Множество всех значений , подстановка которых в систему уравнений 1.6 каждое уравнение обращает в тождество, называется решением данной системы.

2). Если все свободные члены системы равны нулю, то есть , то система называется однородной.

Определение 4.3.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной, если решение только одно, то система называется определенной, если решений множество, то система называется неопределенной. Если решений нет, то система несовместная.

Определение 4.4.

Две системы называются равносильными, если каждое решение первой системы является решением второй и наоборот.

Над системами можно производить следующие линейные преобразования:

1. менять уравнения местами;

2. умножать обе части уравнения на любое не равное нулю число;

3. прибавлять к обеим частям одного из уравнений системы соответствующие части другого уравнения, умноженное на любое действительное число.

4.1. Способы решения системы n линейных уравнений с n неизвестными. Матричный способ и метод Крамера

Пусть дана система n линейных уравнений с n неизвестными

(24’)

Назовем

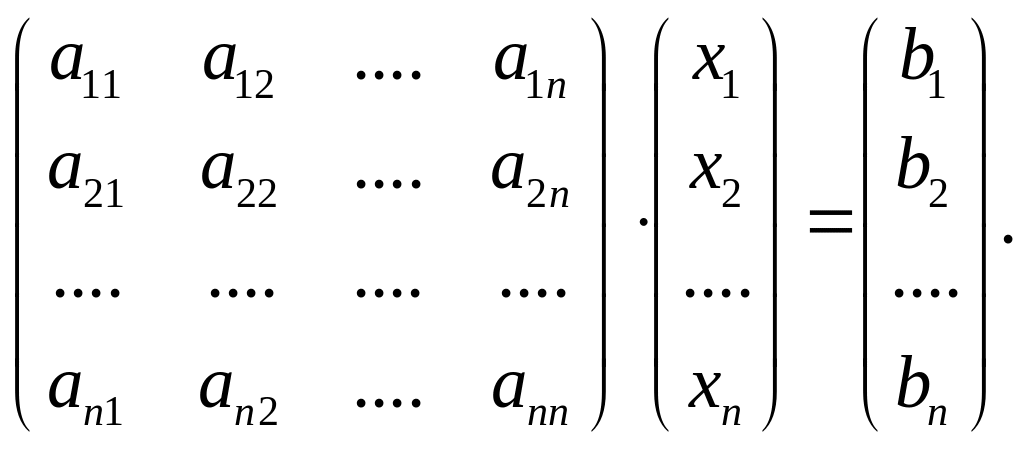(25)

матричным уравнением системы (24’)

или , (25’)

где .

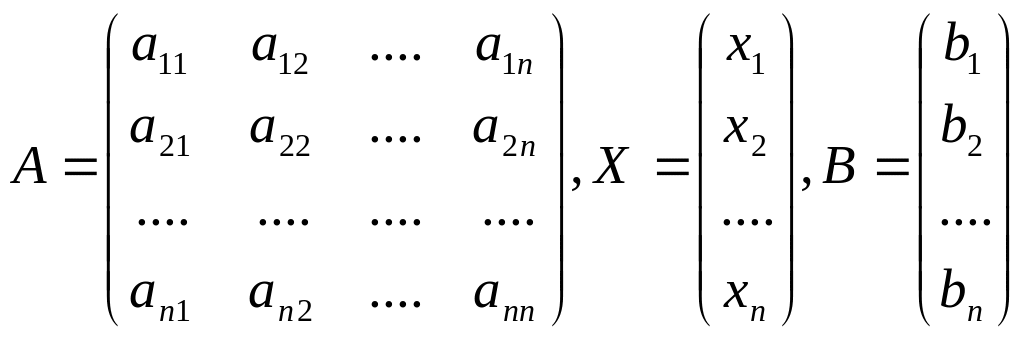Покажем, как найти решение системы (25’).

Каждую часть равенства (25’) умножим слева на обратную матрицу :

(26)

– решение системы (25’).

Запишем (26) в развернутом виде:

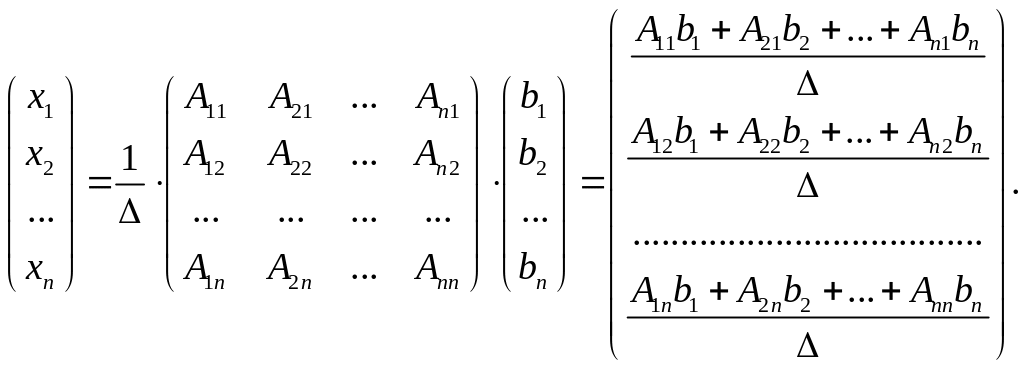
Таким образом, из определения равенства матриц следует:

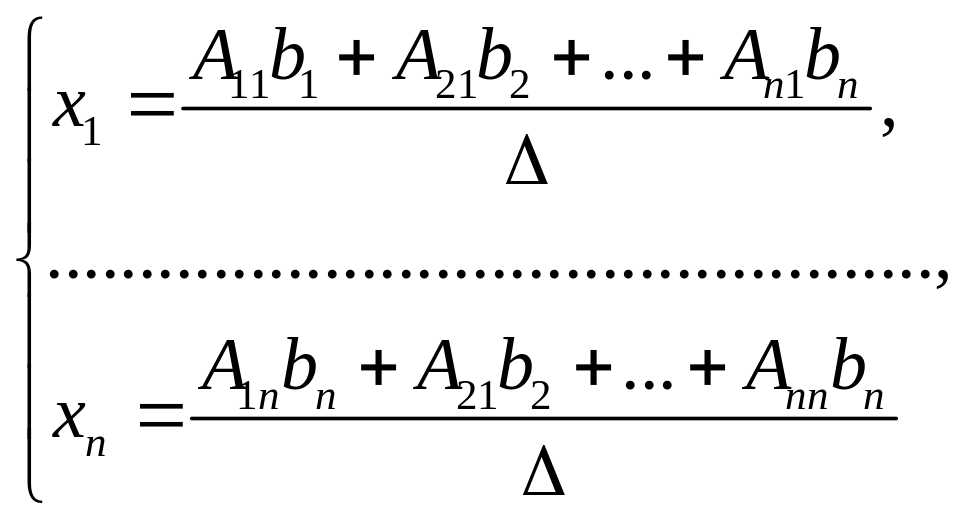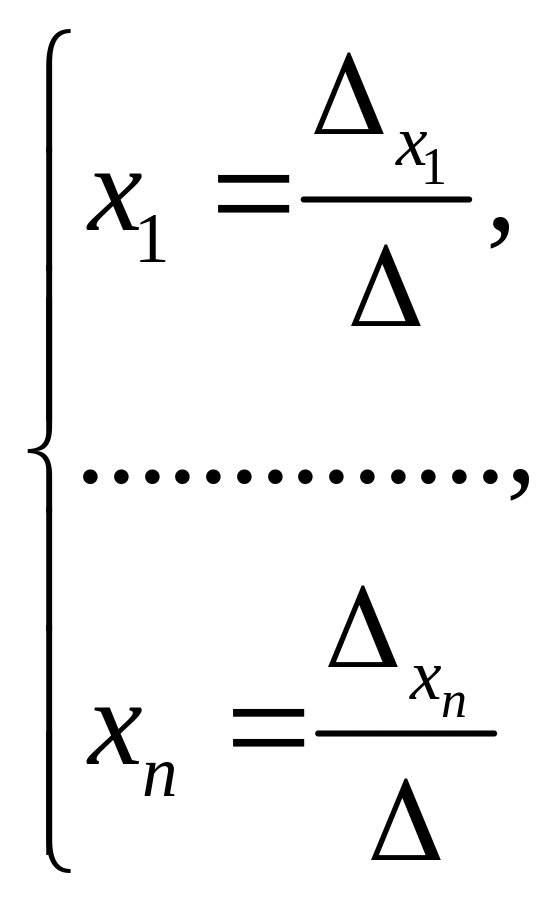или (27)

– формулы Крамера.

Пример 4.1.

Решить систему линейных алгебраических уравнений

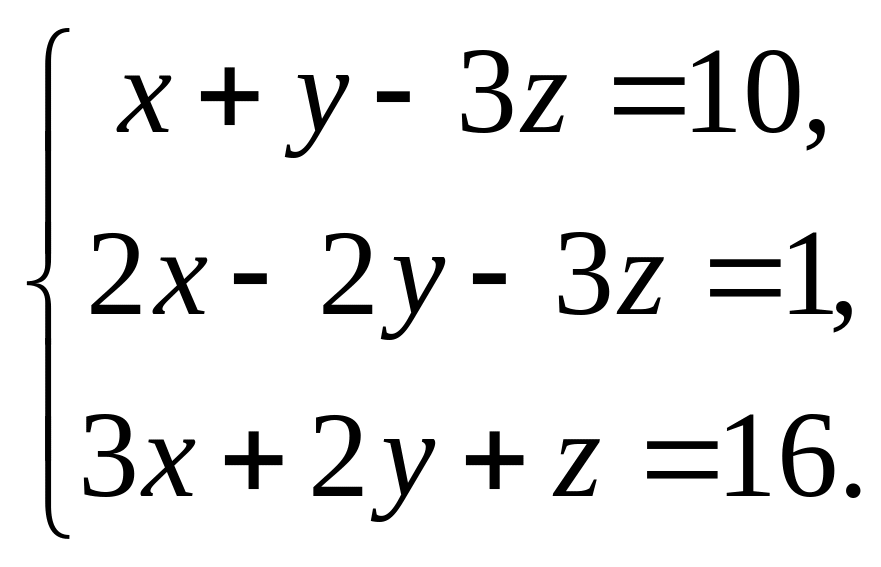
1) методом Крамера, 2) матричным способом.

Решение.

1. Метод Крамера

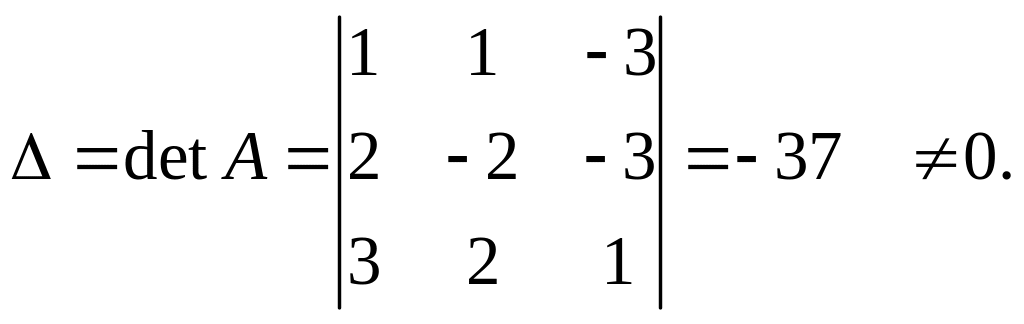
Следовательно, система имеет решение.

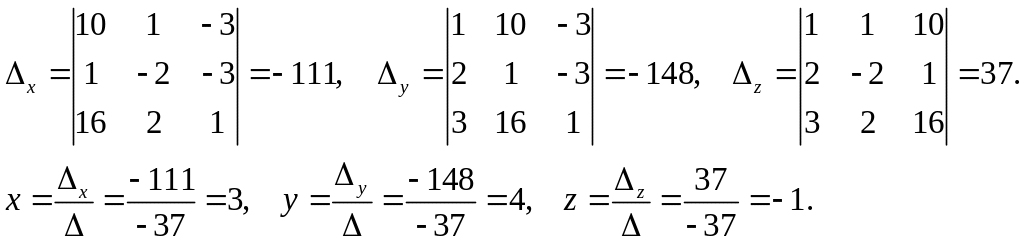
2) Матричный способ

Найдем обратную матрицу А^-1:

1 шаг:

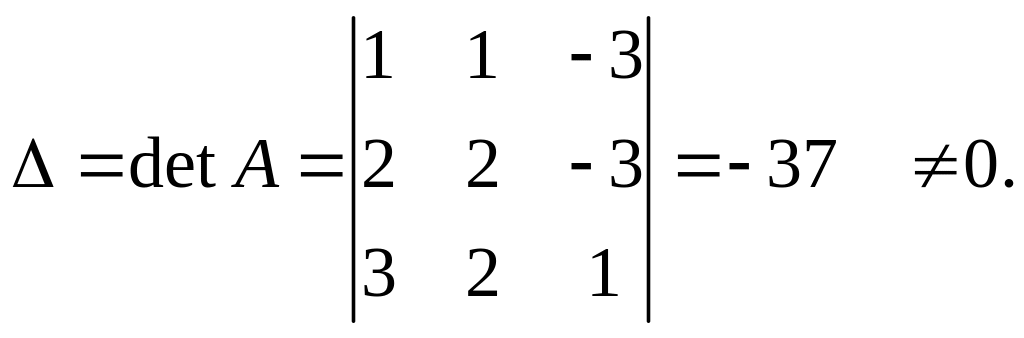
Следовательно, система имеет решение.

2 шаг:

ищем алгебраические дополнения

элементов матрицы .

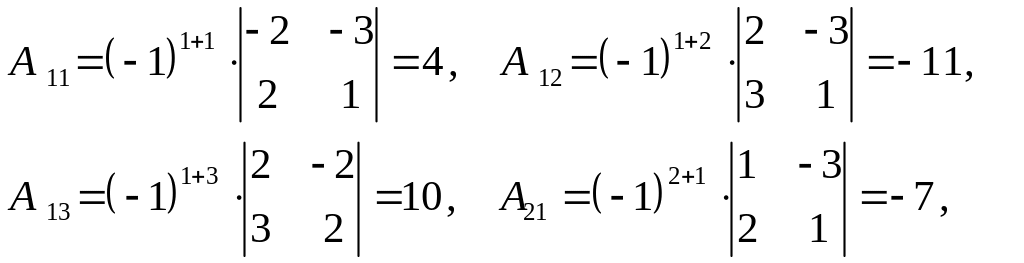
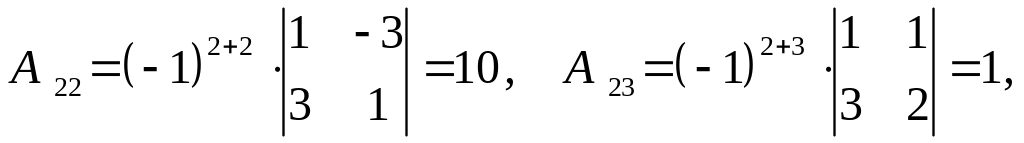
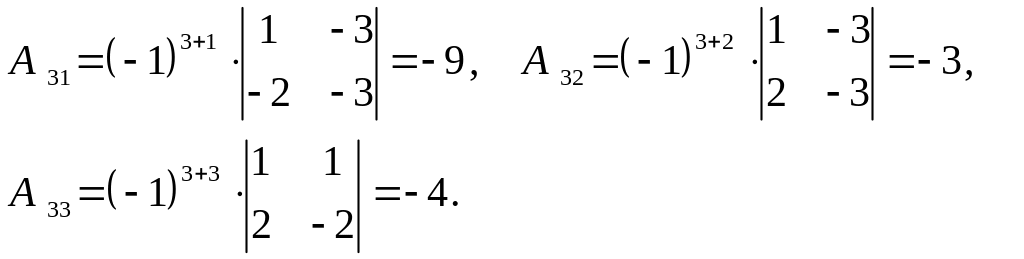
Составим матрицу из алгебраических дополнений

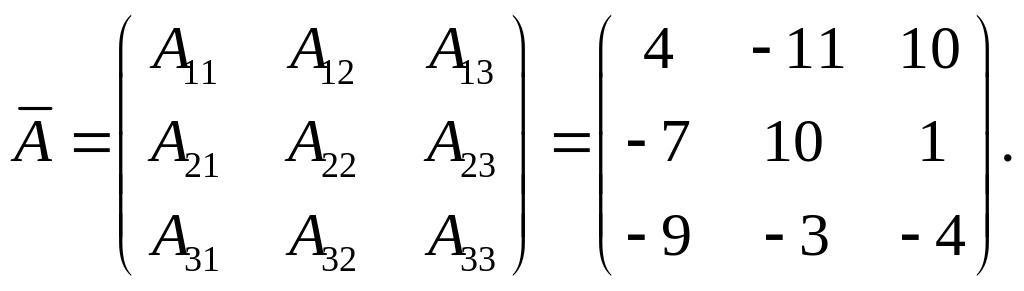
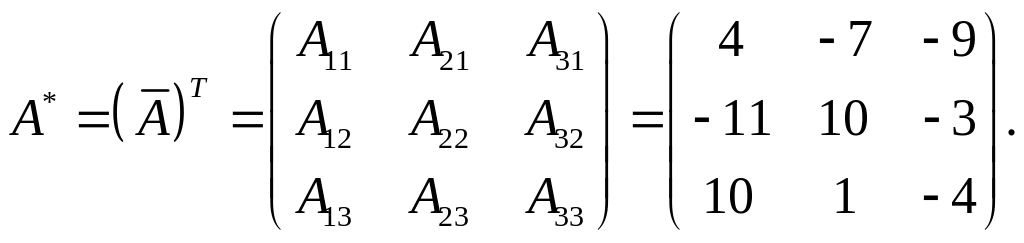
3 шаг: транспонируем матрицу

4 шаг:

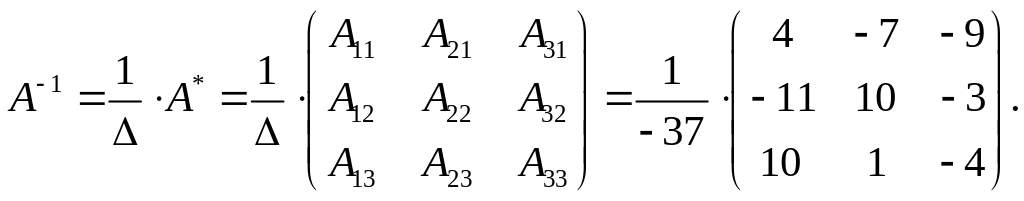
Получаем ответ:

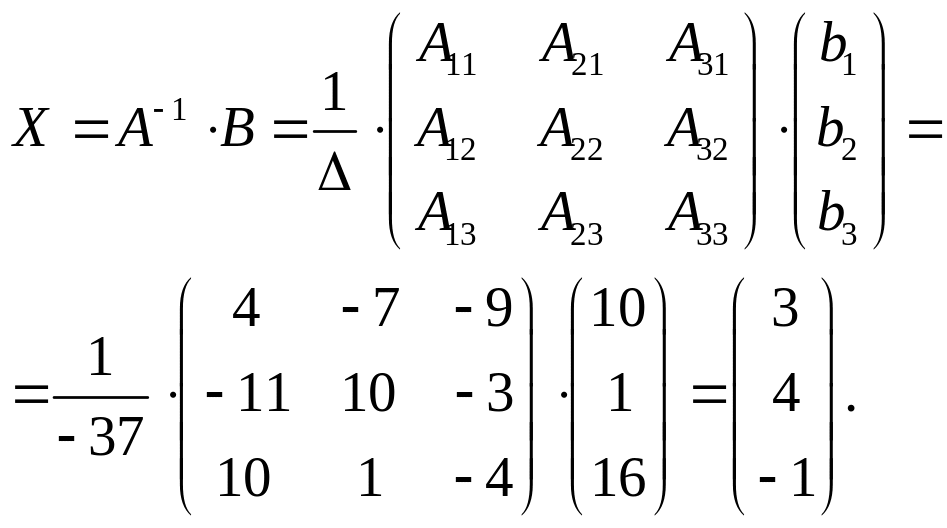
4.2. Способ решения системы m линейных уравнений с n неизвестными – метод Гаусса (метод последовательного исключения переменных)

На практике чаще всего применяется метод Гаусса – метод построения решения систем линейных уравнений.

Метод Гаусса состоит в следующем:

1. расширенную матрицу системы элементарными преобразованиями приводят к ступенчатому виду;

2. сравнивают ранги основной и расширенной матриц и делают вывод о совместности или несовместности системы;

3. в случае совместности системы в основной матрице выбирают базисный минор и дальнейшими элементарными преобразованиями строк добиваются того, чтобы в этом миноре все элементы вне главной диагонали стали равными нулю, а элементы главной диагонали стали равными единице;

4. выписывают систему, соответствующую полученной расширенной матрице, после чего переписывают систему, оставляя базисные неизвестные слева и переведя остальные слагаемые в правую часть;

5. если , то в правой части стоят только свободные члены и получено единственное решение;

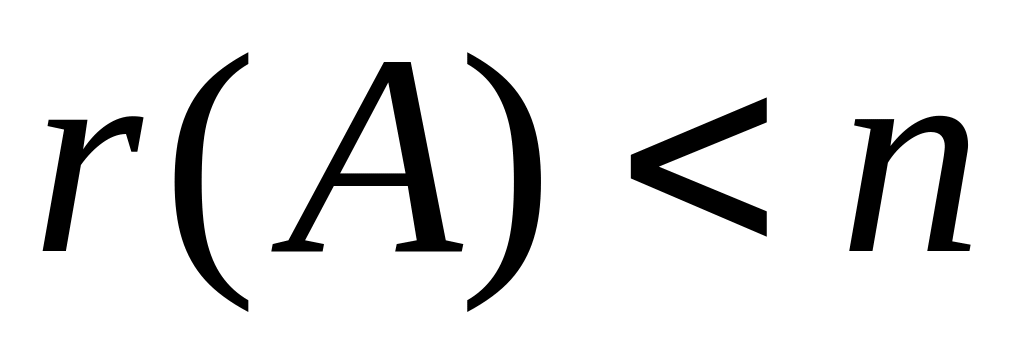6. если , то в правой части есть свободные неизвестные. Придавая им произвольные значения, получаем общее решение системы.

Пример 4.2. Решить следующую систему уравнений методом Гаусса:

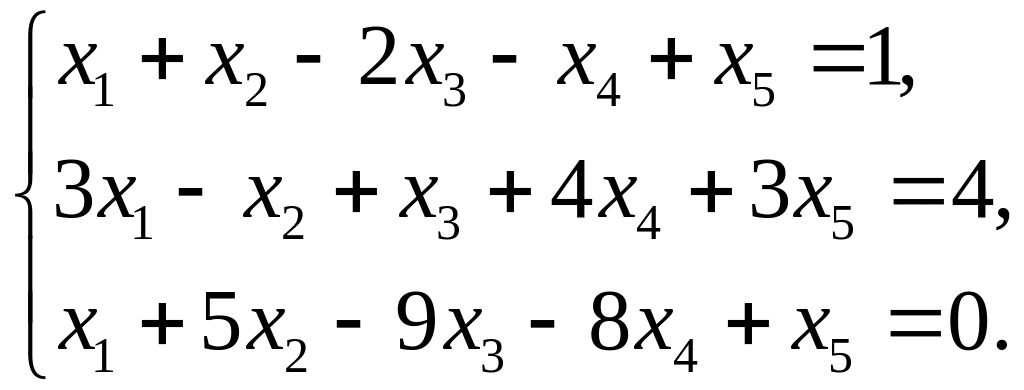
Решение.

 

 

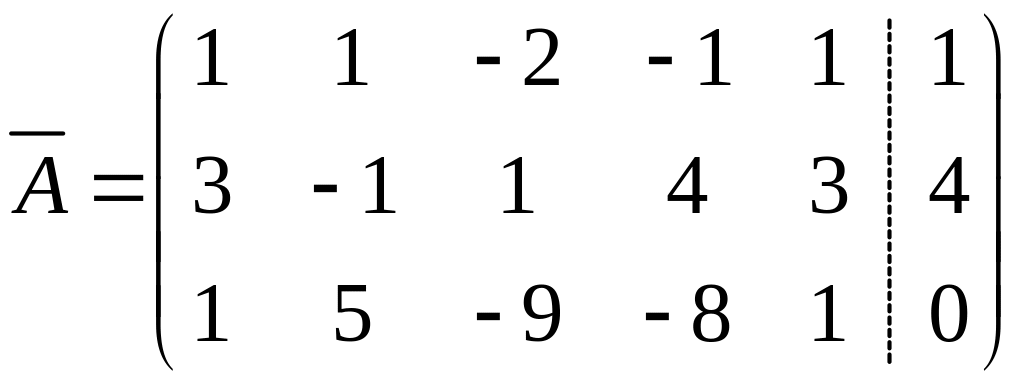
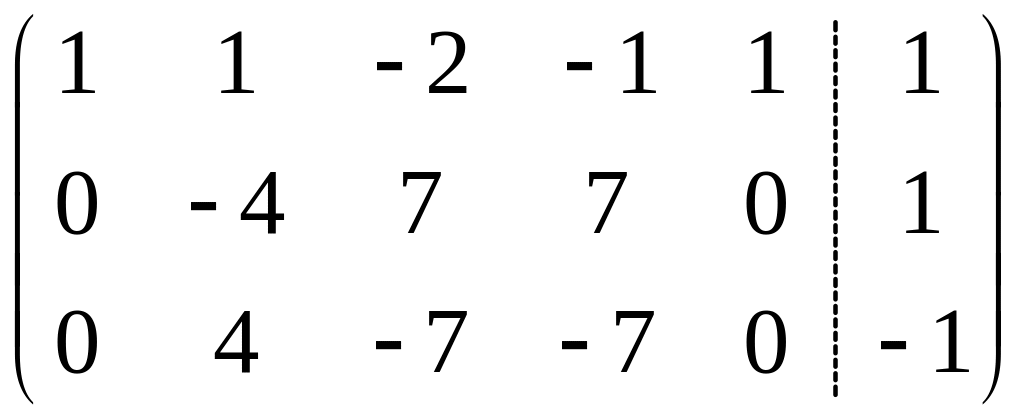
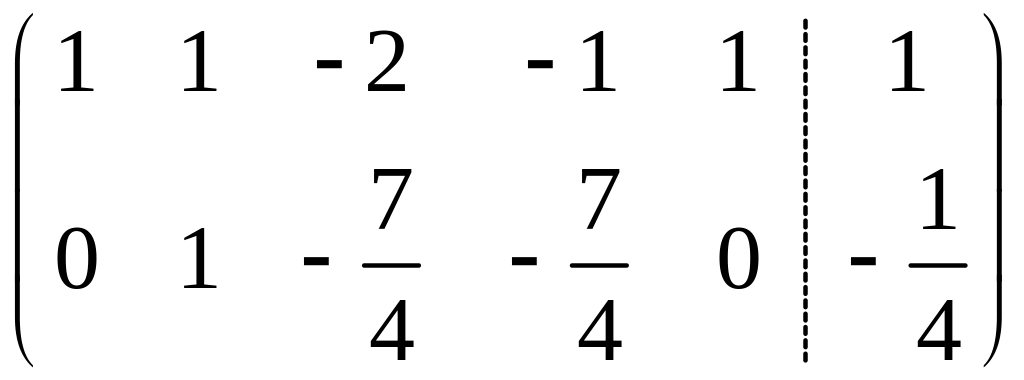
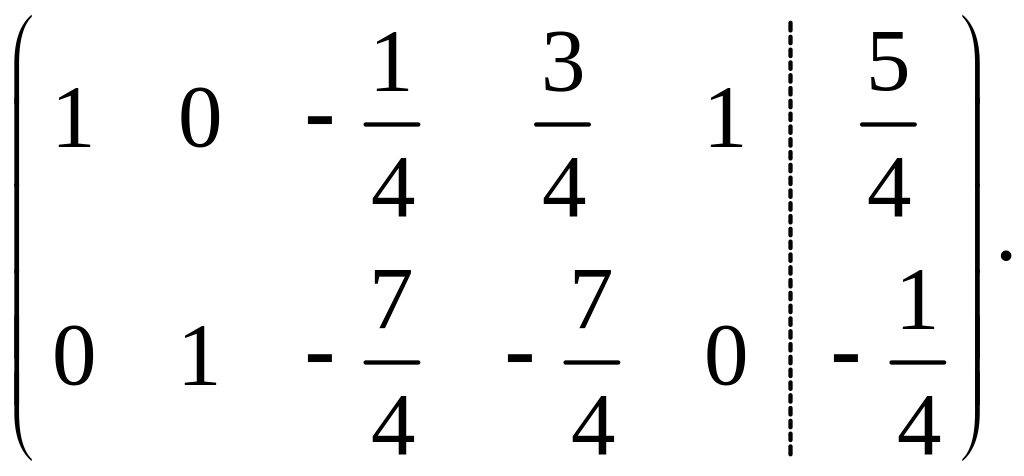
Таким образом,

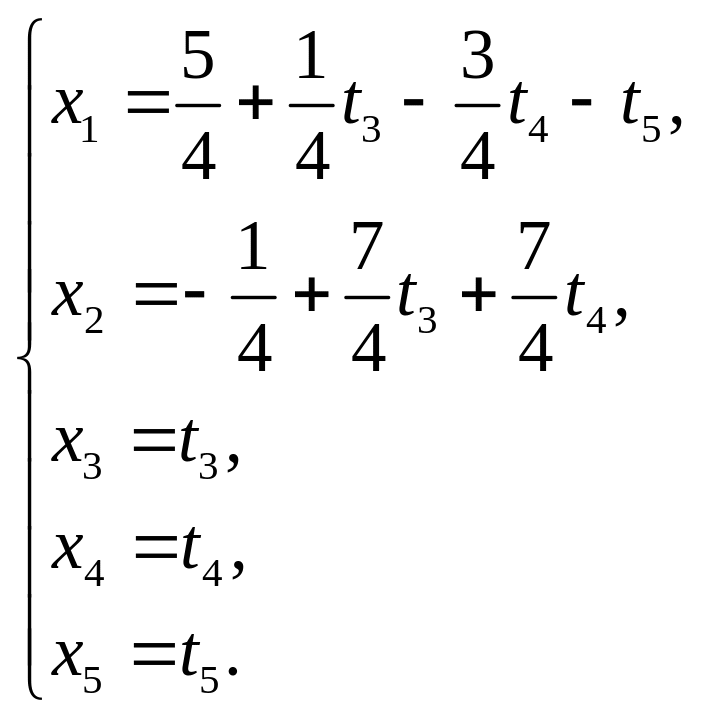
– общее решение или

( , , , ).

Пример 4.3. Решить следующую систему уравнений методом Гаусса:

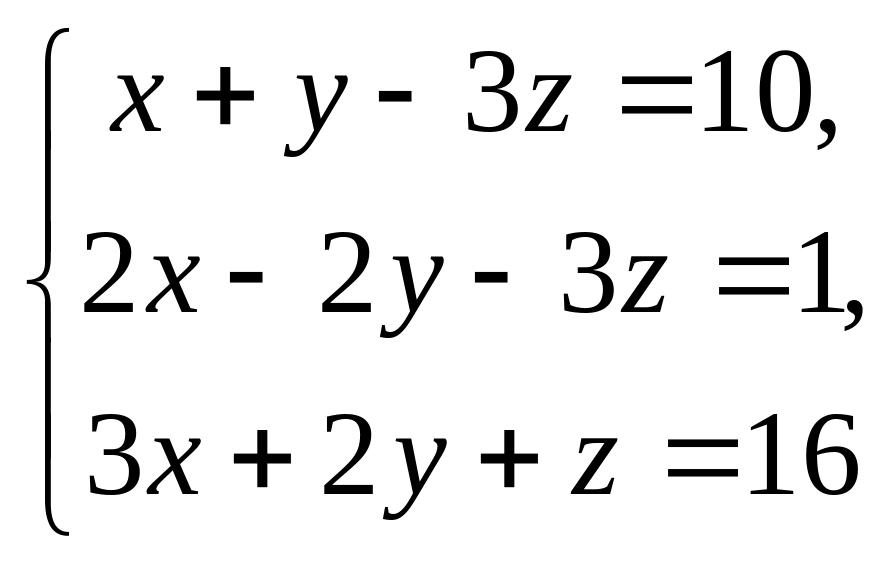
Решение.

Составляем расширенную матрицу (A|B), преобразуем ее так, чтобы вместо матрицы А получить единичную, тогда вместо матрицы B получим ответ.

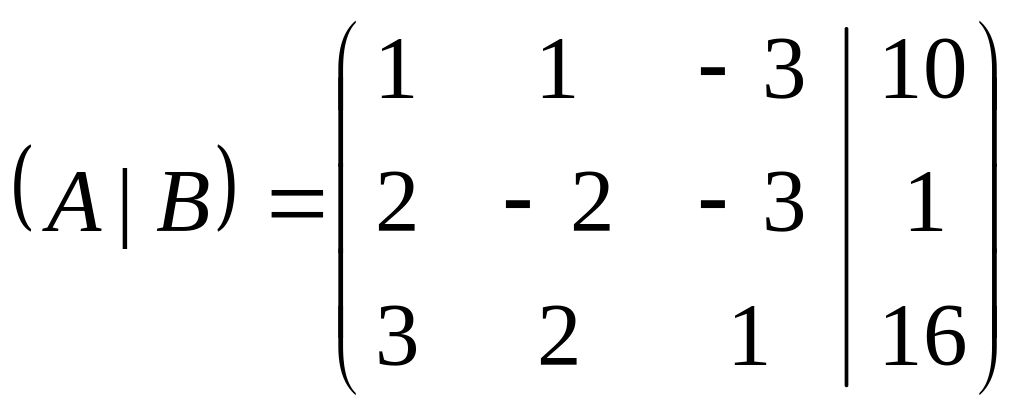~ 2^ая строка +1^ая, умноженная на -2; 3^ая строка +1^ая, умноженная на -3 ~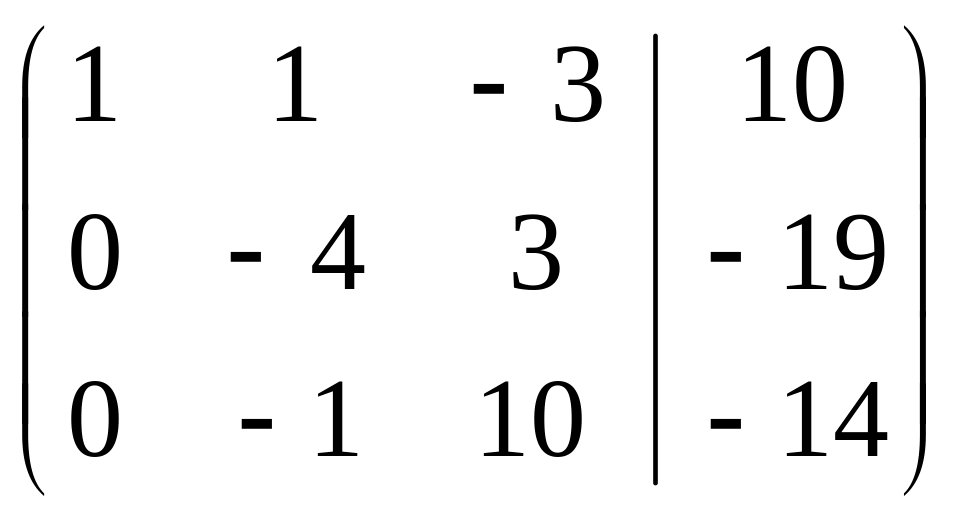 ~ меняем местами 2^ую и 3^ю строки ~ ~ 2^ую строку умножим на -1 ~ 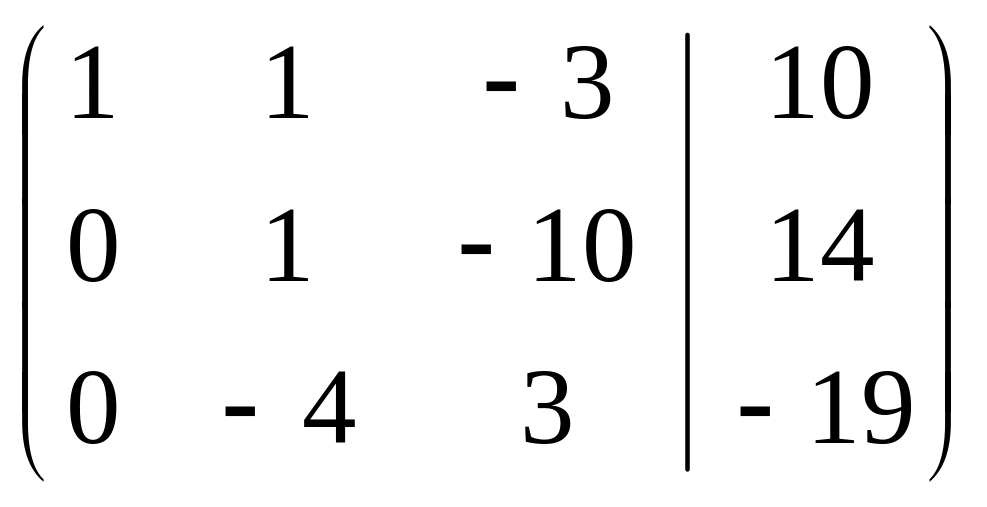~ 3^я строка +2^ая, умноженная на 4 ~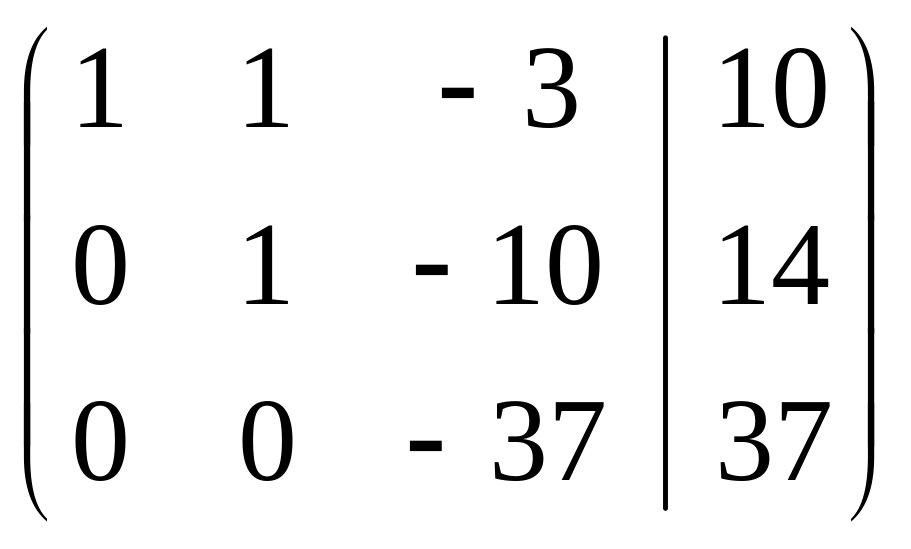 ~ 3^ю строку делим на -37 ~ 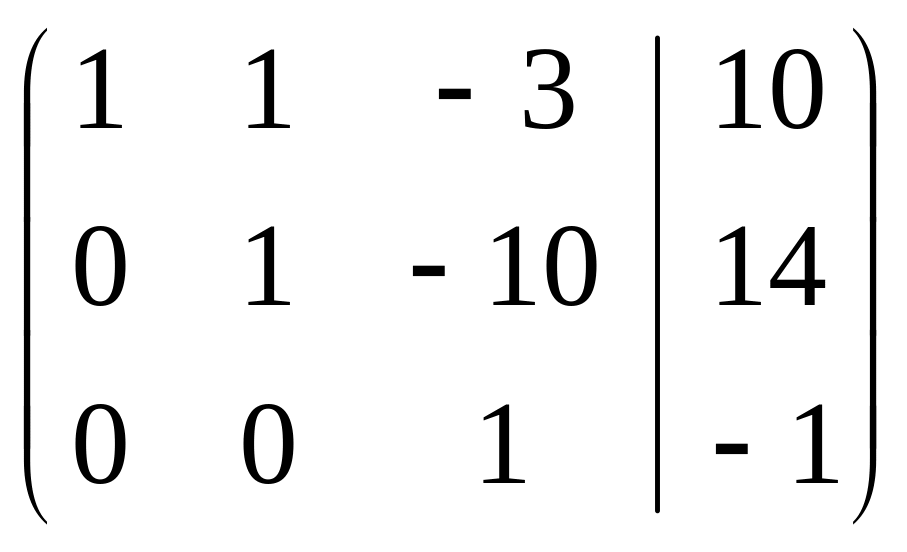~ 2^ая строка +3^я, умноженная на 10; 1^ая строка +3^я, умноженная на 3 ~ 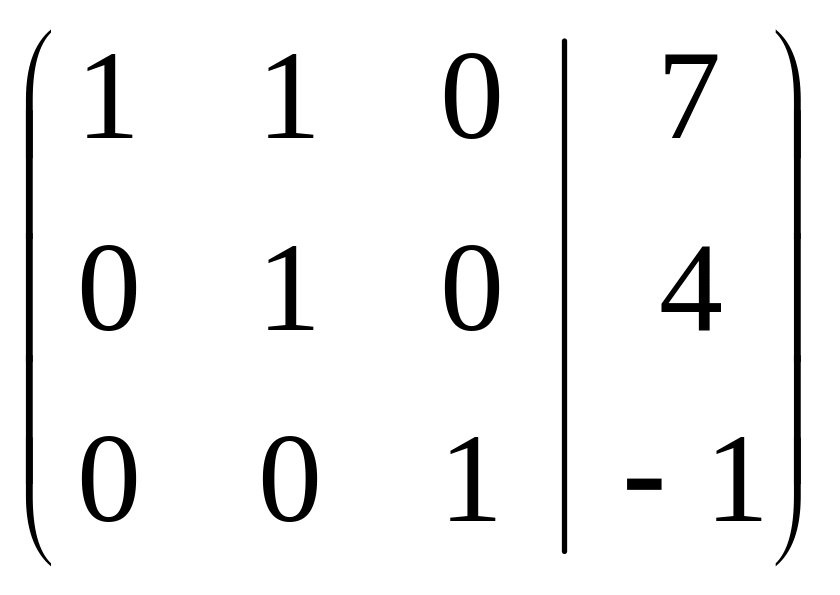~ из 1^ой строки вычитаем 2^ую ~ .

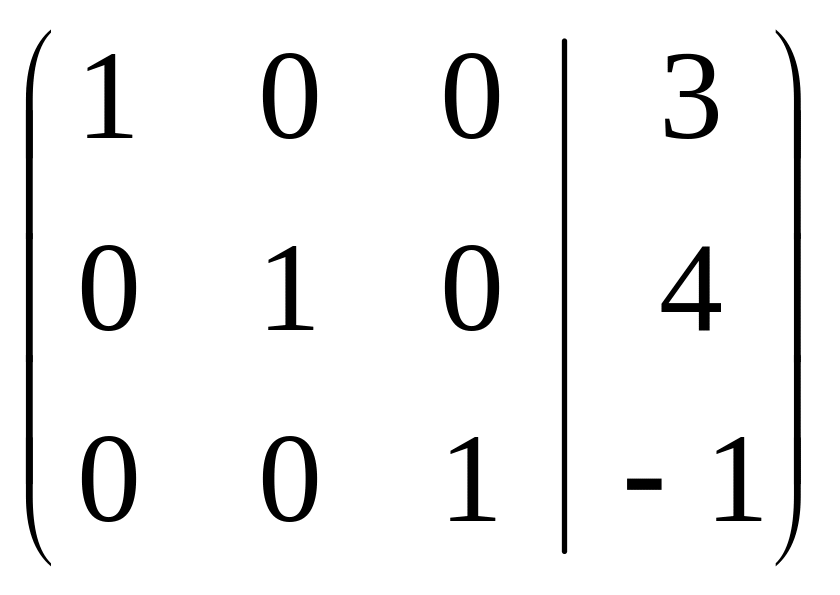Получаем ответ .

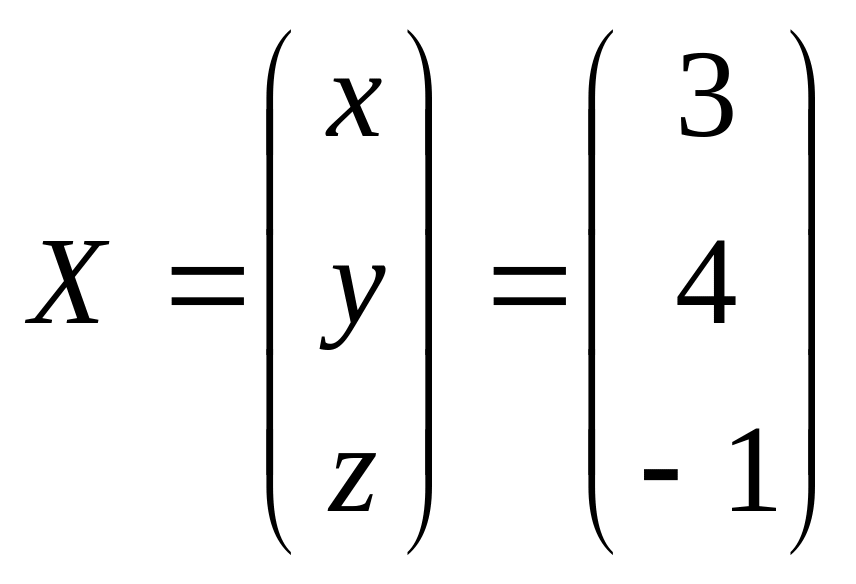Теорема 4.1. (Кронекера-Капелли) Система линейных уравнений совместна, тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы, т.е.

.

Для совместных систем справедливы следующие следствия.

Следствие 1. Если ранг матрицы совместной системы равен числу переменных , то система (14) имеет единственное решение.

Следствие 1. Если ранг матрицы совместной системы меньше числа переменных , то система (14) имеет бесконечное множество решений.

Пусть , переменных называются базисными, если определитель матрицы из коэффициентов при них отличен от нуля. Остальные называются свободными.

Решение системы (14), в котором все свободных переменных равны нулю, называется базисным.