4. Синтез замкнутой оптимальной по быстродействию системы

4.1. Построение функции переключения и фазовой траектории

Реализация разомкнутых систем, оптимальных по быстродействию, затруднительна, когда к управляемому объекту прикладываются внешние возмущающие воздействия, вызывающие необходимость изменения моментов переключения.

21

В замкнутых оптимальных по быстродействию системах возможна коррекция моментов переключения в зависимости от внешних возмущающих воздействий или изменений характеристик управляемого объекта. Рассмотрим синтез замкнутой системы, оптимальной по быстродействию, методом фазовой плоскости на примере управляемого объекта, описываемого уравнением (3.10)

,

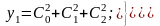откуда

(3.39)

После подстановки (3.39) в (3.26) получим

_(3.40)

Значение y₁ получаем из первого интервала при t = t₁.

Кроме того, найдем при t = t₁ с помощью выражения (3.37)

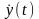
, (3.41)

откуда

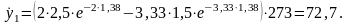
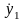
Используя значение и учитывая, что второй интервал времени t=t₂-t₁=0,02 мал, то на основании (3.40) найдем y(t) сразу для t=0,02. В результате получим

20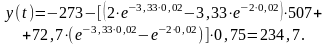

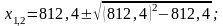
откуда

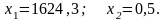
Корень x₂ не является решением системы уравнений (3.18), так как число e в положительной степени больше единицы. Поэтому тогда

На рис. 3.3 графически представлено оптимальное управляющее воздействие, обеспечивающее перевод разомкнутой системы в заданное состояние за минимальное время.

Рис. 3.3

Пример 3.2. С – часть системы описывается уравнением

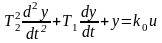, (3.23)

13

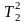где =0,15 с; Т₁=0,8 с; k₀=2,15; ед.

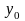
Требуется перевести С – часть системы из положения при t₀ =0 в положение , за минимальное время.

Решение уравнения (3.23) приводит к двум отрицательным вещественным корням, что будет свидетельствовать о двух интервалах максимального управляющего воздействия.

Определим моменты переключения t₁ и отключения t₂ оптимального управляющего воздействия.

Решение (3.23) на первом интервале управления

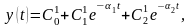(3.24)

где , - постоянные интегрирования на первом интервале управления; ₁ и ₂ - корни характеристического уравнения.

Используя начальные условия при 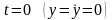найдем постоянные интегрирования:

,

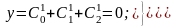откуда получаем

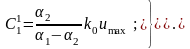(3.25)

Запишем решение уравнения (3.23) на втором интервале управления

(3.26)

где , - постоянные интегрирования на втором интервале.

Используя конечные условия при определим постоянные интегрирования:

,

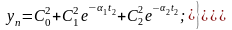откуда получаем

14

Используя данные табл 3.1 и 3.2, строим переходный процесс оптимальной по быстродействию системы (см. рис. 3.4), который необходимо подтвердить модели-рованием на ПЭВМ.

Пример 3.4. Определим движение системы на первом интервале 0<t<t₁, используя решение (3.24) уравнения (3.23) и выражения (3.25) для постоянных интегрирования. С учетом этих равенств получим

, (3.37)

или в иной форме

. (3.38)

После подстановки численных значений параметров в равенство (3.37) запишем

.

Результаты расчетов для t в интервале 0 t t₁ сведены в табл. 3.3.

Таблица 3.3

tc	0	0,2	0,4	0,6	0,8	1,0	1.2	1,38
y(t)	0	25,75	74,29	122,87	163,68	195,27	218,62	233,96

Оптимальный процесс на втором интервале, т.е. в диапазоне времени 0 t t₂ - t₁ описывается уравнением (3.26)

.

19

Принимая момент переключения за начало процесса t = 0, можно записать 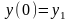и . Тогда

при 0tt. (3.34)

Определим постоянные интегрирования. С этой целью рассмотрим условно момент времени t₁=0. Тогда из (3.34) следуют равенства:

. (3.35)

. (3.36)

Величина y_c соответствует моменту переключения. Значения в (3.35) находятся с помощью уравнений (3.13), в которых вместо t₂ используется t. В результате получаем: 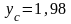ед.

Далее определим величину , используя уравнение (3.14) и рассматривая момент переключения t₁, получим:

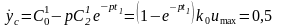ед/c.

Тогда из (3.36) следует

Определяем из (3.35)

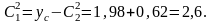
Подставляя в (3.35) численные значения постоянных интегрирования, имеем:

.

Результаты вычислений сведены в табл. 3.2.

Таблица 3.2

t	0	0.1	0.2	0.3	0.4
y(t)	1,98	2,022	2,05	2,07	2,07

Проверим производную в момент времени :

18

Таким образом, условия в конце управления выполняются.

(3.27)

Стыкуем решения на момент времени t₁:

,

или

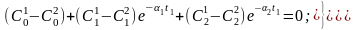. (3.28)

Воспользуемся (3.25) и (3.27), получим:

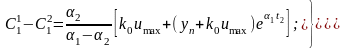. (3.29)

Подставим (3.29) в систему (3.28), получим систему

уравнений для определения моментов переключения

,

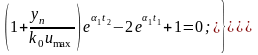15

или

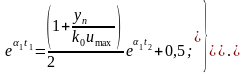(3.30)

Из системы уравнений (3.30) получаем

(3.31)

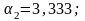
Учитывая численные значения параметров системы (3.31) , получим

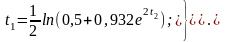(3.32)

Из совместного решения системы уравнений (3.32) находим моменты переключения t₁=1,38 c и t₂=1,4 с.

Далее следует аналогично рассчитать и графически построить зависимости моментов переключения t₁ и отключения t₂ как функций конечного значения y_n вектора состояния для двух промежуточных состояний 0,3 y_n и 0,7 y_n.