
- •Высшая математика
- •Введение
- •Глава I. Неопределенные и определенные интегралы
- •1.Неопределенный интеграл
- •Непосредственное интегрирование.
- •Интегралы вида .
- •Интегралы вида
- •Основные методы вычисления определенных интегралов
- •Формула Ньютона – Лейбница.
- •2.Замена переменной в определенном интеграле.
- •Интегрирование по частям в определенном интеграле.
- •3. Несобственные интегралы
- •4. Приложения определенных интегралов
- •Глава 2. Дифференциальные уравнения
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Дифференциальные уравнения первого порядка Дифференциальные уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка. Уравнение Бернулли
- •3. Дифференциальные уравнения, допускающие понижение порядка Уравнение вида .
- •Уравнение вида .
- •4. Линейные дифференциальные уравнения - го порядка.
- •5. Системы дифференциальных уравнений
- •Глава 3. Дифференциальное исчисление функций многих переменных
- •1. Пискунов н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука, 1989. Т.1,2.
- •2. Щипачев в.С. Высшая математика. М.: Высш. Шк., 1990.
- •1. Основные понятия
- •2. Предел и непрерывность функции
- •Частные производные. Дифференциал функции
- •Производная в данном направлении. Градиент
- •Экстремумы функции нескольких переменных
- •Оглавление
- •Глава I. Неопределенные и определенные интегралы………….…3
- •3. Несобственные интегралы ……………………………………………….15
- •4. Приложения определенных интегралов ………………………………...17
- •Глава II. Дифференциальные уравнения ……………………………...18
- •Глава III. Дифференциальное исчисление функций многих переменных ……………………………………………………………………31
Экстремумы функции нескольких переменных
Говорят, что функция
имеет максимум
(минимум) в
точке
,
если для всех точек
из
-
окрестности точки
выполняется неравенство
![]() (
(
![]() ).
Максимум или минимум функции называется
её экстремумом.
).
Максимум или минимум функции называется
её экстремумом.
Если функция имеет частные производные и точка - точка экстремума функции , то частные производные функции в этой точке равны нулю:
![]() (13)
(13)
(необходимый признак существования экстремума функции двух переменных).
Точки, в которых
![]() и
и
![]() равны нулю или не существуют, называются
критическими.
Таким образом, точки экстремума функции
следует искать среди её критических
точек.
равны нулю или не существуют, называются
критическими.
Таким образом, точки экстремума функции
следует искать среди её критических
точек.
Следующая теорема дает достаточный признак существования экстремума функции двух переменных:
если выполнено условие:
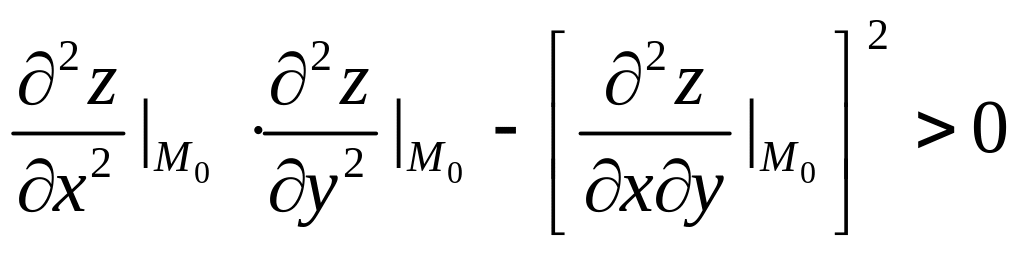 ,
(14)
,
(14)
то в точке
функция
имеет экстремум, причем в случае
![]() точка
- точка максимума, а в случае
точка
- точка максимума, а в случае
![]() точка
- точка минимума;
точка
- точка минимума;
если выполнено условие:
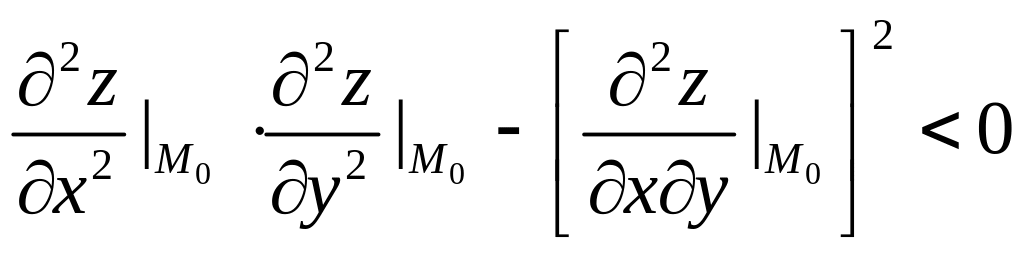 ,
(15)
,
(15)
то у функции нет экстремума в точке ;
если выполнено условие:
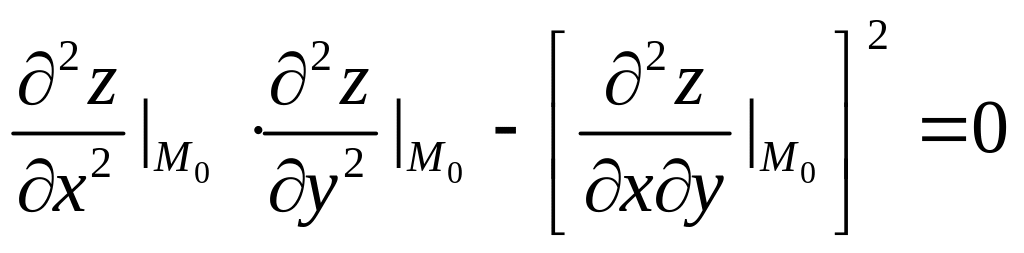 ,
(16)
,
(16)
то вопрос о наличии у функции в точке экстремума остается открытым – требуются дополнительные исследования.
Функция , непрерывная в замкнутой области и дифференцируемая внутри неё, достигает своего наибольшего (наименьшего) значения либо внутри области , либо на её границе.
Нахождение наибольшего и наименьшего значений данной функции рекомендуется проводить по следующей схеме:
Найти критические точки, лежащие внутри области , и вычислить значения функции в этих точках.
Найти наибольшее и наименьшее значения функции на каждой линии, ограничивающей область. Это сводится к нахождению наибольшего и наименьшего значений функции одной переменной.
После этого среди всех полученных значений найти наибольшее наименьшее. Эти значения и будут соответственно наибольшим и наименьшим значениями функции в замкнутой области .
Задание.
Найти
наибольшее и наименьшее значения функции
![]() в замкнутой области
,
ограниченной прямой
и параболой
.
в замкнутой области
,
ограниченной прямой
и параболой
.
Решение. 1. Сделаем чертеж области :
2. Найдем критические точки данной функции , лежащие внутри области . Для этого найдем частные производные функции и приравняем их к нулю:
![]() ,
,
![]()
Решением системы является значения:
![]()
Точка
![]() не принадлежит замкнутой области
.
Следовательно, наибольшее и наименьшее
значения данная функция
может принимать только на границе
области
.
не принадлежит замкнутой области
.
Следовательно, наибольшее и наименьшее
значения данная функция
может принимать только на границе
области
.
3. Исследуем функцию на границе области .
1) На отрезке прямой имеем функцию
![]() ,
,
которая представляет
собой функцию одной переменной
![]() .
Её наибольшее и наименьшее значения
следует искать среди её значений в
критических точках и на концах отрезка
.
Её наибольшее и наименьшее значения
следует искать среди её значений в
критических точках и на концах отрезка
![]() .
Найдём производную функции
и приравняем её к нулю:
.
Найдём производную функции
и приравняем её к нулю:
![]() .
.
Решая полученное уравнение, находим:
![]()
- критическая
точка, но она не принадлежит отрезку
![]() .
Следовательно, наибольшее и наименьшее
значения функция
принимает на концах отрезка
:
.
Следовательно, наибольшее и наименьшее
значения функция
принимает на концах отрезка
:
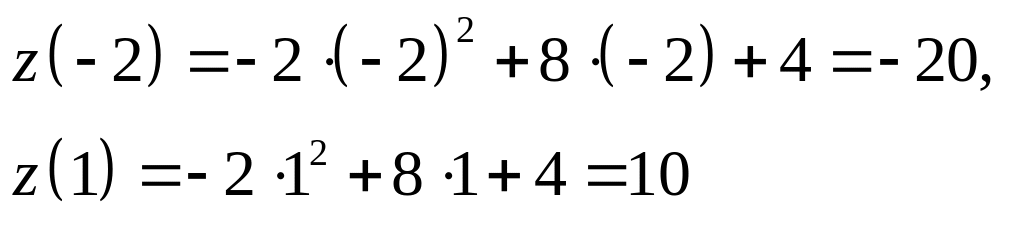
2) На дуге параболы имеем функцию
![]() ,
,
которая представляет собой функцию одной переменной . Найдем производную функции и приравняем к нулю:
![]() .
.
Решая полученное уравнение, находим его корни:
![]()
- критические
точки, из которых только значение
![]() принадлежит отрезку
.
Следовательно, наибольшее и наименьшее
значения функция
принимает либо в точке
,
либо на концах отрезка
:
принадлежит отрезку
.
Следовательно, наибольшее и наименьшее
значения функция
принимает либо в точке
,
либо на концах отрезка
:
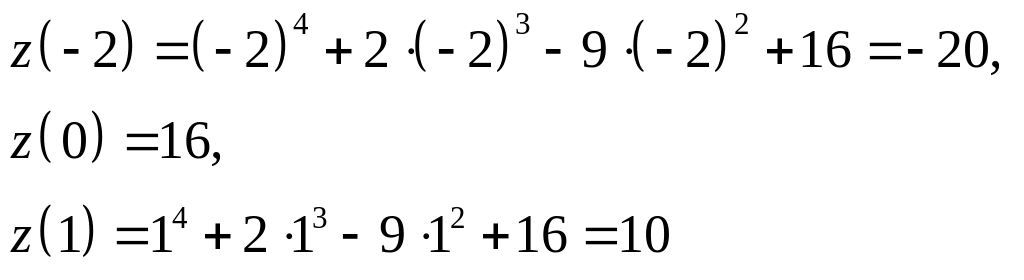
Сравнивая все
вычисленные значения функции
,
находим наибольшее и наименьшее значения
данной функции в замкнутой области
:
![]() -
наибольшее значение (в точке
-
наибольшее значение (в точке
![]() );
);
![]() - наименьшее значение (в точке
- наименьшее значение (в точке
![]() ).
).
Контрольная работа № 4
Неопределенные и определенные интегралы
Задание 1. Найти неопределенные интегралы.
а)
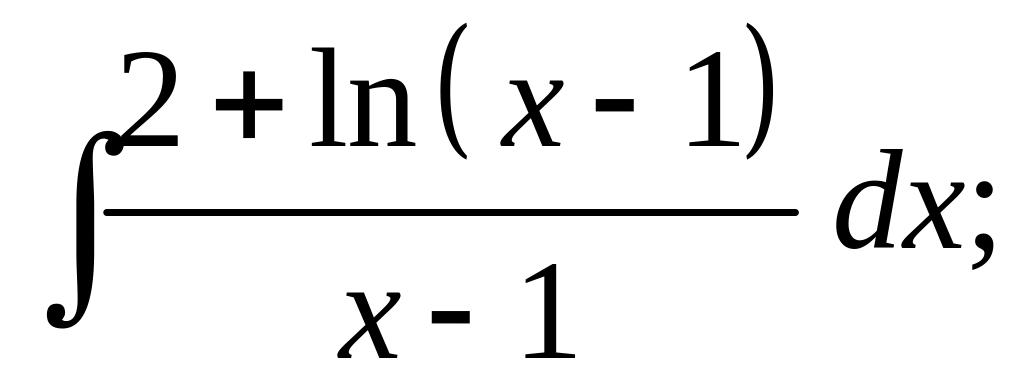 б)
б)
 в)
в)
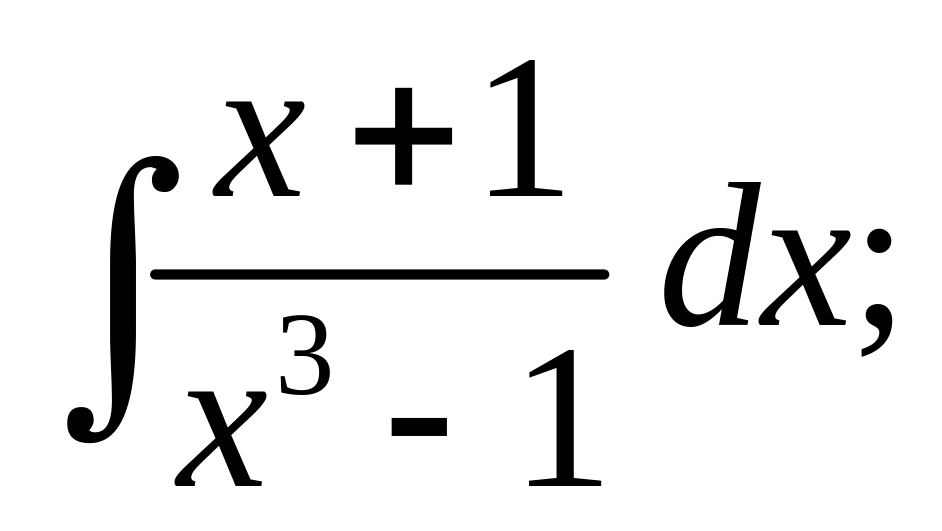 г)
г)
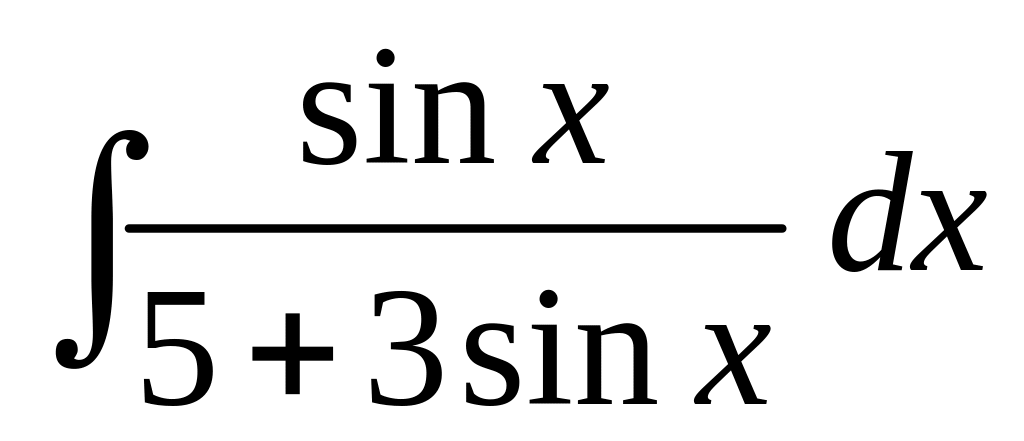
а)
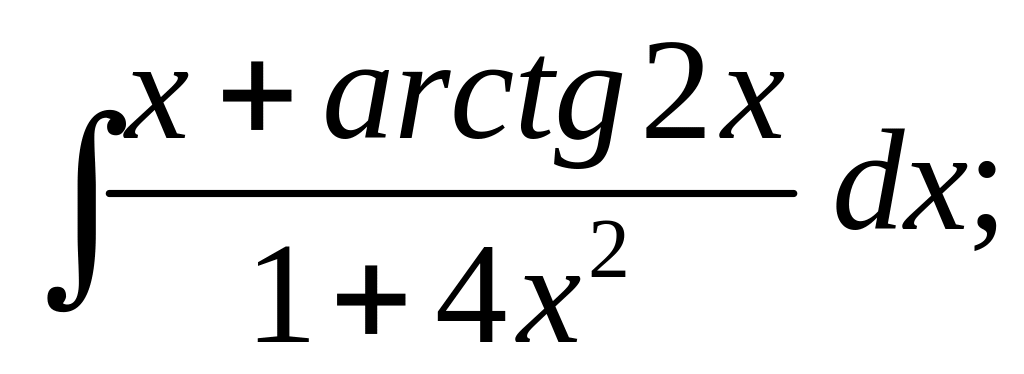 б)
б)
 в)
в)
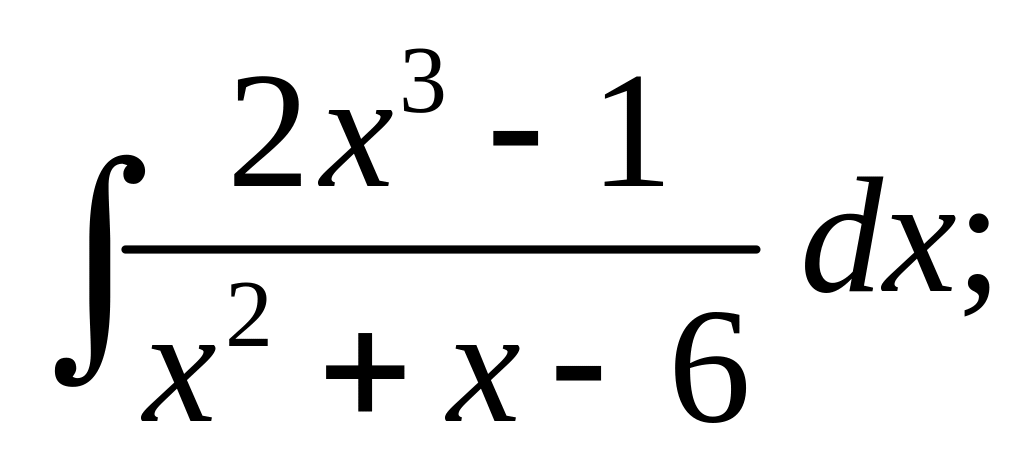 г)
г)
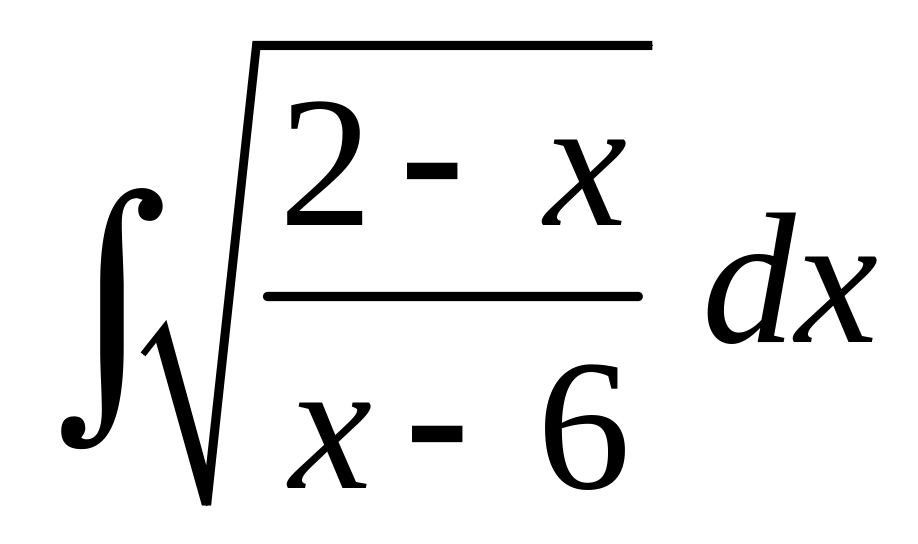
3. а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
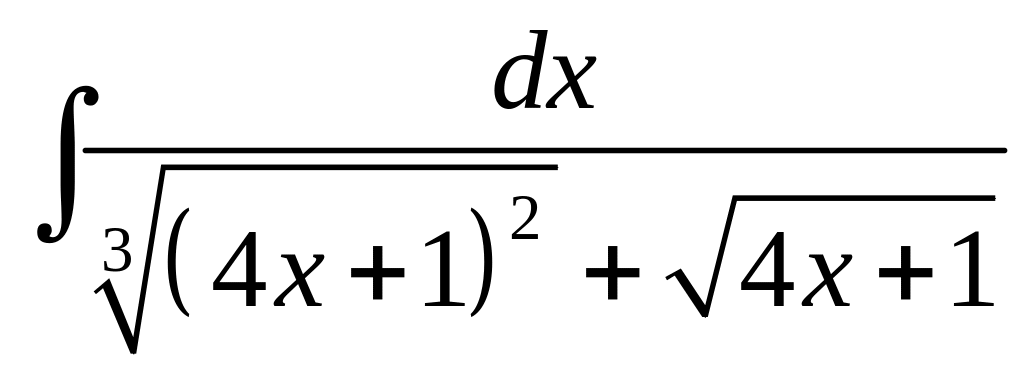
4. а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
5. а)
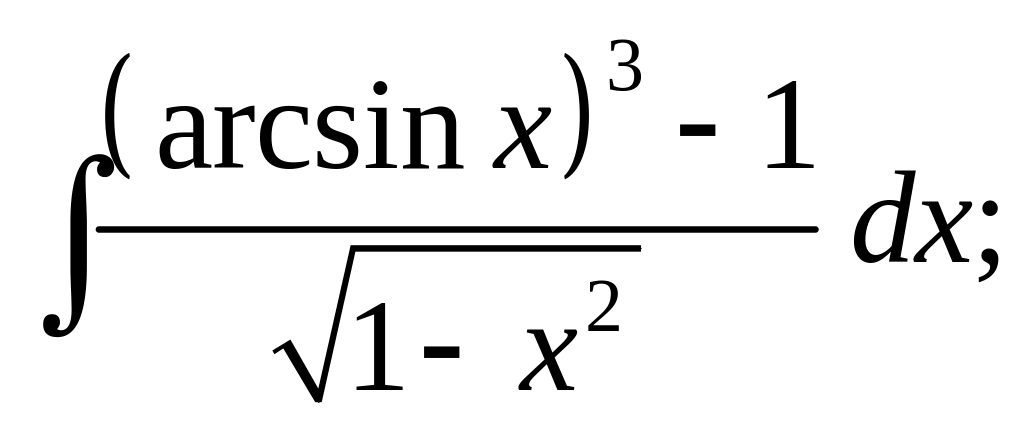 б)
б)
![]() в)
в)
![]() г)
г)
![]()
6. а)
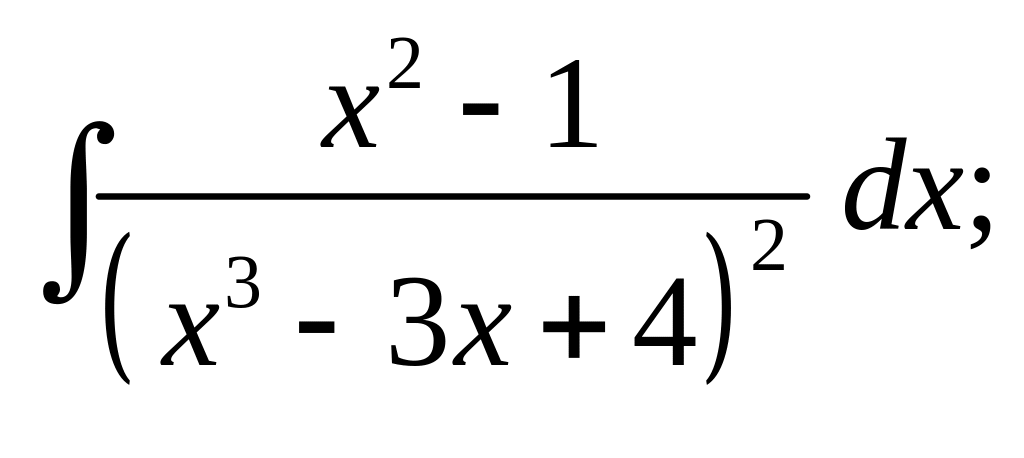 б)
б)
![]() в)
в)
![]() г)
г)
7. а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
8. а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
9. а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
10. а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
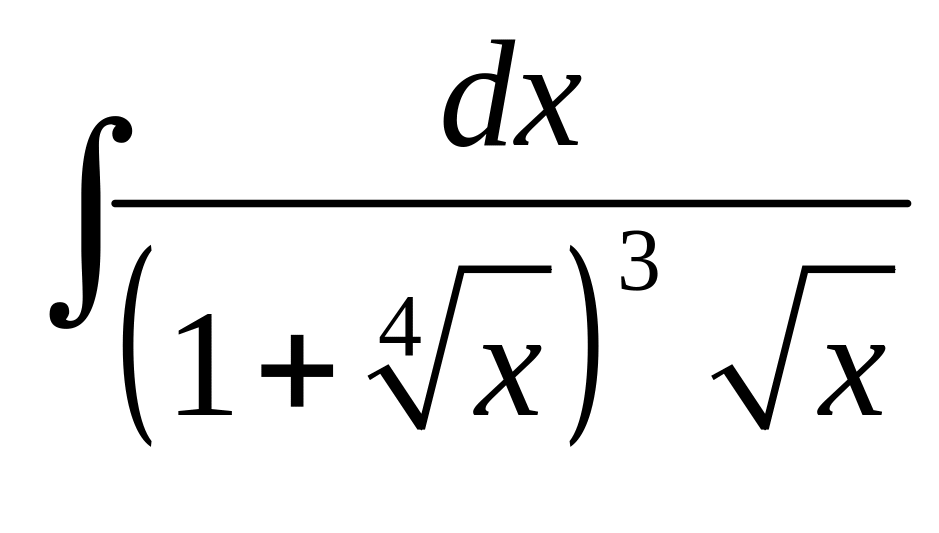
Задание 2. Вычислить определенные интегралы.
1.
а)
![]() б)
б)
![]()
2.
а)
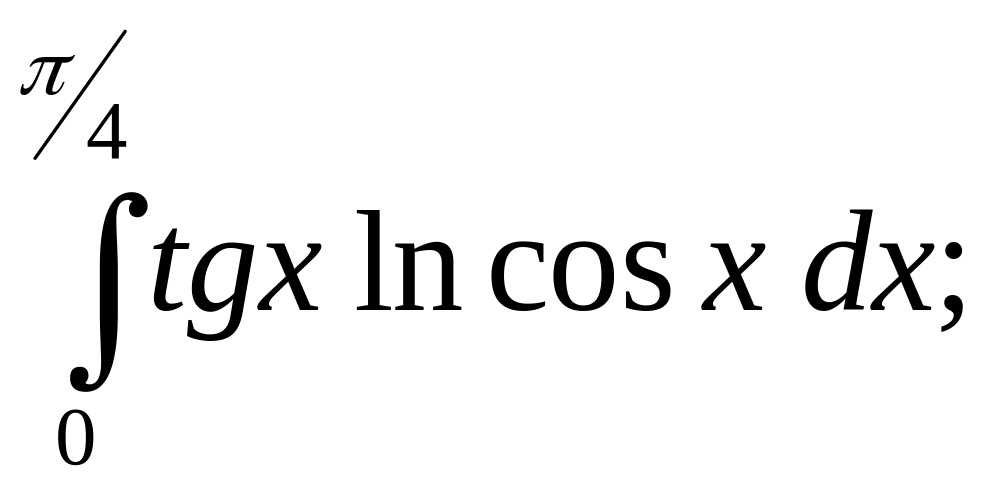 б)
б)
![]()
3.
а)
![]() б)
б)
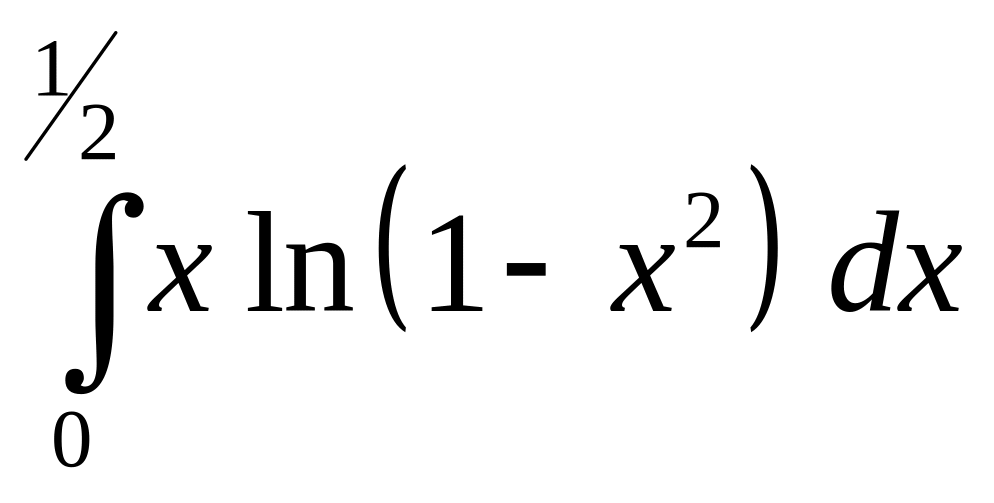
4.
а)
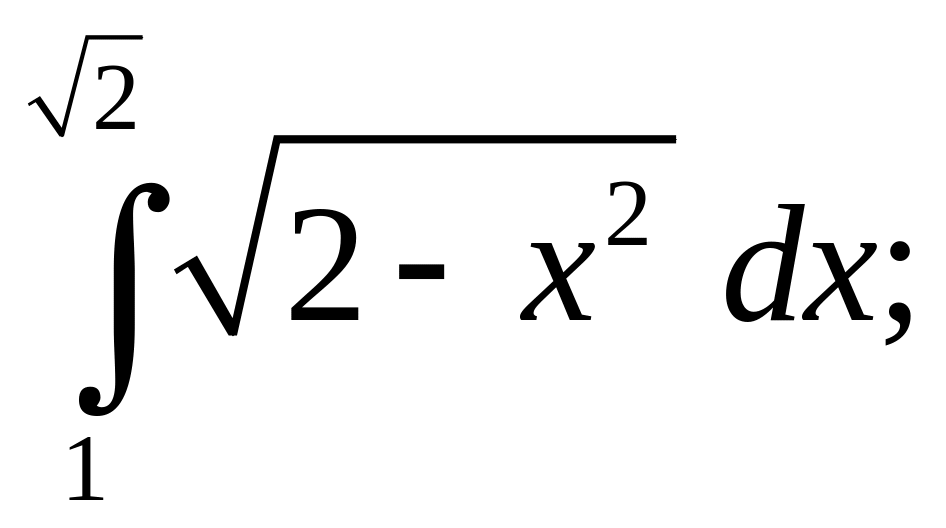 б)
б)
![]()
5.
а)
![]() б)
б)
![]()
6.
а)
![]() б)
б)
![]()
7.
а)
![]() б)
б)
![]()
8.
а)
![]() б)
б)

9.
а)
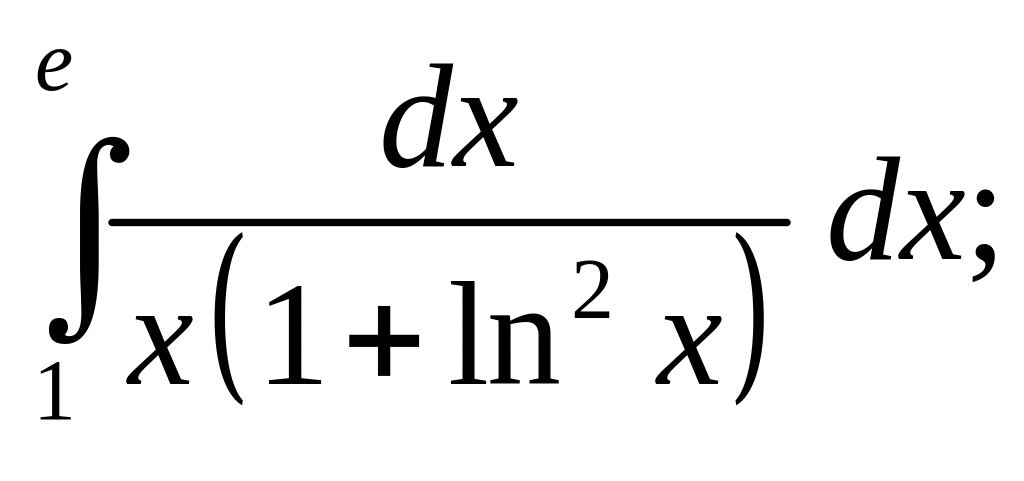 б)
б)
![]()
10.
а)
![]() б)
б)
![]()
Задание 3. Вычислить несобственные интегралы (или установить их расходимость).
1.
![]() 2.
2.
![]()
3.
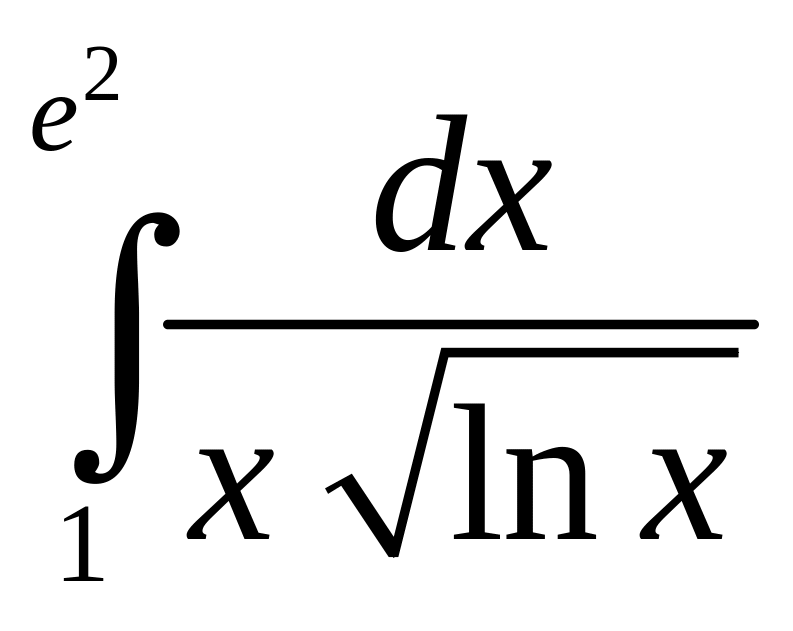 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
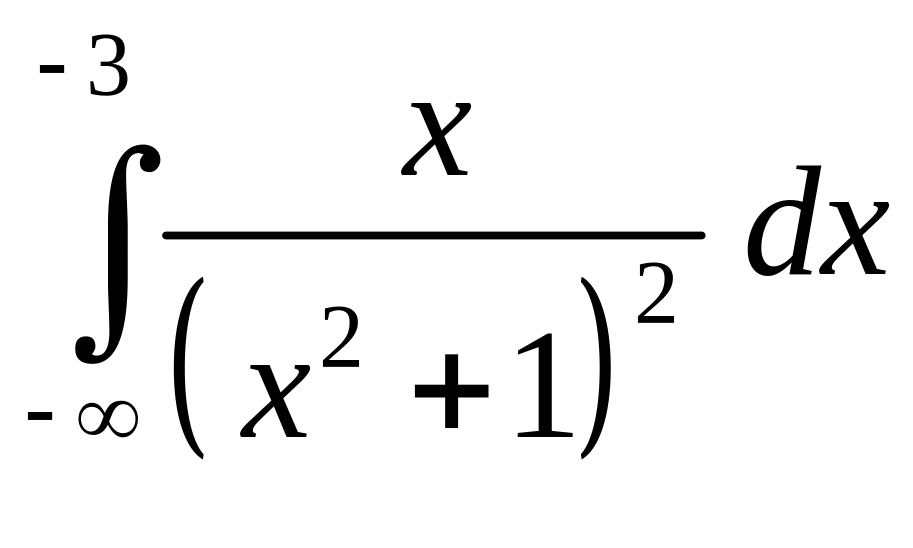 10.
10.
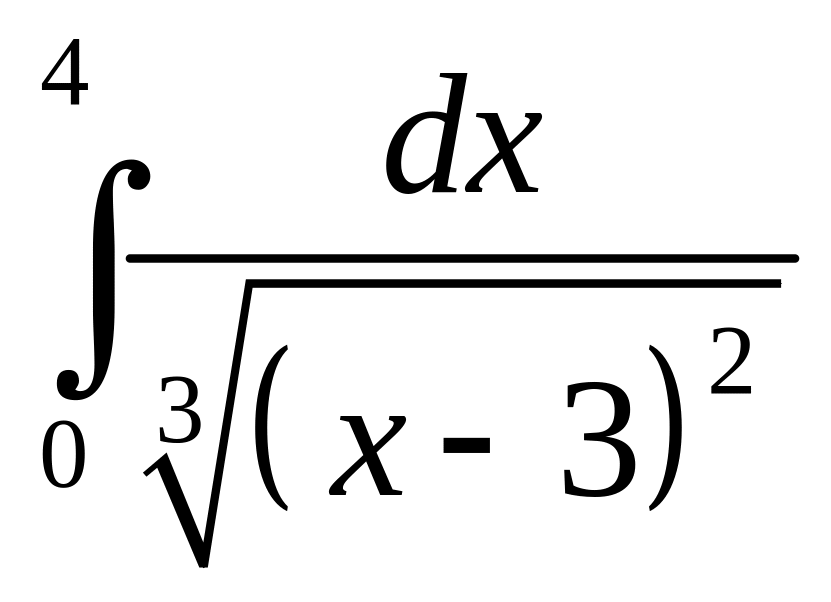
Задание 4 .
1. Вычислить площадь
фигуры, ограниченной кривыми
и
![]() .
.
2. Найти площадь
фигуры, ограниченной одной аркой циклоиды
![]() и осью
.
и осью
.
3. Найти длину дуги
параболы
![]() от
до
.
от
до
.
4.Найти длину
астроиды
![]() .
.
5. Найти площадь
поверхности, образованной вращением
вокруг оси
дуги кривой
![]() от
от
![]() до
.
до
.
6. Найти площадь
поверхности, образованной вращением
одной арки циклоиды
![]() вокруг оси
.
вокруг оси
.
7. Найти объём тела,
образованного вращением вокруг оси
фигуры, ограниченной линиями
![]() и
и
![]() .
.
8. Вычислить длину
кардиоиды
![]() .
.
9. Найти площадь
фигуры, ограниченной кардиоидой
![]() .
.
10. Найти площадь
фигуры, ограниченной кривыми
![]() и
и
![]() .
.
Контрольная работа № 5
Дифференциальные уравнения
Задание 1. Найти общие решения уравнений.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
Задание 2. Найти общие решения уравнений.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.![]() 10.
10.
![]()
Задание 3. Найти решения задач Коши.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.
![]()
Задание 4. Методом вариации произвольных постоянных решить уравнения.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
Задание 5. Найти общие решения систем уравнений.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
Контрольная работа № 6
Дифференциальное исчисление функций нескольких переменных
Задание 1.
Дана функция
![]()
Показать, что
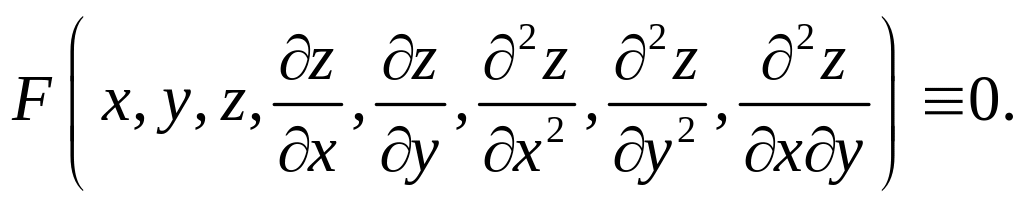
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]() 7.
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
Задание 2.
Даны функции
![]() и
и
![]() ,
точка
и вектор
.
Найти:
,
точка
и вектор
.
Найти:
а) угол
между grad![]() и grad
и grad![]() в точке
в точке
![]()
1.
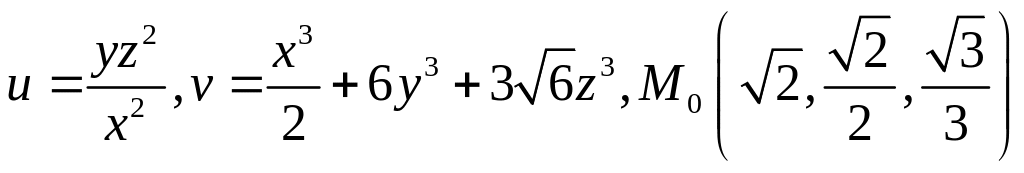
2.
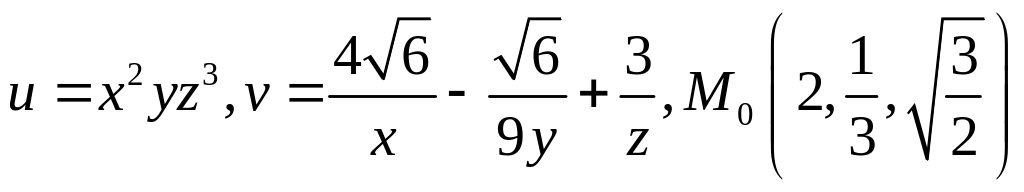
3.
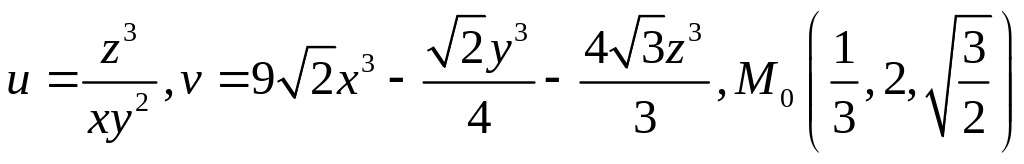
4.
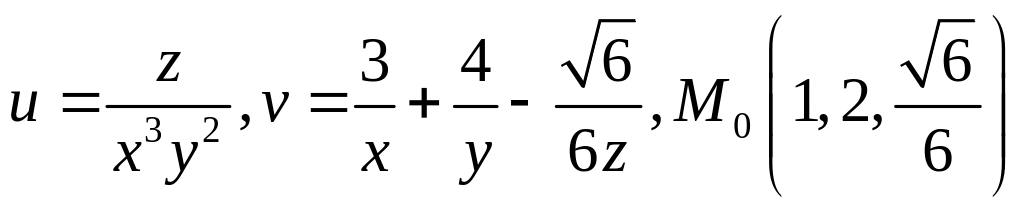
5.
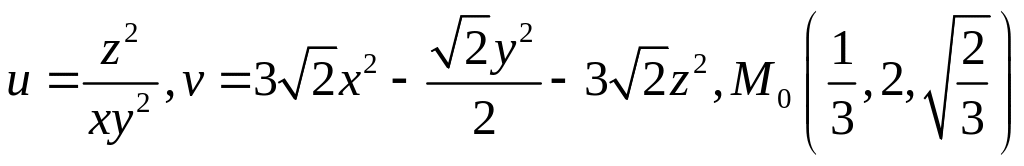
б) производную в точке по направлению вектора :
6.
![]()
7.
![]()
8.![]()
9.
![]()
10.
![]()
Задание 3. Составить уравнения касательной плоскости и нормали к поверхности в точке :
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
Задание 4. Найти наименьшее и наибольшее значения функции в замкнутой области , заданной системой неравенств. Сделать чертеж.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
