5. Підготовка до самостійної роботи № 5.

Для підготовки до самостійної роботи № 5 необхідно розв’язати наступні задачі:

1) Привести рівняння кола до канонічного, знайти центр і радіус, зобразити коло: .

2) Знайти координати фокусів, довжини осей, ексцентриситет еліпса, заданого рівнянням .

3) Знайти координати фокусів, довжини осей, ексцентриситет та рівняння асимптот гіперболи, заданої рівнянням .

Відповіді:

1) ,

2)

3)

6. Виконання другої частини семестрового завдання.

Правила оформлення семестрового завдання дані у вступі даного методичного посібника. Згідно свого варіанту виконайте завдання другої частини, які вказані на сторінці .

Вказівки до виконання семестрового завдання (частина 1)

Завдання 1. Для обчислення визначника четвертого порядку необхідно використати теорему про розкладання визначника по елементах рядка або стовпця:

Сума добутків елементів будь-якого рядка (або стовпця) визначника на їх алгебраїчні доповнення дорівнює цьому визначнику, тобто:

або

.

Приклад 1. Обчислити визначник:

.

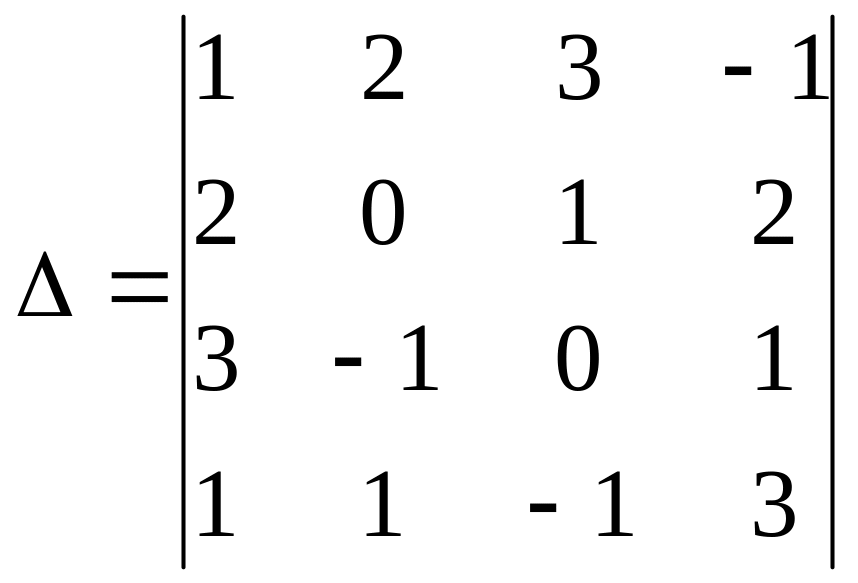Розв’язання. Розкладемо визначник по третьому стовпцю:

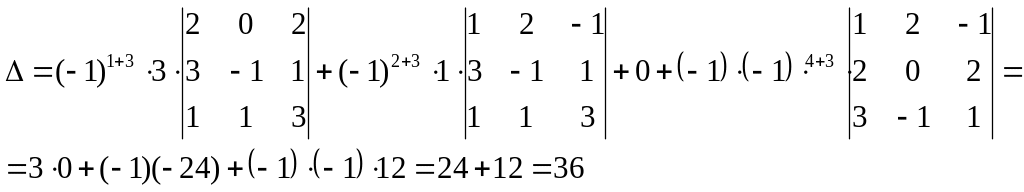
Визначники третього порядку знайдемо окремо.

За правилом трикутників знайдемо перші два визначника у розкладанні:

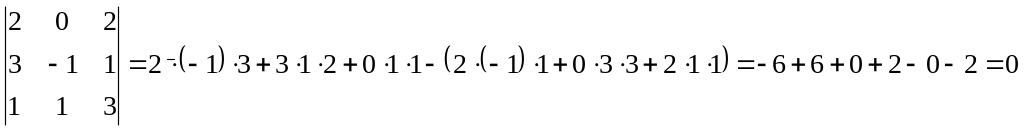
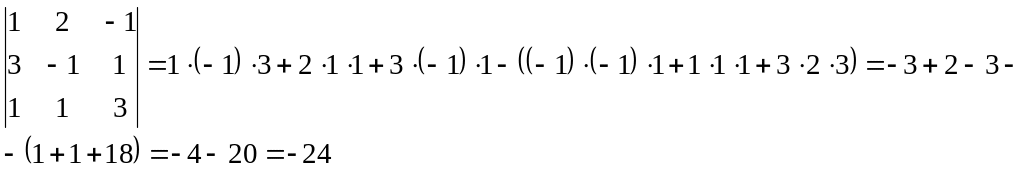Третій визначник розкладемо за другим стовпцем:

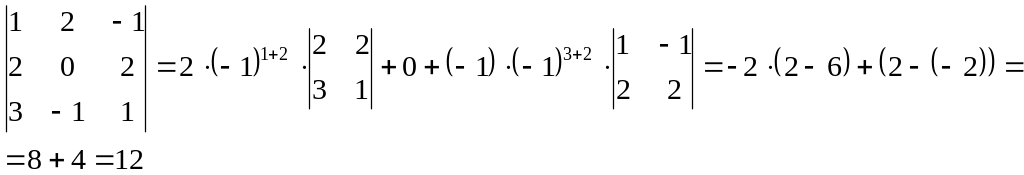
Завдання 2. Розглянемо розв’язання систем лінійних рівнянь трьома методами.

Метод Крамера.

Розв’язання. Обчислимо головний визначник системи та допоміжні визначники , , .

.

; ; .

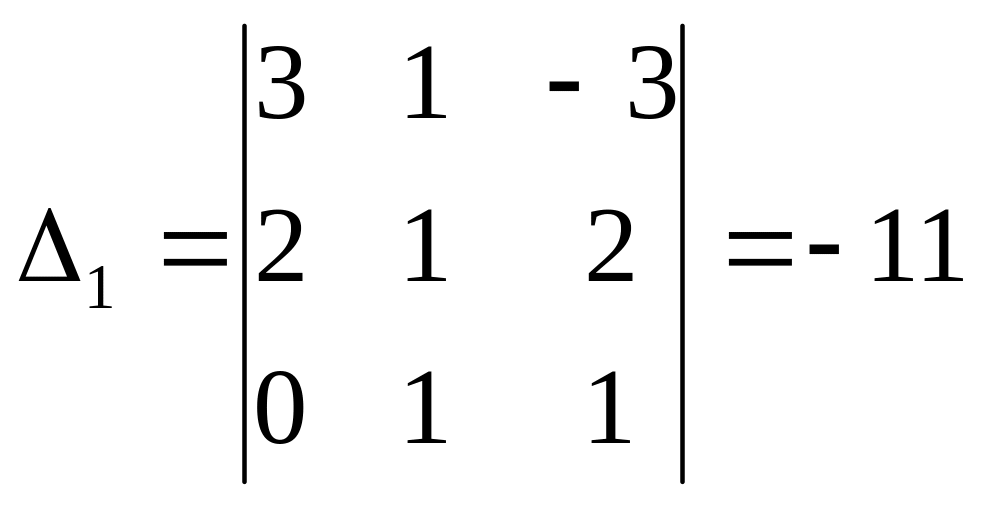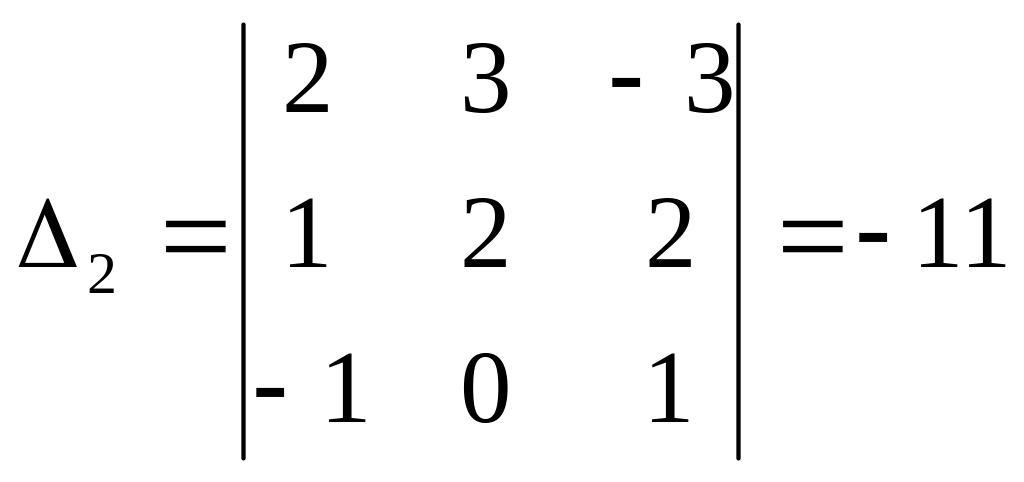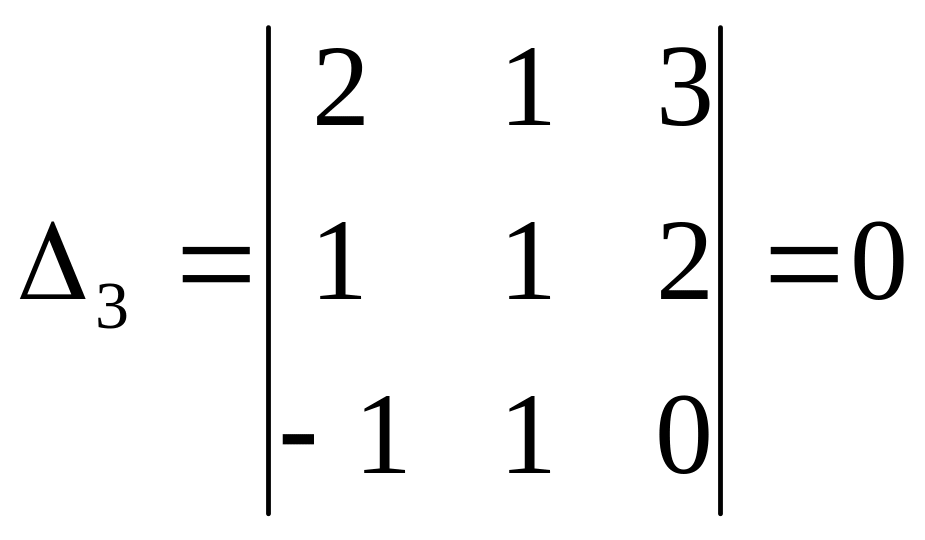За формулами Крамера, отримаємо

; ; .

Відповідь: (1; 1; 0).

Якщо визначник системи дорівнює нулю.

1. і кожний визначник . Це має місце тільки тоді, коли коефіцієнти при невідомих пропорційні, тобто кожне рівняння системи виходить з першого рівняння множенням обох його частин на число . Очевидно, що при цьому система має нескінченну кількість розв’язків.

2. і хоча б один з визначників . Це має місце тільки тоді, коли коефіцієнти при невідомих, крім , пропорційні. При цьому виходить система з суперечливих рівнянь, яка не має розв’язку.

Метод Гаусу.

Приклад 1.

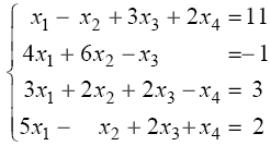
Розв’язання.

У цієї системи коефіцієнт відмінний від нуля. Якщо б ця умова не виконувалась, то необхідно було б переставити місцями рівняння, поставивши першим те рівняння, в якому коефіцієнт при не дорівнює нулю.

Зробимо наступні перетворення:

1. оскільки 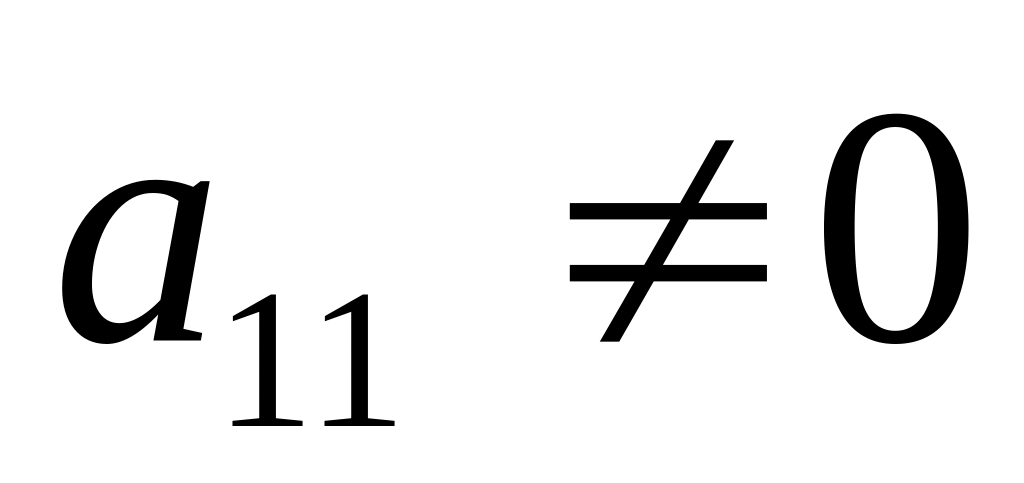, перше рівняння запишемо без змін;

2. замість другого рівняння запишемо рівняння, яке отримується, якщо з другого рівняння відняти перше, помножене на 4;

3. замість третього рівняння запишемо різницю третього і першого, помноженого на 3;

4. замість четвертого рівняння запишемо різницю четвертого і першого, помноженого на 5.

Отримана нова система еквівалентна початковій і має у всіх рівняннях, крім першого, нульові коефіцієнти при (це було метою перетворення):

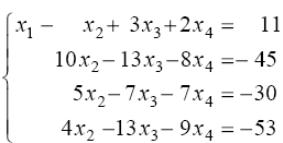
Для приведення наступних перетворень не потрібно записувати всю систему, як це було зроблено. Запишемо розширену матрицю початкової системи:

Після перетворень отримали таку розширену матрицю:

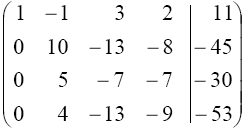
Перетворимо цю матрицю наступним способом:

1. оскільки , перші два рядка залишимо без змін;

2. замість третього рядка запишемо різницю між другим та подвоєним третім;

3. замість четвертого рядка запишемо різницю між подвоєним другим рядком та помноженим на 5 четвертим.

У результаті отримали матрицю, в якій невідома виключена з усіх рівнянь, крім першого, а невідома – з усіх рівнянь, крім першого та другого:

Тепер виключаємо невідому з четвертого рівняння. Для цього останню матрицю перетворимо так:

1. оскільки 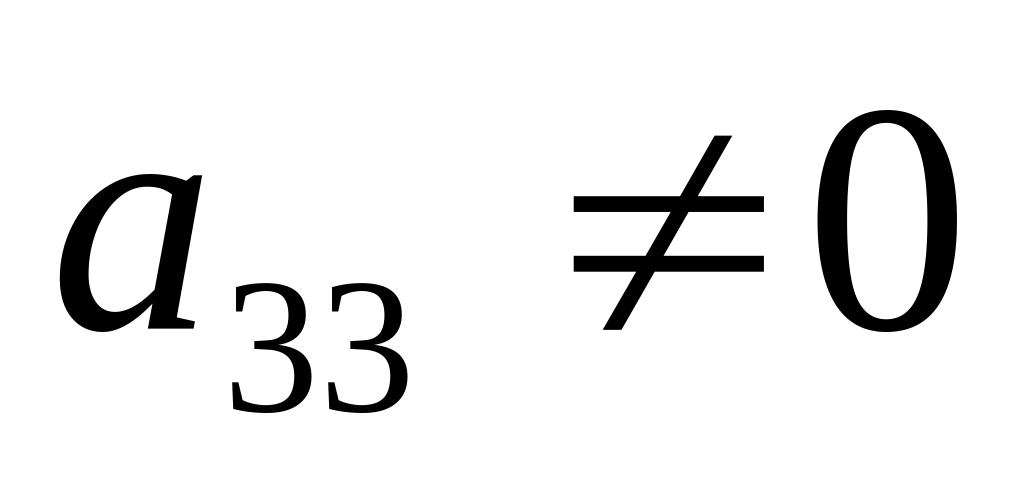, перші три рядки залишимо без змін;

2. замість четвертого рядка запишемо різницю між третім, помноженим на 39, і четвертим:

Отримана матриця відповідає системі:

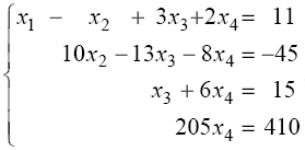
З останнього рівняння цієї системи отримаємо . Підставимо це значення у третє рівняння, отримаємо . Тепер з другого рівняння випливає, що , а з першого – .

Приклад 2.

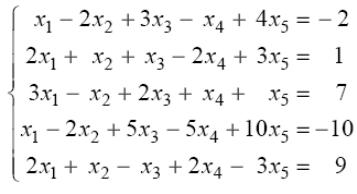
Розв’язання.

Зробимо наступні перетворення розширеної матриці системи:

1. перше рівняння запишемо без змін;

2. замість другого рядка запишемо різницю між другим рядком і подвоєним першим;

3. замість третього рядка запишемо різницю між третім рядком і подвоєним першим;

4. четвертий рядок замінимо різницею між четвертим і першим;

5. п’ятий рядок замінимо різницею між п’ятим і подвоєним першим.

У результаті перетворень отримали матрицю:

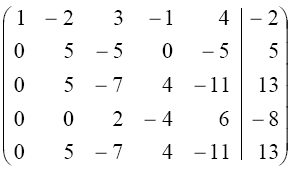
Залишаємо перші два рідка цієї матриці без змін, приводимо її елементарними перетвореннями до наступного виду:

За допомогою третього рядка приводимо до нуля коефіцієнти при у четвертому і п’ятому рядках. Далі поділимо всі елементи другого рядка на 5, а всі елементи третього рядка на 2, отримаємо матрицю:

Два останні рядка матриці відповідають рівнянню Це рівняння задовольняє будь-якому набору чисел , його потрібно видалити з системи. Таким чином, система отриманої розширеної матриці еквівалентна системі з розширеною матрицею виду:

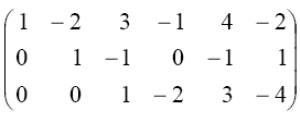
Останній рядок матриці відповідає рівнянню . Якщо невідомим та задати довільні значення: , то з останнього рівняння системи, отримаємо . Підставивши значення , та у друге рівняння, отримаємо . Тепер з першого рівняння можна отримати . Отже, розв’язання системи має вид:

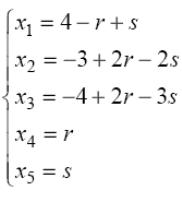
Приклад 3.

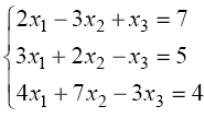
Робимо перетворення:

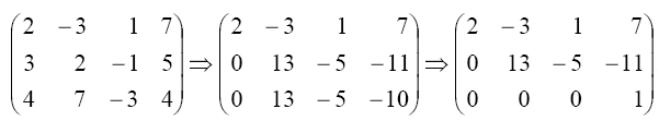
Останній рядок матриці відповідає рівнянню , яке не має розв’язків. Отже, початкова система не має розв’язків.

Висновок:

Якщо при використанні елементарних перетворень до системи рівнянь, хоча б одне рівняння приводиться до виду:

то система несумісна або суперечлива, бо жоден набір чисел не задовольняє цьому рівнянню.

Матричний метод.

Розв’язання.

Матриця коефіцієнтів при невідомих має вигляд:

,

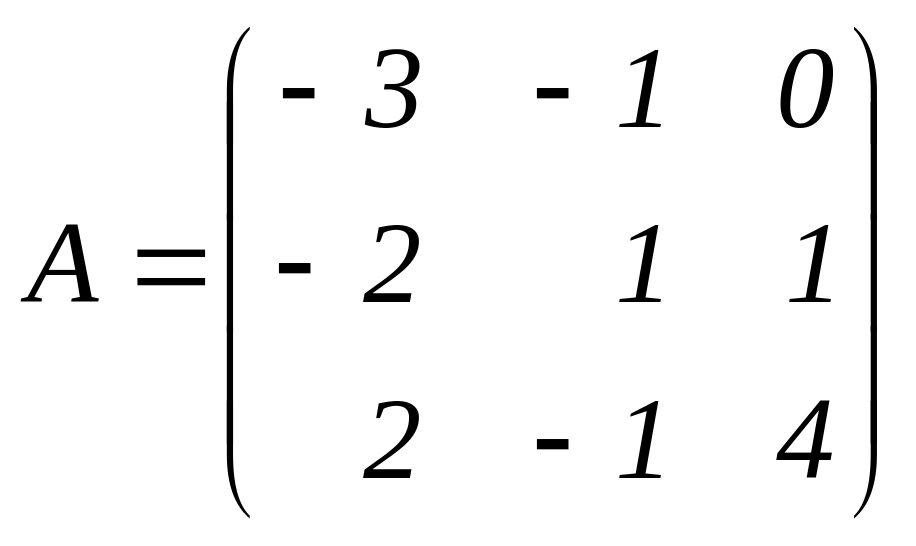матриця невідомих:

,

та матриця вільних членів

.

По-перше, щоб розв’язати систему лінійних рівнянь матричним методом, треба знайти оберну матрицю до матриці .

1. Знайдемо визначник.

.

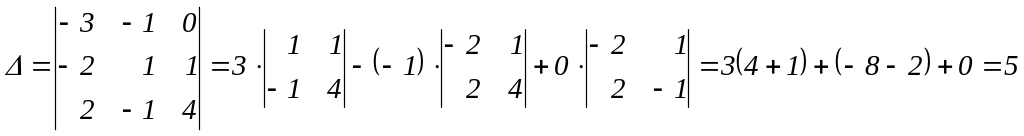, значить, обернена матриця існує.

2. Найдемо алгебраїчні доповнення до кожного з елементів матриці .

.

Запишемо нову матрицю, яка буде складатися з алгебраїчних доповнень.

.

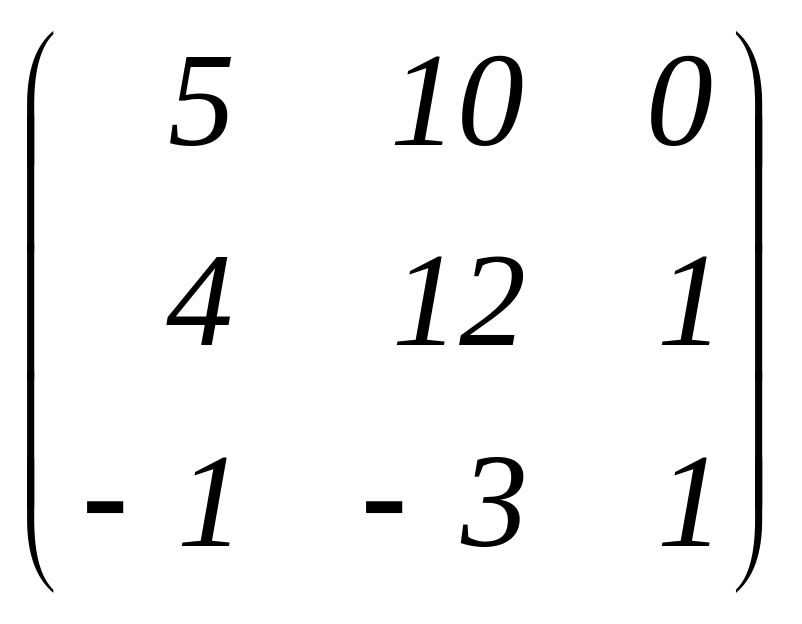3. Транспонуємо отриману матрицю.

.

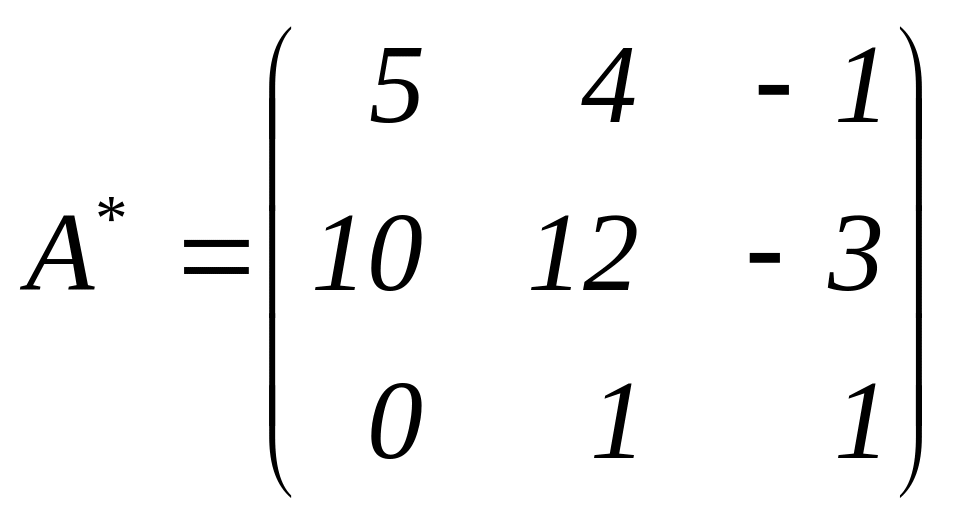4. Помножимо останню матрицю на ,отримаємо обернену матрицю.

.

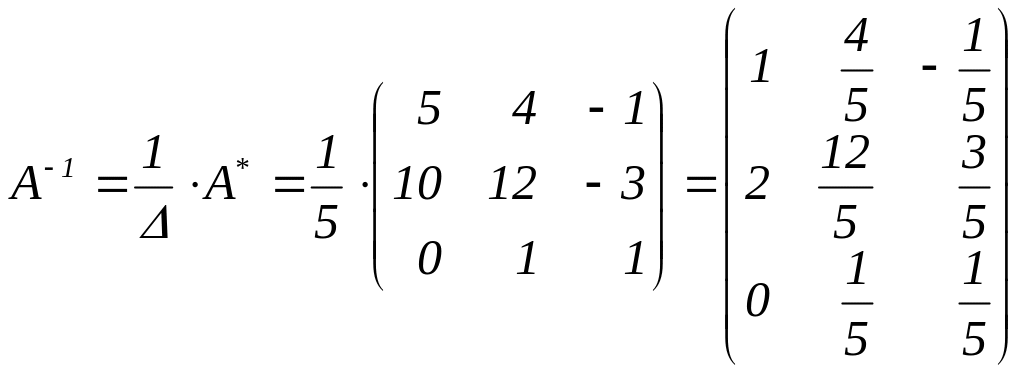По-друге, скористаємося формулою для знаходження невідомих.

.

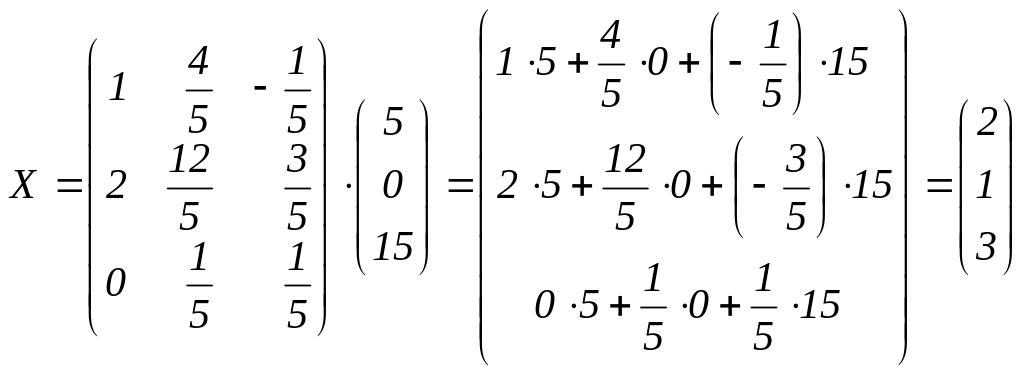Отже, .

Відповідь: .

Завдання 3. Перевіримо на колінеарність вектори й , побудовані по векторах й ?

Розв’язання.

1 спосіб. Вектори колінеарні, якщо їхні відповідні координати пропорційні.

Спочатку знаходимо координати векторів й :

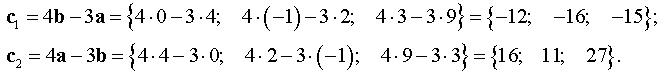
Маємо,

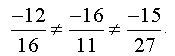
Отже, вектори й неколінеарні.

2 спосіб. Вектори колінеарні, якщо їхній векторний добуток дорівнює нулю.

Аналогічно, знаходимо координати векторів й :

Обчислюємо векторний добуток:

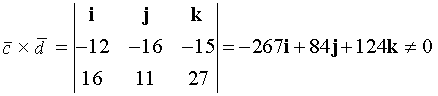
Отже, вектори й неколінеарні.

Завдання 4. Знайти косинус кута між векторами й :

Розв’язання. Косинус кута між векторами й знаходять за формулою:

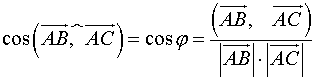
Для обчислення координат векторів використовуємо формули:

;

.

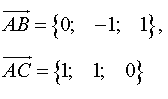
Довжини векторів обчислимо так:

;

.

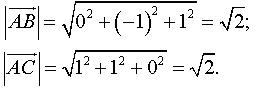
Маємо,

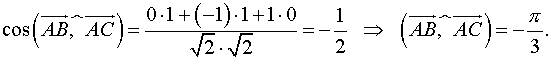
Завдання 5. Обчислити площу паралелограма, побудованого на векторах й , якщо кут між векторами й дорівнює :

Розв’язання. Площа паралелограма дорівнює модулю векторного добутку векторів й :

.

Обчислюємо векторний добуток , використовуючи його властивості:

.

Завдання 6. Перевірити вектори , і на компланарність:

Розв’язання.

Вектори компланарні(лежать на одній площині або на паралельних площинах), якщо їхній мішаний добуток дорівнює .

Знаходимо мішаний добуток за формулою:

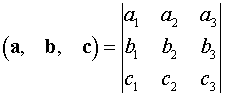
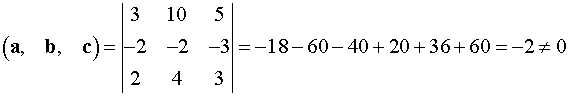
Робимо висновок, що вектори , і не компланарні.